Young Lee
Causal Policy Learning in Reinforcement Learning: Backdoor-Adjusted Soft Actor-Critic
Jun 05, 2025Abstract:Hidden confounders that influence both states and actions can bias policy learning in reinforcement learning (RL), leading to suboptimal or non-generalizable behavior. Most RL algorithms ignore this issue, learning policies from observational trajectories based solely on statistical associations rather than causal effects. We propose DoSAC (Do-Calculus Soft Actor-Critic with Backdoor Adjustment), a principled extension of the SAC algorithm that corrects for hidden confounding via causal intervention estimation. DoSAC estimates the interventional policy $\pi(a | \mathrm{do}(s))$ using the backdoor criterion, without requiring access to true confounders or causal labels. To achieve this, we introduce a learnable Backdoor Reconstructor that infers pseudo-past variables (previous state and action) from the current state to enable backdoor adjustment from observational data. This module is integrated into a soft actor-critic framework to compute both the interventional policy and its entropy. Empirical results on continuous control benchmarks show that DoSAC outperforms baselines under confounded settings, with improved robustness, generalization, and policy reliability.
Benchmarking Robustness of Contrastive Learning Models for Medical Image-Report Retrieval
Jan 15, 2025



Abstract:Medical images and reports offer invaluable insights into patient health. The heterogeneity and complexity of these data hinder effective analysis. To bridge this gap, we investigate contrastive learning models for cross-domain retrieval, which associates medical images with their corresponding clinical reports. This study benchmarks the robustness of four state-of-the-art contrastive learning models: CLIP, CXR-RePaiR, MedCLIP, and CXR-CLIP. We introduce an occlusion retrieval task to evaluate model performance under varying levels of image corruption. Our findings reveal that all evaluated models are highly sensitive to out-of-distribution data, as evidenced by the proportional decrease in performance with increasing occlusion levels. While MedCLIP exhibits slightly more robustness, its overall performance remains significantly behind CXR-CLIP and CXR-RePaiR. CLIP, trained on a general-purpose dataset, struggles with medical image-report retrieval, highlighting the importance of domain-specific training data. The evaluation of this work suggests that more effort needs to be spent on improving the robustness of these models. By addressing these limitations, we can develop more reliable cross-domain retrieval models for medical applications.
Translating Natural Language Queries to SQL Using the T5 Model
Dec 12, 2023Abstract:This paper presents the development process of a natural language to SQL model using the T5 model as the basis. The models, developed in August 2022 for an online transaction processing system and a data warehouse, have a 73\% and 84\% exact match accuracy respectively. These models, in conjunction with other work completed in the research project, were implemented for several companies and used successfully on a daily basis. The approach used in the model development could be implemented in a similar fashion for other database environments and with a more powerful pre-trained language model.
An Adaptive Kernel Approach to Federated Learning of Heterogeneous Causal Effects
Jan 01, 2023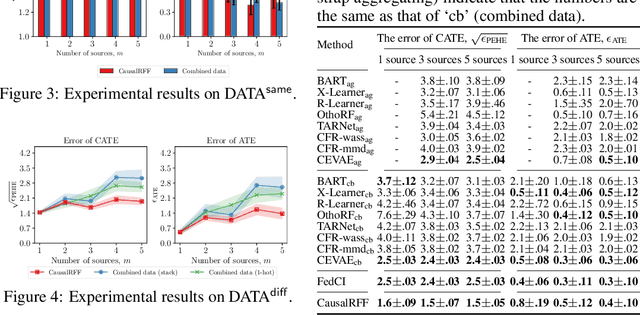
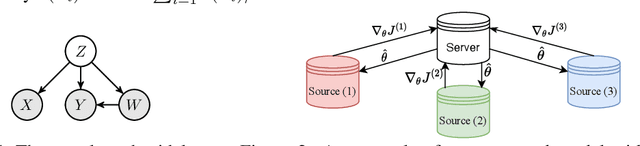
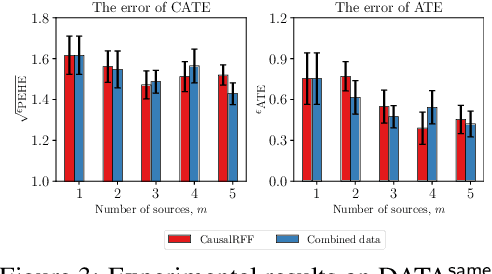
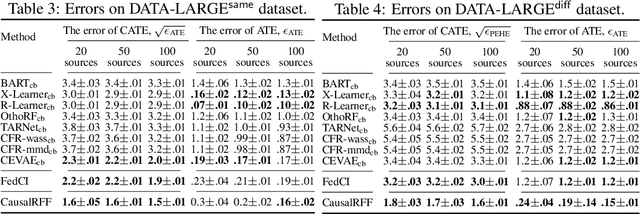
Abstract:We propose a new causal inference framework to learn causal effects from multiple, decentralized data sources in a federated setting. We introduce an adaptive transfer algorithm that learns the similarities among the data sources by utilizing Random Fourier Features to disentangle the loss function into multiple components, each of which is associated with a data source. The data sources may have different distributions; the causal effects are independently and systematically incorporated. The proposed method estimates the similarities among the sources through transfer coefficients, and hence requiring no prior information about the similarity measures. The heterogeneous causal effects can be estimated with no sharing of the raw training data among the sources, thus minimizing the risk of privacy leak. We also provide minimax lower bounds to assess the quality of the parameters learned from the disparate sources. The proposed method is empirically shown to outperform the baselines on decentralized data sources with dissimilar distributions.
Federated Estimation of Causal Effects from Observational Data
May 31, 2021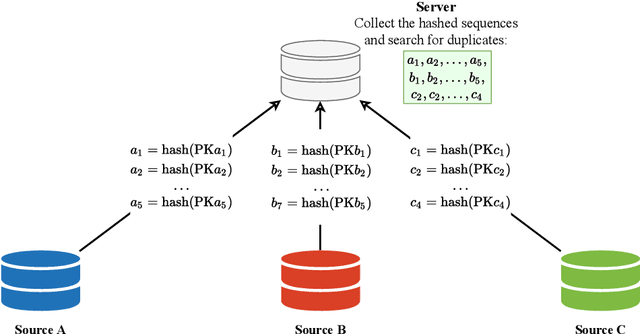
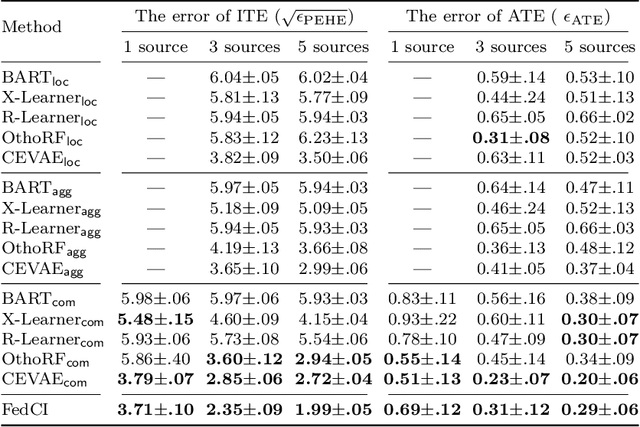
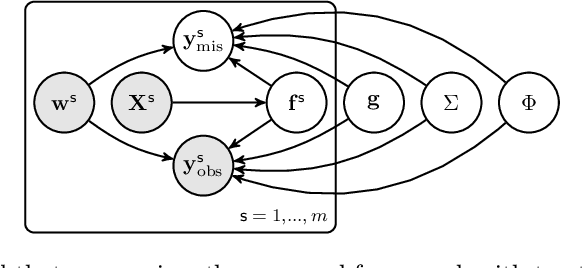
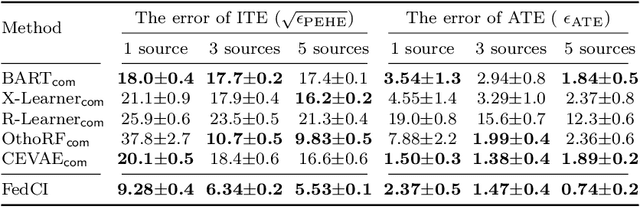
Abstract:Many modern applications collect data that comes in federated spirit, with data kept locally and undisclosed. Till date, most insight into the causal inference requires data to be stored in a central repository. We present a novel framework for causal inference with federated data sources. We assess and integrate local causal effects from different private data sources without centralizing them. Then, the treatment effects on subjects from observational data using a non-parametric reformulation of the classical potential outcomes framework is estimated. We model the potential outcomes as a random function distributed by Gaussian processes, whose defining parameters can be efficiently learned from multiple data sources, respecting privacy constraints. We demonstrate the promise and efficiency of the proposed approach through a set of simulated and real-world benchmark examples.
Generative Parameter Sampler For Scalable Uncertainty Quantification
Jun 02, 2019
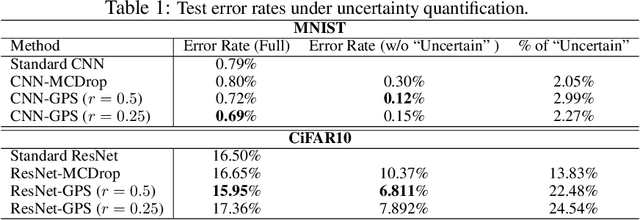
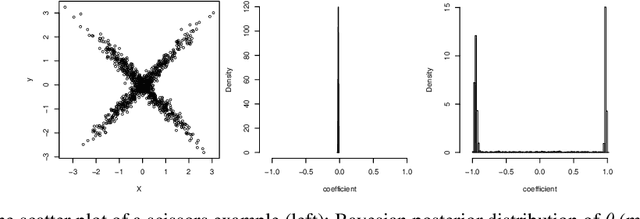
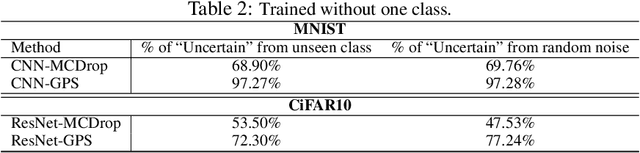
Abstract:Uncertainty quantification has been a core of the statistical machine learning, but its computational bottleneck has been a serious challenge for both Bayesians and frequentists. We propose a model-based framework in quantifying uncertainty, called predictive-matching Generative Parameter Sampler (GPS). This procedure considers an Uncertainty Quantification (UQ) distribution on the targeted parameter, which matches the corresponding predictive distribution to the observed data. This framework adopts a hierarchical modeling perspective such that each observation is modeled by an individual parameter. This individual parameterization permits the resulting inference to be computationally scalable and robust to outliers. Our approach is illustrated for linear models, Poisson processes, and deep neural networks for classification. The results show that the GPS is successful in providing uncertainty quantification as well as additional flexibility beyond what is allowed by classical statistical procedures under the postulated statistical models.
Simulation and Calibration of a Fully Bayesian Marked Multidimensional Hawkes Process with Dissimilar Decays
Mar 13, 2018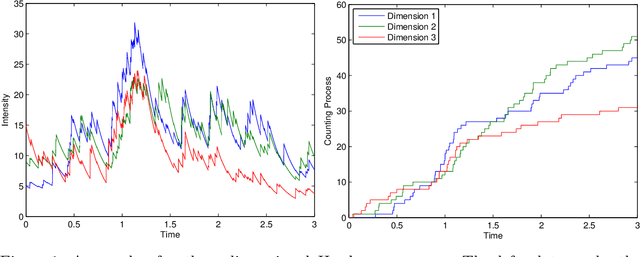
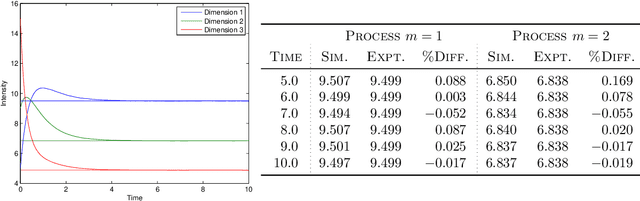
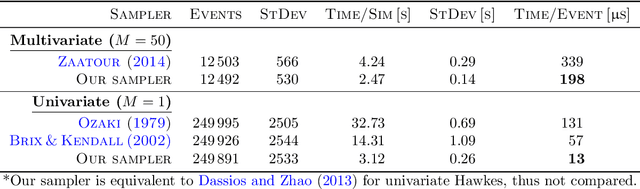
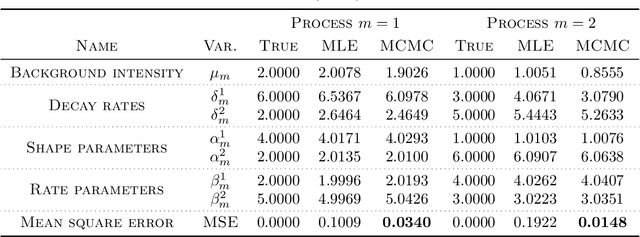
Abstract:We propose a simulation method for multidimensional Hawkes processes based on superposition theory of point processes. This formulation allows us to design efficient simulations for Hawkes processes with differing exponentially decaying intensities. We demonstrate that inter-arrival times can be decomposed into simpler auxiliary variables that can be sampled directly, giving exact simulation with no approximation. We establish that the auxiliary variables provides information on the parent process for each event time. The algorithm correctness is shown by verifying the simulated intensities with their theoretical moments. A modular inference procedure consisting of Gibbs samplers through the auxiliary variable augmentation and adaptive rejection sampling is presented. Finally, we compare our proposed simulation method against existing methods, and find significant improvement in terms of algorithm speed. Our inference algorithm is used to discover the strengths of mutually excitations in real dark networks.
* 24 pages, long version of ACML paper with supplementary material
Variational Inference for Gaussian Process with Panel Count Data
Mar 12, 2018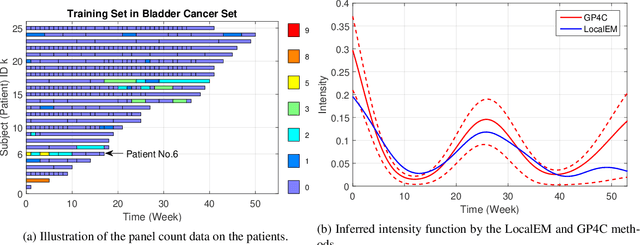
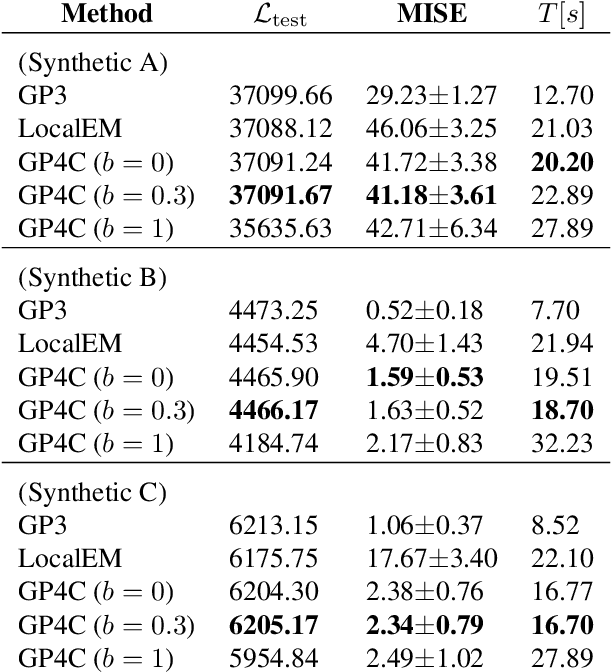
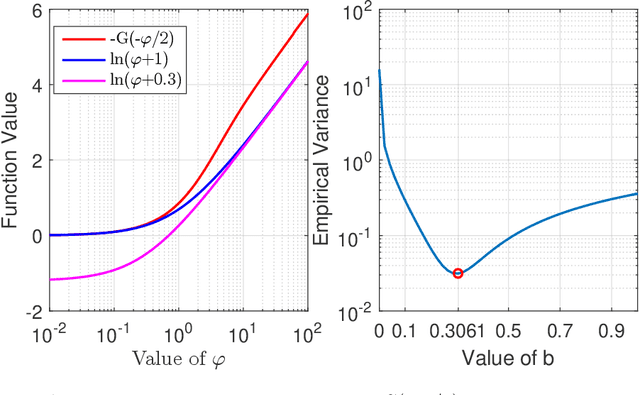
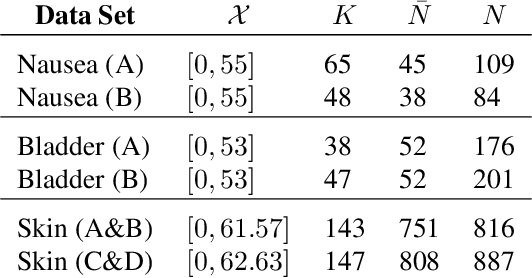
Abstract:We present the first framework for Gaussian-process-modulated Poisson processes when the temporal data appear in the form of panel counts. Panel count data frequently arise when experimental subjects are observed only at discrete time points and only the numbers of occurrences of the events between subsequent observation times are available. The exact occurrence timestamps of the events are unknown. The method of conducting the efficient variational inference is presented, based on the assumption of a Gaussian-process-modulated intensity function. We derive a tractable lower bound to alleviate the problems of the intractable evidence lower bound inherent in the variational inference framework. Our algorithm outperforms classical methods on both synthetic and three real panel count sets.
A Tutorial on Hawkes Processes for Events in Social Media
Oct 09, 2017
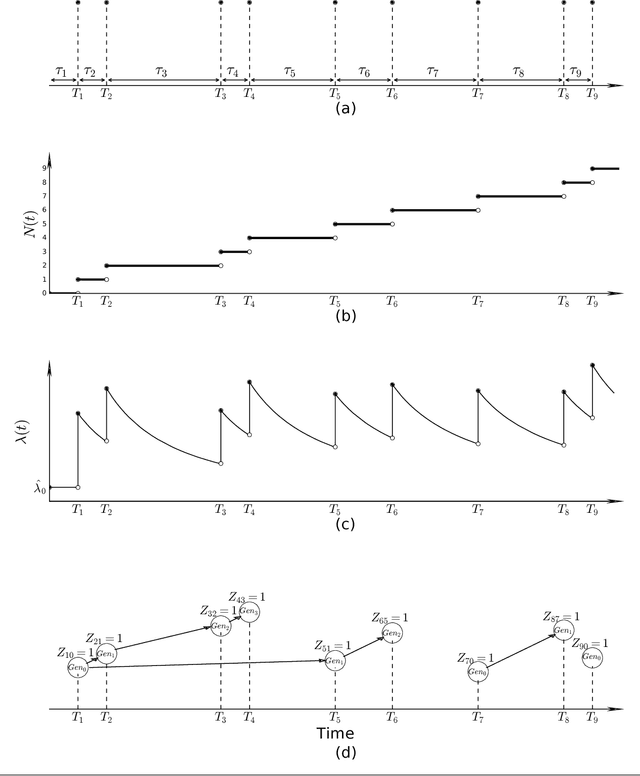
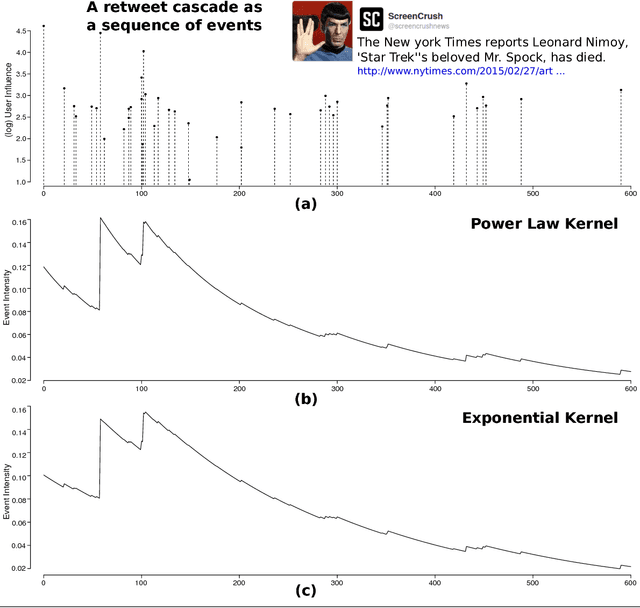
Abstract:This chapter provides an accessible introduction for point processes, and especially Hawkes processes, for modeling discrete, inter-dependent events over continuous time. We start by reviewing the definitions and the key concepts in point processes. We then introduce the Hawkes process, its event intensity function, as well as schemes for event simulation and parameter estimation. We also describe a practical example drawn from social media data - we show how to model retweet cascades using a Hawkes self-exciting process. We presents a design of the memory kernel, and results on estimating parameters and predicting popularity. The code and sample event data are available as an online appendix
Hawkes Processes with Stochastic Excitations
Sep 22, 2016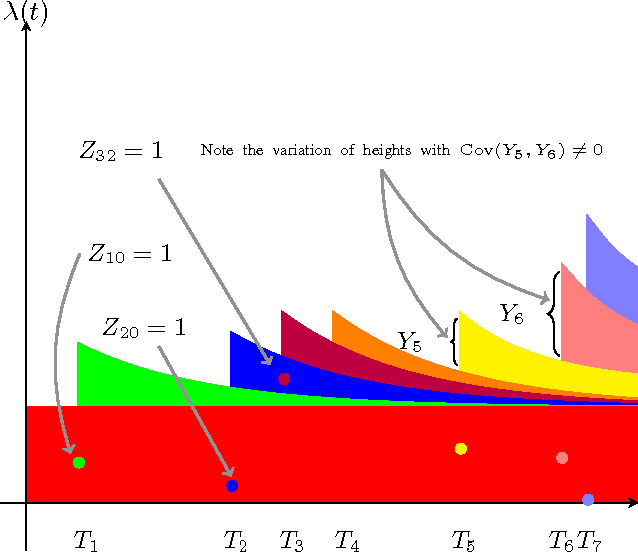
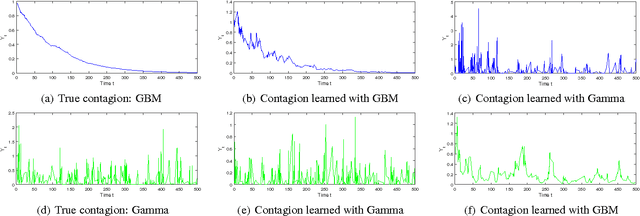
Abstract:We propose an extension to Hawkes processes by treating the levels of self-excitation as a stochastic differential equation. Our new point process allows better approximation in application domains where events and intensities accelerate each other with correlated levels of contagion. We generalize a recent algorithm for simulating draws from Hawkes processes whose levels of excitation are stochastic processes, and propose a hybrid Markov chain Monte Carlo approach for model fitting. Our sampling procedure scales linearly with the number of required events and does not require stationarity of the point process. A modular inference procedure consisting of a combination between Gibbs and Metropolis Hastings steps is put forward. We recover expectation maximization as a special case. Our general approach is illustrated for contagion following geometric Brownian motion and exponential Langevin dynamics.
* Copy of ICML paper
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge