Minsuk Shin
Neural Bootstrapper
Oct 02, 2020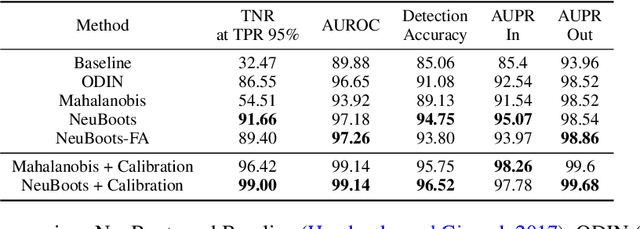
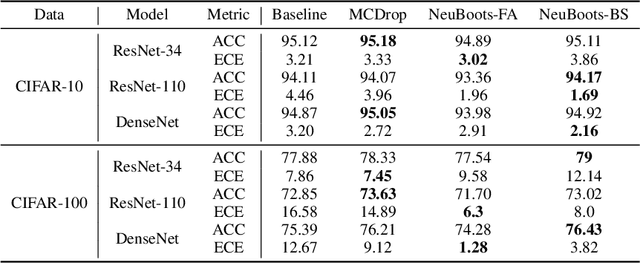

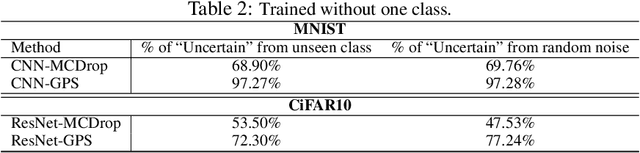
Abstract:Bootstrapping has been a primary tool for uncertainty quantification, and their theoretical and computational properties have been investigated in the field of statistics and machine learning. However, due to its nature of repetitive computations, the computational burden required to implement bootstrap procedures for the neural network is painfully heavy, and this fact seriously hurdles the practical use of these procedures on the uncertainty estimation of modern deep learning. To overcome the inconvenience, we propose a procedure called \emph{Neural Bootstrapper} (NeuBoots). We reveal that the NeuBoots stably generate valid bootstrap samples that coincide with the desired target samples with minimal extra computational cost compared to traditional bootstrapping. Consequently, NeuBoots makes it feasible to construct bootstrap confidence intervals of outputs of neural networks and quantify their predictive uncertainty. We also suggest NeuBoots for deep convolutional neural networks to consider its utility in image classification tasks, including calibration, detection of out-of-distribution samples, and active learning. Empirical results demonstrate that NeuBoots is significantly beneficial for the above purposes.
Generative Parameter Sampler For Scalable Uncertainty Quantification
Jun 02, 2019
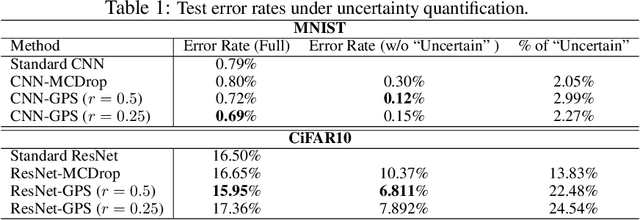
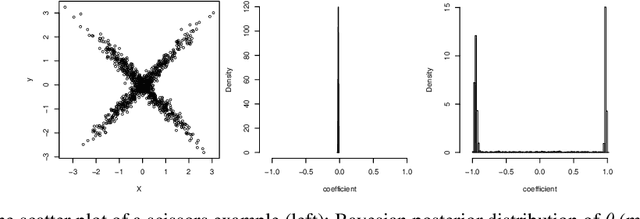
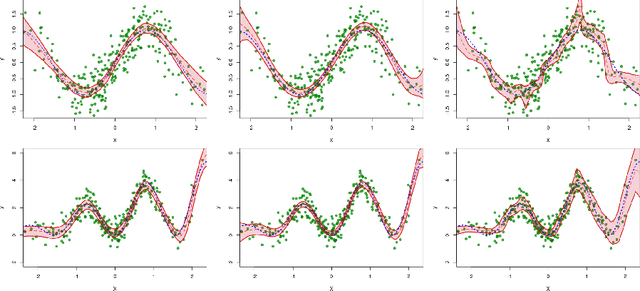
Abstract:Uncertainty quantification has been a core of the statistical machine learning, but its computational bottleneck has been a serious challenge for both Bayesians and frequentists. We propose a model-based framework in quantifying uncertainty, called predictive-matching Generative Parameter Sampler (GPS). This procedure considers an Uncertainty Quantification (UQ) distribution on the targeted parameter, which matches the corresponding predictive distribution to the observed data. This framework adopts a hierarchical modeling perspective such that each observation is modeled by an individual parameter. This individual parameterization permits the resulting inference to be computationally scalable and robust to outliers. Our approach is illustrated for linear models, Poisson processes, and deep neural networks for classification. The results show that the GPS is successful in providing uncertainty quantification as well as additional flexibility beyond what is allowed by classical statistical procedures under the postulated statistical models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge