TurboBoA: Faster and Exact Attention-aware Quantization without Backpropagation

The rapid growth of large language models (LLMs) has heightened the importance of post-training quantization (PTQ) for reducing memory and computation costs. Among PTQ methods, GPTQ has gained significant attention for its efficiency, enabling billion-scale LLMs to be quantized within a few GPU hours. However, GPTQ's assumption of layer-wise independence leads to severe accuracy drops in low-bit regimes. Recently, BoA improved upon GPTQ by incorporating inter-layer dependencies within attention modules, but its reliance on sequential quantization across all out-channels makes it substantially less efficient. In this paper, we propose TurboBoA, a new backpropagation-free PTQ algorithm that preserves the accuracy benefits of BoA while significantly accelerating the process. The proposed TurboBoA introduces three key innovations: (i) joint quantization of multiple out-channels with a closed-form error compensation rule, which reduces sequential bottlenecks and yields more than a three-fold speedup; (ii) a correction mechanism for errors propagated from preceding quantized layers; and (iii) adaptive grid computation with coordinate descent refinement to maintain alignment during iterative updates. Extensive experiments demonstrate that TurboBoA delivers substantial acceleration over BoA while consistently improving accuracy. When combined with outlier suppression techniques, it achieves state-of-the-art results in both weight-only and weight-activation quantization. The code will be available at https://github.com/SamsungLabs/TurboBoA.

Two-Stage Grid Optimization for Group-wise Quantization of LLMs

Group-wise quantization is an effective strategy for mitigating accuracy degradation in low-bit quantization of large language models (LLMs). Among existing methods, GPTQ has been widely adopted due to its efficiency; however, it neglects input statistics and inter-group correlations when determining group scales, leading to a mismatch with its goal of minimizing layer-wise reconstruction loss. In this work, we propose a two-stage optimization framework for group scales that explicitly minimizes the layer-wise reconstruction loss. In the first stage, performed prior to GPTQ, we initialize each group scale to minimize the group-wise reconstruction loss, thereby incorporating input statistics. In the second stage, we freeze the integer weights obtained via GPTQ and refine the group scales to minimize the layer-wise reconstruction loss. To this end, we employ the coordinate descent algorithm and derive a closed-form update rule, which enables efficient refinement without costly numerical optimization. Notably, our derivation incorporates the quantization errors from preceding layers to prevent error accumulation. Experimental results demonstrate that our method consistently enhances group-wise quantization, achieving higher accuracy with negligible overhead.

Attention-aware Post-training Quantization without Backpropagation

Quantization is a promising solution for deploying large-scale language models (LLMs) on resource-constrained devices. Existing quantization approaches, however, rely on gradient-based optimization, regardless of it being post-training quantization (PTQ) or quantization-aware training (QAT), which becomes problematic for hyper-scale LLMs with billions of parameters. This overhead can be alleviated via recently proposed backpropagation-free PTQ methods; however, their performance is somewhat limited by their lack of consideration of inter-layer dependencies. In this paper, we thus propose a novel PTQ algorithm that considers inter-layer dependencies without relying on backpropagation. The fundamental concept involved is the development of attention-aware Hessian matrices, which facilitates the consideration of inter-layer dependencies within the attention module. Extensive experiments demonstrate that the proposed algorithm significantly outperforms conventional PTQ methods, particularly for low bit-widths.

Towards Next-Level Post-Training Quantization of Hyper-Scale Transformers

With the increasing complexity of generative AI models, post-training quantization (PTQ) has emerged as a promising solution for deploying hyper-scale models on edge devices such as mobile devices and TVs. Existing PTQ schemes, however, consume considerable time and resources, which could be a bottleneck in real situations where frequent model updates and multiple hyper-parameter tunings are required. As a cost-effective alternative, one-shot PTQ schemes have been proposed. Still, the performance is somewhat limited because they cannot consider the inter-layer dependency within the attention module, which is a very important feature of Transformers. In this paper, we thus propose a novel PTQ algorithm that balances accuracy and efficiency. The key idea of the proposed algorithm called aespa is to perform quantization layer-wise for efficiency while considering cross-layer dependency to preserve the attention score. Through extensive experiments on various language models and complexity analysis, we demonstrate that aespa is accurate and efficient in quantizing Transformer models.

Genie: Show Me the Data for Quantization

Zero-shot quantization is a promising approach for developing lightweight deep neural networks when data is inaccessible owing to various reasons, including cost and issues related to privacy. By utilizing the learned parameters (statistics) of FP32-pre-trained models, zero-shot quantization schemes focus on generating synthetic data by minimizing the distance between the learned parameters ($\mu$ and $\sigma$) and distributions of intermediate activations. Subsequently, they distill knowledge from the pre-trained model (\textit{teacher}) to the quantized model (\textit{student}) such that the quantized model can be optimized with the synthetic dataset. In general, zero-shot quantization comprises two major elements: synthesizing datasets and quantizing models. However, thus far, zero-shot quantization has primarily been discussed in the context of quantization-aware training methods, which require task-specific losses and long-term optimization as much as retraining. We thus introduce a post-training quantization scheme for zero-shot quantization that produces high-quality quantized networks within a few hours on even half an hour. Furthermore, we propose a framework called \genie~that generates data suited for post-training quantization. With the data synthesized by \genie, we can produce high-quality quantized models without real datasets, which is comparable to few-shot quantization. We also propose a post-training quantization algorithm to enhance the performance of quantized models. By combining them, we can bridge the gap between zero-shot and few-shot quantization while significantly improving the quantization performance compared to that of existing approaches. In other words, we can obtain a unique state-of-the-art zero-shot quantization approach.

Modulating Regularization Frequency for Efficient Compression-Aware Model Training

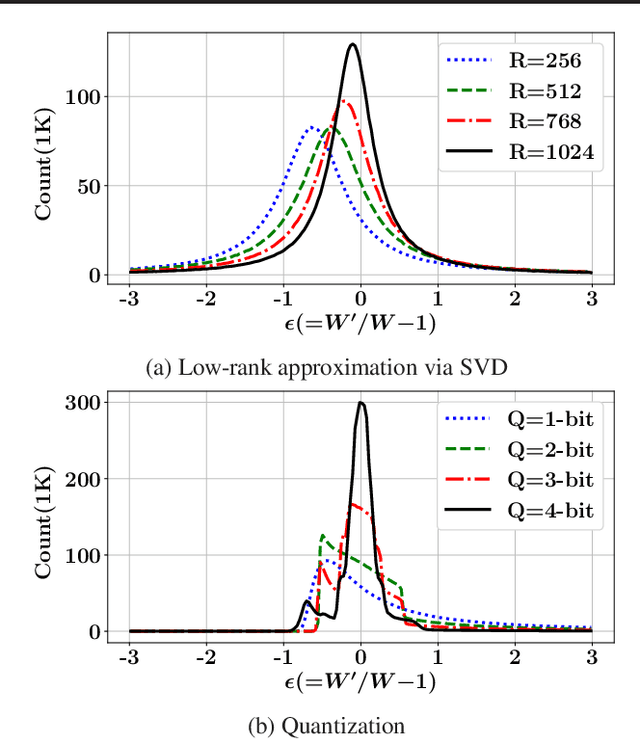
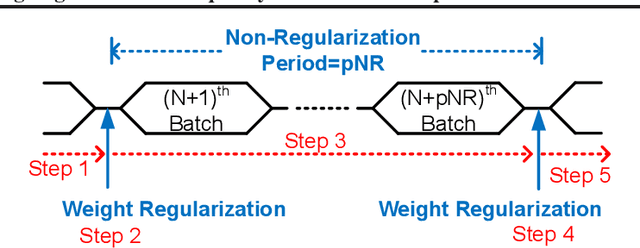
While model compression is increasingly important because of large neural network size, compression-aware training is challenging as it needs sophisticated model modifications and longer training time.In this paper, we introduce regularization frequency (i.e., how often compression is performed during training) as a new regularization technique for a practical and efficient compression-aware training method. For various regularization techniques, such as weight decay and dropout, optimizing the regularization strength is crucial to improve generalization in Deep Neural Networks (DNNs). While model compression also demands the right amount of regularization, the regularization strength incurred by model compression has been controlled only by compression ratio. Throughout various experiments, we show that regularization frequency critically affects the regularization strength of model compression. Combining regularization frequency and compression ratio, the amount of weight updates by model compression per mini-batch can be optimized to achieve the best model accuracy. Modulating regularization frequency is implemented by occasional model compression while conventional compression-aware training is usually performed for every mini-batch.

Sequential Encryption of Sparse Neural Networks Toward Optimum Representation of Irregular Sparsity

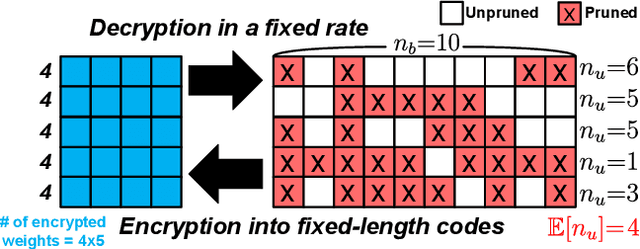
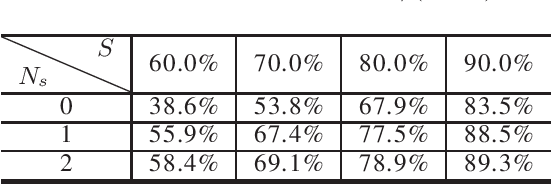
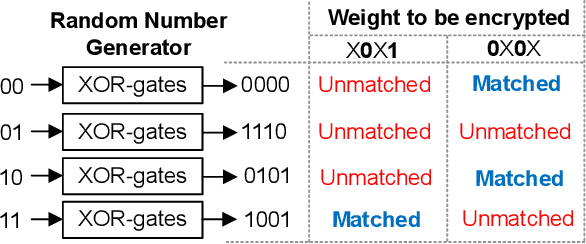
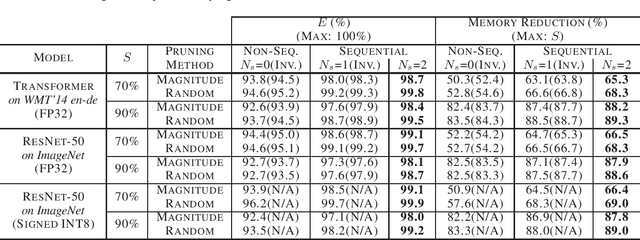
Even though fine-grained pruning techniques achieve a high compression ratio, conventional sparsity representations (such as CSR) associated with irregular sparsity degrade parallelism significantly. Practical pruning methods, thus, usually lower pruning rates (by structured pruning) to improve parallelism. In this paper, we study fixed-to-fixed (lossless) encryption architecture/algorithm to support fine-grained pruning methods such that sparse neural networks can be stored in a highly regular structure. We first estimate the maximum compression ratio of encryption-based compression using entropy. Then, as an effort to push the compression ratio to the theoretical maximum (by entropy), we propose a sequential fixed-to-fixed encryption scheme. We demonstrate that our proposed compression scheme achieves almost the maximum compression ratio for the Transformer and ResNet-50 pruned by various fine-grained pruning methods.

Q-Rater: Non-Convex Optimization for Post-Training Uniform Quantization

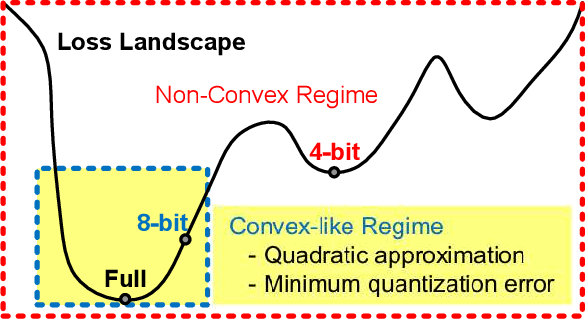
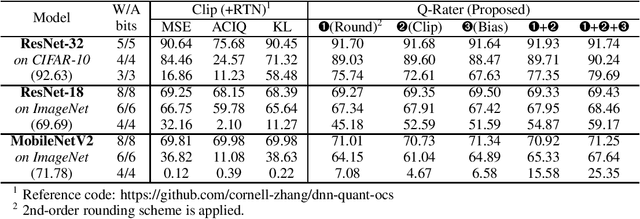
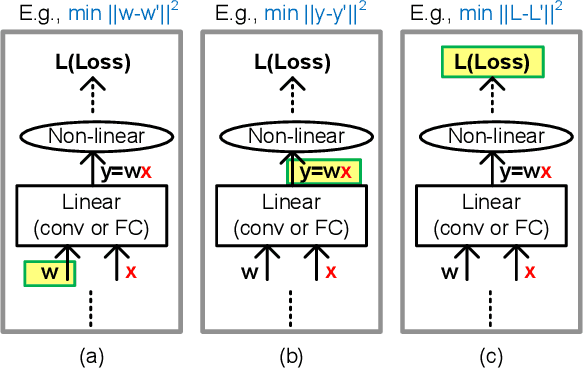
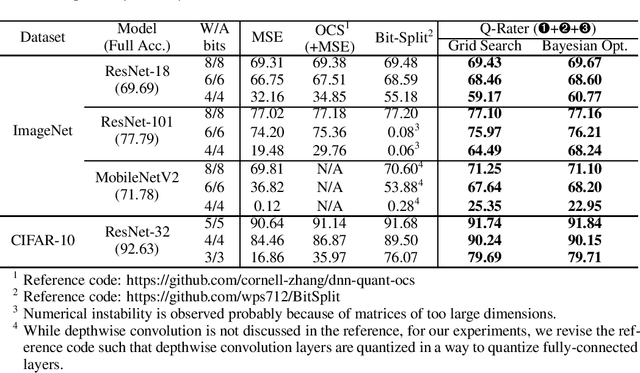
Various post-training uniform quantization methods have usually been studied based on convex optimization. As a result, most previous ones rely on the quantization error minimization and/or quadratic approximations. Such approaches are computationally efficient and reasonable when a large number of quantization bits are employed. When the number of quantization bits is relatively low, however, non-convex optimization is unavoidable to improve model accuracy. In this paper, we propose a new post-training uniform quantization technique considering non-convexity. We empirically show that hyper-parameters for clipping and rounding of weights and activations can be explored by monitoring task loss. Then, an optimally searched set of hyper-parameters is frozen to proceed to the next layer such that an incremental non-convex optimization is enabled for post-training quantization. Throughout extensive experimental results using various models, our proposed technique presents higher model accuracy, especially for a low-bit quantization.

Extremely Low Bit Transformer Quantization for On-Device Neural Machine Translation

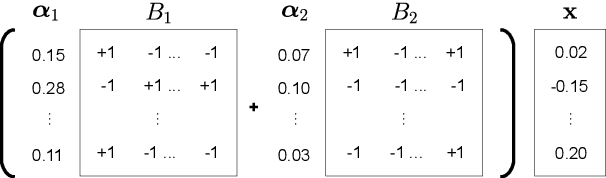
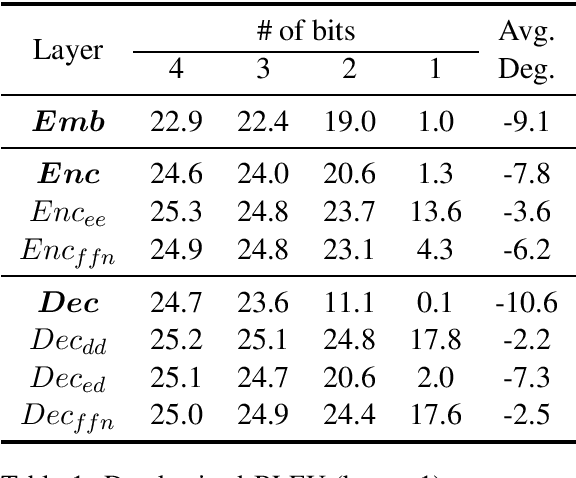
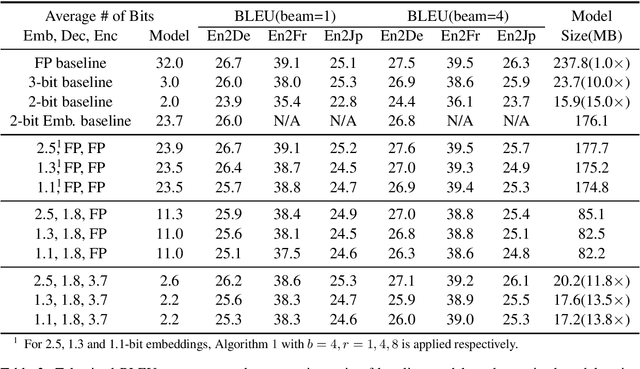
The deployment of widely used Transformer architecture is challenging because of heavy computation load and memory overhead during inference, especially when the target device is limited in computational resources such as mobile or edge devices. Quantization is an effective technique to address such challenges. Our analysis shows that for a given number of quantization bits, each block of Transformer contributes to translation quality and inference computations in different manners. Moreover, even inside an embedding block, each word presents vastly different contributions. Correspondingly, we propose a mixed precision quantization strategy to represent Transformer weights by an extremely low number of bits (e.g., under 3 bits). For example, for each word in an embedding block, we assign different quantization bits based on statistical property. Our quantized Transformer model achieves 11.8$\times$ smaller model size than the baseline model, with less than -0.5 BLEU. We achieve 8.3$\times$ reduction in run-time memory footprints and 3.5$\times$ speed up (Galaxy N10+) such that our proposed compression strategy enables efficient implementation for on-device NMT.

FleXOR: Trainable Fractional Quantization

Quantization based on the binary codes is gaining attention because each quantized bit can be directly utilized for computations without dequantization using look-up tables. Previous attempts, however, only allow for integer numbers of quantization bits, which ends up restricting the search space for compression ratio and accuracy. In this paper, we propose an encryption algorithm/architecture to compress quantized weights so as to achieve fractional numbers of bits per weight.Decryption during inference is implemented by digital XOR-gate networks added into the neural network model while XOR gates are described by utilizing tanh(x) for backward propagation to enable gradient calculations. We perform experiments using MNIST, CIFAR-10, and ImageNet to show that inserting XOR gates learns quantization/encrypted bit decisions through training and obtains high accuracy even for fractional sub 1-bit weights. As a result, our proposed method yields smaller size and higher model accuracy compared to binary neural networks.