Sequential Encryption of Sparse Neural Networks Toward Optimum Representation of Irregular Sparsity

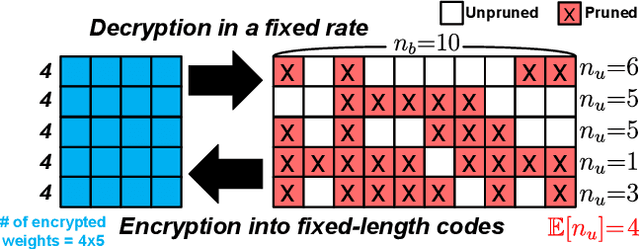
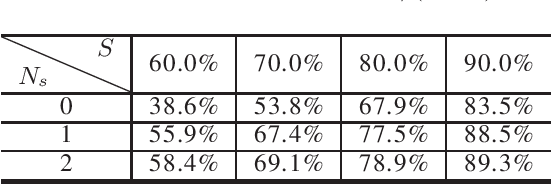
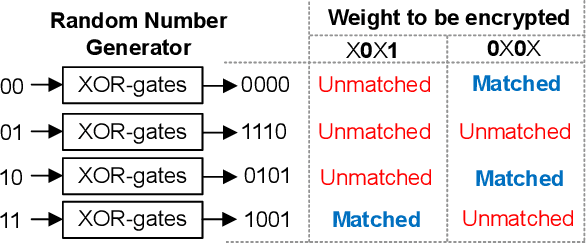
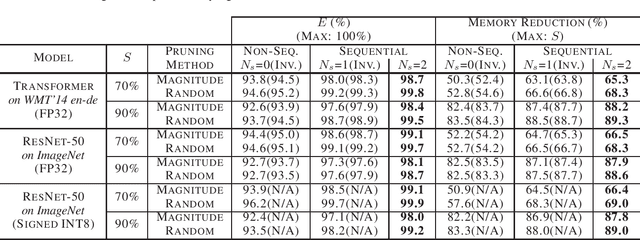
Even though fine-grained pruning techniques achieve a high compression ratio, conventional sparsity representations (such as CSR) associated with irregular sparsity degrade parallelism significantly. Practical pruning methods, thus, usually lower pruning rates (by structured pruning) to improve parallelism. In this paper, we study fixed-to-fixed (lossless) encryption architecture/algorithm to support fine-grained pruning methods such that sparse neural networks can be stored in a highly regular structure. We first estimate the maximum compression ratio of encryption-based compression using entropy. Then, as an effort to push the compression ratio to the theoretical maximum (by entropy), we propose a sequential fixed-to-fixed encryption scheme. We demonstrate that our proposed compression scheme achieves almost the maximum compression ratio for the Transformer and ResNet-50 pruned by various fine-grained pruning methods.

Q-Rater: Non-Convex Optimization for Post-Training Uniform Quantization

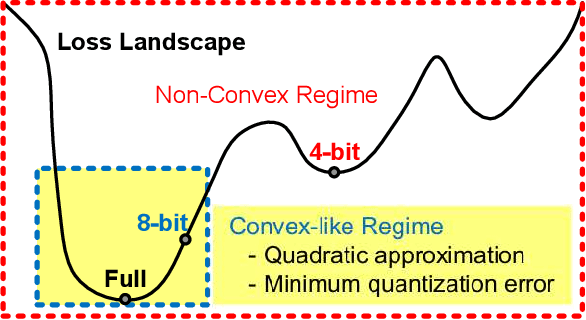
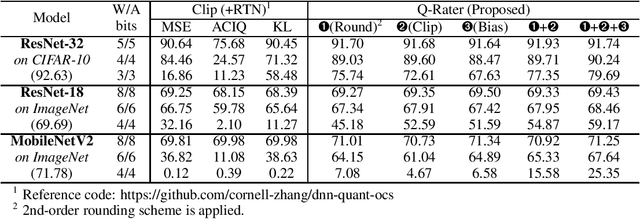
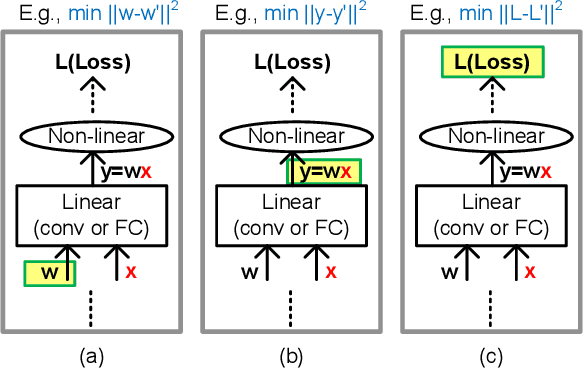
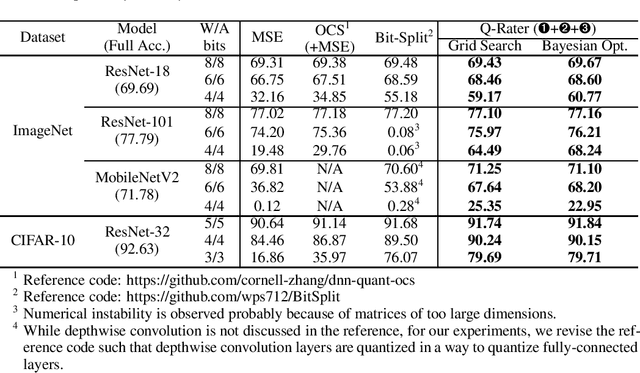
Various post-training uniform quantization methods have usually been studied based on convex optimization. As a result, most previous ones rely on the quantization error minimization and/or quadratic approximations. Such approaches are computationally efficient and reasonable when a large number of quantization bits are employed. When the number of quantization bits is relatively low, however, non-convex optimization is unavoidable to improve model accuracy. In this paper, we propose a new post-training uniform quantization technique considering non-convexity. We empirically show that hyper-parameters for clipping and rounding of weights and activations can be explored by monitoring task loss. Then, an optimally searched set of hyper-parameters is frozen to proceed to the next layer such that an incremental non-convex optimization is enabled for post-training quantization. Throughout extensive experimental results using various models, our proposed technique presents higher model accuracy, especially for a low-bit quantization.