Q-Rater: Non-Convex Optimization for Post-Training Uniform Quantization
Paper and Code
May 05, 2021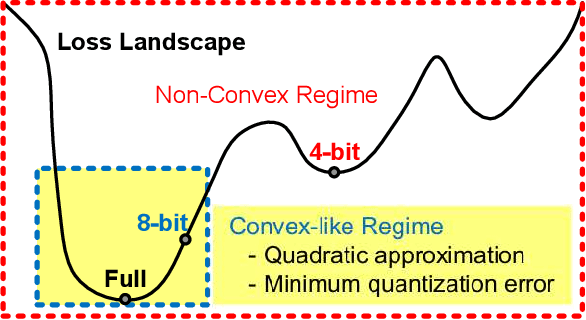
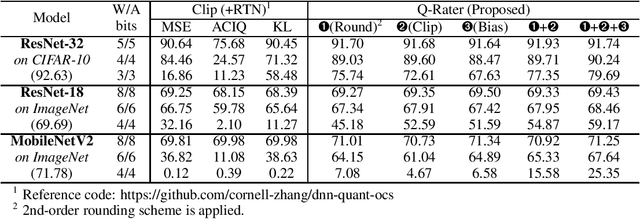
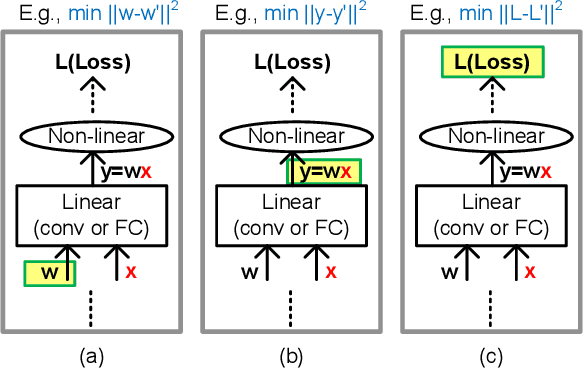
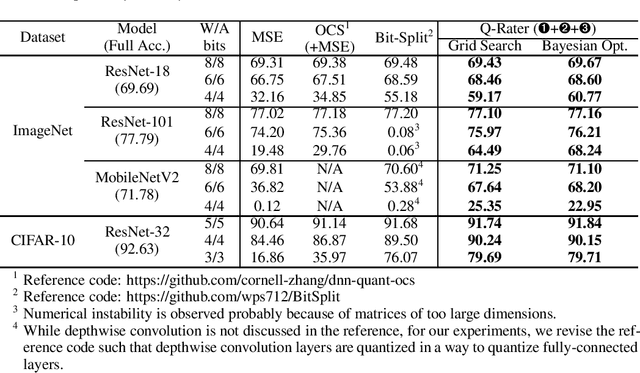
Various post-training uniform quantization methods have usually been studied based on convex optimization. As a result, most previous ones rely on the quantization error minimization and/or quadratic approximations. Such approaches are computationally efficient and reasonable when a large number of quantization bits are employed. When the number of quantization bits is relatively low, however, non-convex optimization is unavoidable to improve model accuracy. In this paper, we propose a new post-training uniform quantization technique considering non-convexity. We empirically show that hyper-parameters for clipping and rounding of weights and activations can be explored by monitoring task loss. Then, an optimally searched set of hyper-parameters is frozen to proceed to the next layer such that an incremental non-convex optimization is enabled for post-training quantization. Throughout extensive experimental results using various models, our proposed technique presents higher model accuracy, especially for a low-bit quantization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge