Bandit Learning to Rank with Position-Based Click Models: Personalized and Equal Treatments

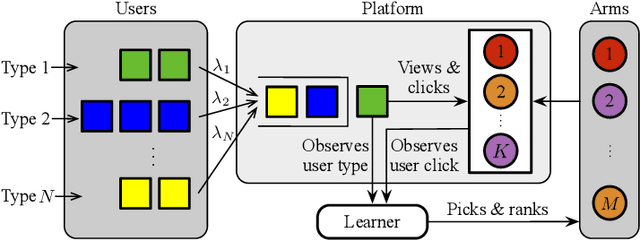
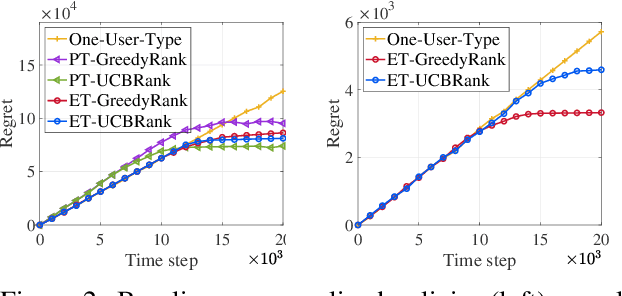
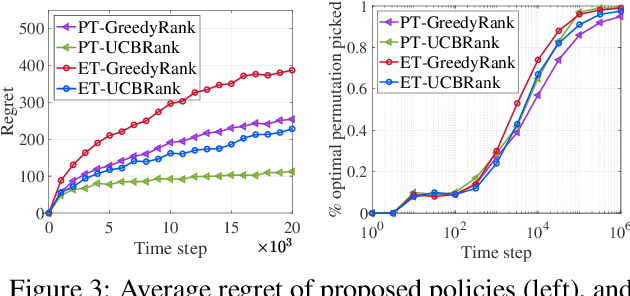
Online learning to rank (ONL2R) is a foundational problem for recommender systems and has received increasing attention in recent years. Among the existing approaches for ONL2R, a natural modeling architecture is the multi-armed bandit framework coupled with the position-based click model. However, developing efficient online learning policies for MAB-based ONL2R with position-based click models is highly challenging due to the combinatorial nature of the problem, and partial observability in the position-based click model. To date, results in MAB-based ONL2R with position-based click models remain rather limited, which motivates us to fill this gap in this work. Our main contributions in this work are threefold: i) We propose the first general MAB framework that captures all key ingredients of ONL2R with position-based click models. Our model considers personalized and equal treatments in ONL2R ranking recommendations, both of which are widely used in practice; ii) Based on the above analytical framework, we develop two unified greed- and UCB-based policies called GreedyRank and UCBRank, each of which can be applied to personalized and equal ranking treatments; and iii) We show that both GreedyRank and UCBRank enjoy $O(\sqrt{t}\ln t)$ and $O(\sqrt{t\ln t})$ anytime sublinear regret for personalized and equal treatment, respectively. For the fundamentally hard equal ranking treatment, we identify classes of collective utility functions and their associated sufficient conditions under which $O(\sqrt{t}\ln t)$ and $O(\sqrt{t\ln t})$ anytime sublinear regrets are still achievable for GreedyRank and UCBRank, respectively. Our numerical experiments also verify our theoretical results and demonstrate the efficiency of GreedyRank and UCBRank in seeking the optimal action under various problem settings.

Multi-Label Learning to Rank through Multi-Objective Optimization

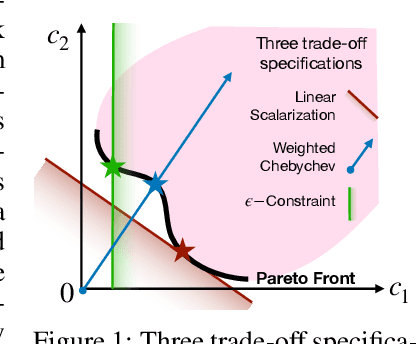
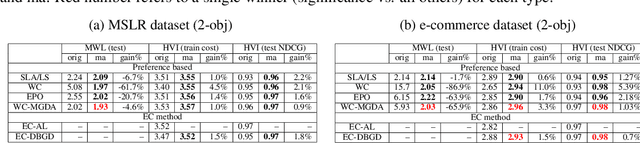
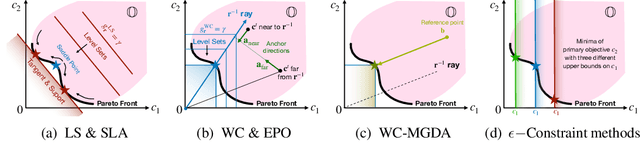
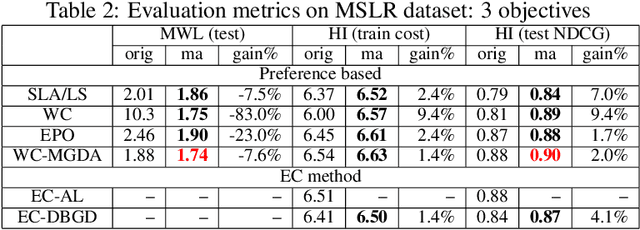
Learning to Rank (LTR) technique is ubiquitous in the Information Retrieval system nowadays, especially in the Search Ranking application. The query-item relevance labels typically used to train the ranking model are often noisy measurements of human behavior, e.g., product rating for product search. The coarse measurements make the ground truth ranking non-unique with respect to a single relevance criterion. To resolve ambiguity, it is desirable to train a model using many relevance criteria, giving rise to Multi-Label LTR (MLLTR). Moreover, it formulates multiple goals that may be conflicting yet important to optimize for simultaneously, e.g., in product search, a ranking model can be trained based on product quality and purchase likelihood to increase revenue. In this research, we leverage the Multi-Objective Optimization (MOO) aspect of the MLLTR problem and employ recently developed MOO algorithms to solve it. Specifically, we propose a general framework where the information from labels can be combined in a variety of ways to meaningfully characterize the trade-off among the goals. Our framework allows for any gradient based MOO algorithm to be used for solving the MLLTR problem. We test the proposed framework on two publicly available LTR datasets and one e-commerce dataset to show its efficacy.

A Parallel Algorithm for Exact Bayesian Structure Discovery in Bayesian Networks

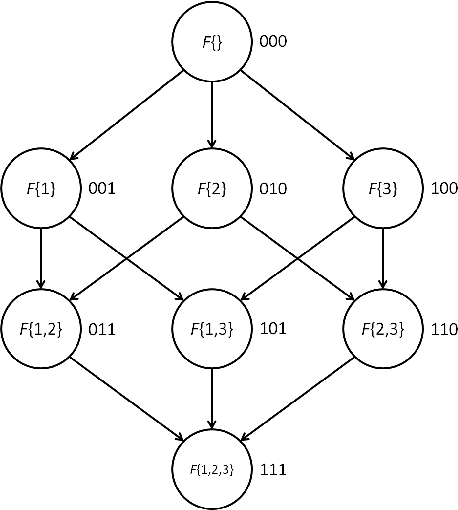
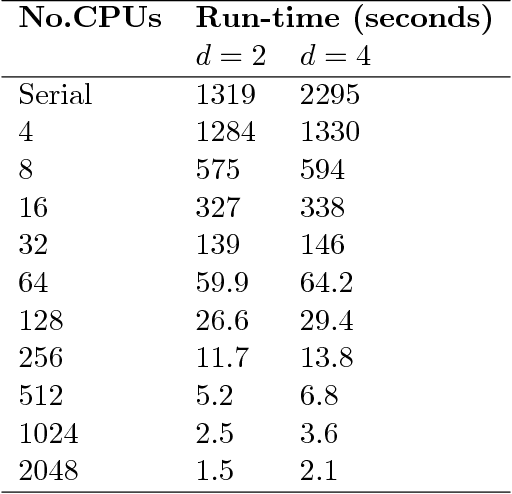
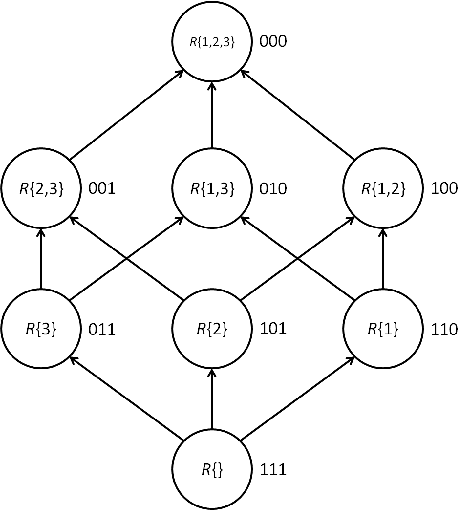
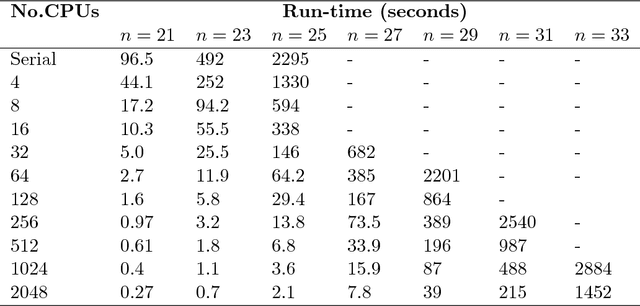
Exact Bayesian structure discovery in Bayesian networks requires exponential time and space. Using dynamic programming (DP), the fastest known sequential algorithm computes the exact posterior probabilities of structural features in $O(2(d+1)n2^n)$ time and space, if the number of nodes (variables) in the Bayesian network is $n$ and the in-degree (the number of parents) per node is bounded by a constant $d$. Here we present a parallel algorithm capable of computing the exact posterior probabilities for all $n(n-1)$ edges with optimal parallel space efficiency and nearly optimal parallel time efficiency. That is, if $p=2^k$ processors are used, the run-time reduces to $O(5(d+1)n2^{n-k}+k(n-k)^d)$ and the space usage becomes $O(n2^{n-k})$ per processor. Our algorithm is based the observation that the subproblems in the sequential DP algorithm constitute a $n$-$D$ hypercube. We take a delicate way to coordinate the computation of correlated DP procedures such that large amount of data exchange is suppressed. Further, we develop parallel techniques for two variants of the well-known \emph{zeta transform}, which have applications outside the context of Bayesian networks. We demonstrate the capability of our algorithm on datasets with up to 33 variables and its scalability on up to 2048 processors. We apply our algorithm to a biological data set for discovering the yeast pheromone response pathways.