Olga Nikolova
A Parallel Algorithm for Exact Bayesian Structure Discovery in Bayesian Networks
Aug 13, 2016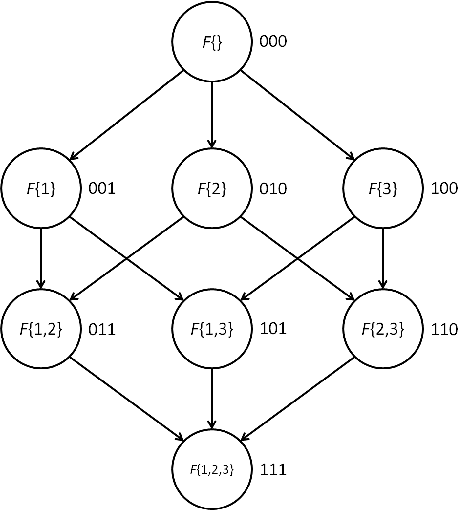
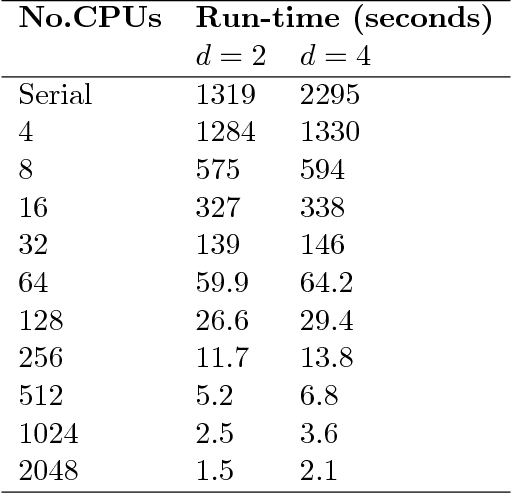
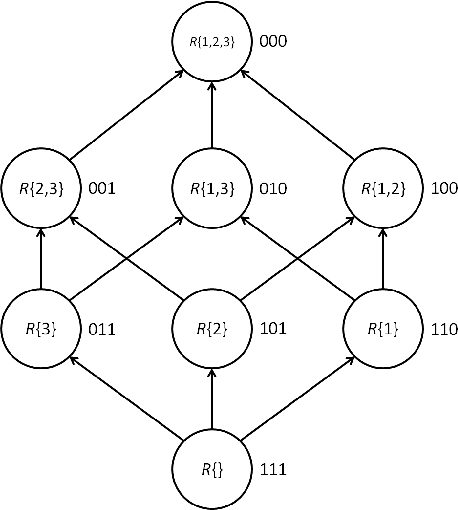
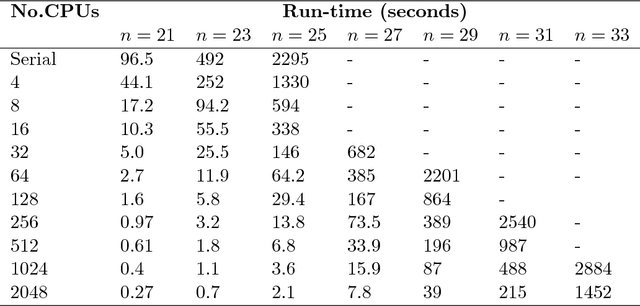
Abstract:Exact Bayesian structure discovery in Bayesian networks requires exponential time and space. Using dynamic programming (DP), the fastest known sequential algorithm computes the exact posterior probabilities of structural features in $O(2(d+1)n2^n)$ time and space, if the number of nodes (variables) in the Bayesian network is $n$ and the in-degree (the number of parents) per node is bounded by a constant $d$. Here we present a parallel algorithm capable of computing the exact posterior probabilities for all $n(n-1)$ edges with optimal parallel space efficiency and nearly optimal parallel time efficiency. That is, if $p=2^k$ processors are used, the run-time reduces to $O(5(d+1)n2^{n-k}+k(n-k)^d)$ and the space usage becomes $O(n2^{n-k})$ per processor. Our algorithm is based the observation that the subproblems in the sequential DP algorithm constitute a $n$-$D$ hypercube. We take a delicate way to coordinate the computation of correlated DP procedures such that large amount of data exchange is suppressed. Further, we develop parallel techniques for two variants of the well-known \emph{zeta transform}, which have applications outside the context of Bayesian networks. We demonstrate the capability of our algorithm on datasets with up to 33 variables and its scalability on up to 2048 processors. We apply our algorithm to a biological data set for discovering the yeast pheromone response pathways.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge