Cooperative neural networks (CoNN): Exploiting prior independence structure for improved classification

We propose a new approach, called cooperative neural networks (CoNN), which uses a set of cooperatively trained neural networks to capture latent representations that exploit prior given independence structure. The model is more flexible than traditional graphical models based on exponential family distributions, but incorporates more domain specific prior structure than traditional deep networks or variational autoencoders. The framework is very general and can be used to exploit the independence structure of any graphical model. We illustrate the technique by showing that we can transfer the independence structure of the popular Latent Dirichlet Allocation (LDA) model to a cooperative neural network, CoNN-sLDA. Empirical evaluation of CoNN-sLDA on supervised text classification tasks demonstrates that the theoretical advantages of prior independence structure can be realized in practice -we demonstrate a 23\% reduction in error on the challenging MultiSent data set compared to state-of-the-art.

Parallelized Kendall's Tau Coefficient Computation via SIMD Vectorized Sorting On Many-Integrated-Core Processors

Pairwise association measure is an important operation in data analytics. Kendall's tau coefficient is one widely used correlation coefficient identifying non-linear relationships between ordinal variables. In this paper, we investigated a parallel algorithm accelerating all-pairs Kendall's tau coefficient computation via single instruction multiple data (SIMD) vectorized sorting on Intel Xeon Phis by taking advantage of many processing cores and 512-bit SIMD vector instructions. To facilitate workload balancing and overcome on-chip memory limitation, we proposed a generic framework for symmetric all-pairs computation by building provable bijective functions between job identifier and coordinate space. Performance evaluation demonstrated that our algorithm on one 5110P Phi achieves two orders-of-magnitude speedups over 16-threaded MATLAB and three orders-of-magnitude speedups over sequential R, both running on high-end CPUs. Besides, our algorithm exhibited rather good distributed computing scalability with respect to number of Phis. Source code and datasets are publicly available at http://lightpcc.sourceforge.net.

A Parallel Algorithm for Exact Bayesian Structure Discovery in Bayesian Networks

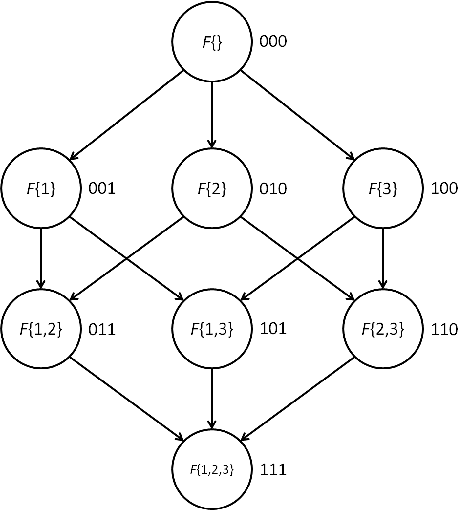
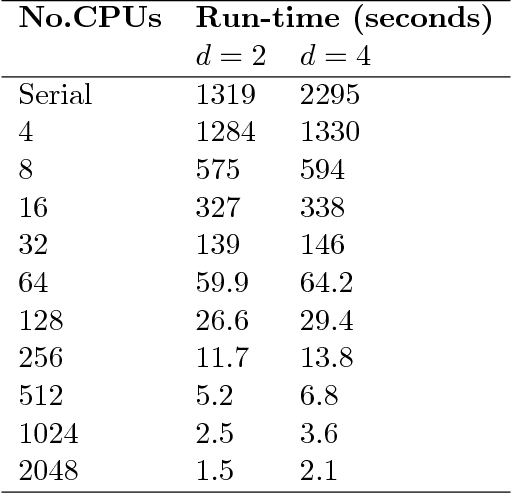
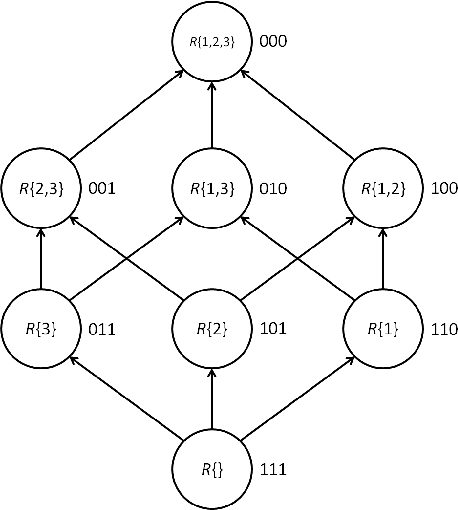
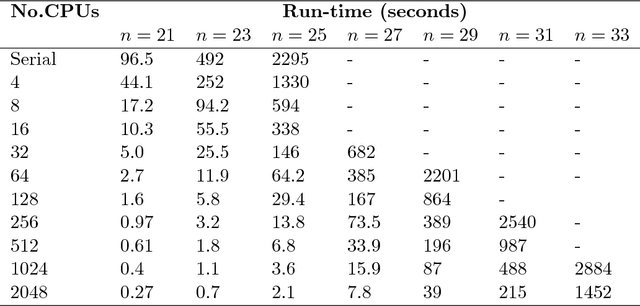
Exact Bayesian structure discovery in Bayesian networks requires exponential time and space. Using dynamic programming (DP), the fastest known sequential algorithm computes the exact posterior probabilities of structural features in $O(2(d+1)n2^n)$ time and space, if the number of nodes (variables) in the Bayesian network is $n$ and the in-degree (the number of parents) per node is bounded by a constant $d$. Here we present a parallel algorithm capable of computing the exact posterior probabilities for all $n(n-1)$ edges with optimal parallel space efficiency and nearly optimal parallel time efficiency. That is, if $p=2^k$ processors are used, the run-time reduces to $O(5(d+1)n2^{n-k}+k(n-k)^d)$ and the space usage becomes $O(n2^{n-k})$ per processor. Our algorithm is based the observation that the subproblems in the sequential DP algorithm constitute a $n$-$D$ hypercube. We take a delicate way to coordinate the computation of correlated DP procedures such that large amount of data exchange is suppressed. Further, we develop parallel techniques for two variants of the well-known \emph{zeta transform}, which have applications outside the context of Bayesian networks. We demonstrate the capability of our algorithm on datasets with up to 33 variables and its scalability on up to 2048 processors. We apply our algorithm to a biological data set for discovering the yeast pheromone response pathways.