Multi-Label Learning to Rank through Multi-Objective Optimization

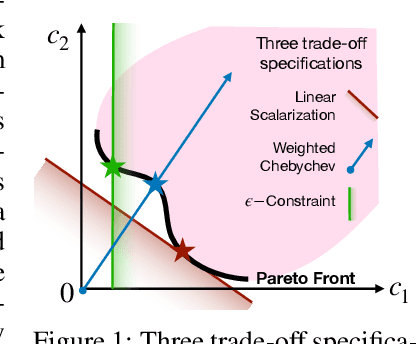
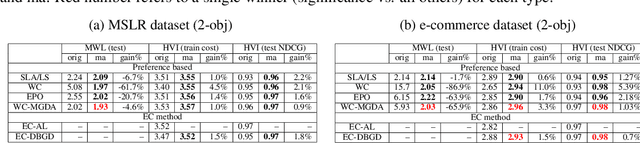
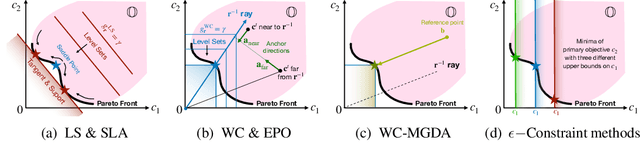
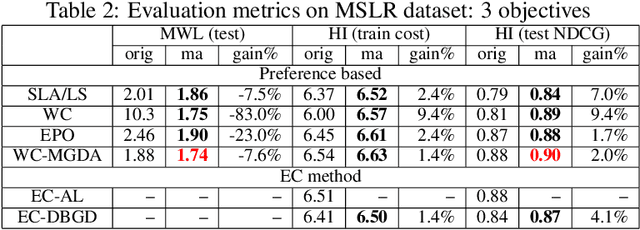
Learning to Rank (LTR) technique is ubiquitous in the Information Retrieval system nowadays, especially in the Search Ranking application. The query-item relevance labels typically used to train the ranking model are often noisy measurements of human behavior, e.g., product rating for product search. The coarse measurements make the ground truth ranking non-unique with respect to a single relevance criterion. To resolve ambiguity, it is desirable to train a model using many relevance criteria, giving rise to Multi-Label LTR (MLLTR). Moreover, it formulates multiple goals that may be conflicting yet important to optimize for simultaneously, e.g., in product search, a ranking model can be trained based on product quality and purchase likelihood to increase revenue. In this research, we leverage the Multi-Objective Optimization (MOO) aspect of the MLLTR problem and employ recently developed MOO algorithms to solve it. Specifically, we propose a general framework where the information from labels can be combined in a variety of ways to meaningfully characterize the trade-off among the goals. Our framework allows for any gradient based MOO algorithm to be used for solving the MLLTR problem. We test the proposed framework on two publicly available LTR datasets and one e-commerce dataset to show its efficacy.

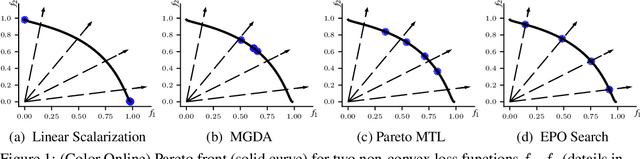
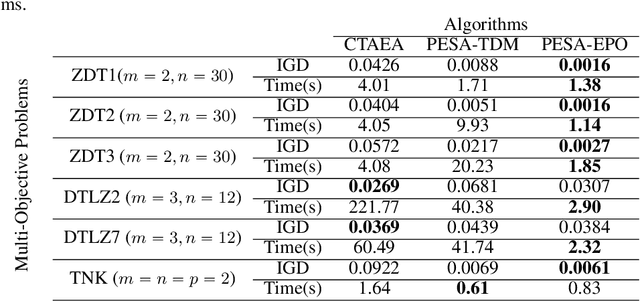
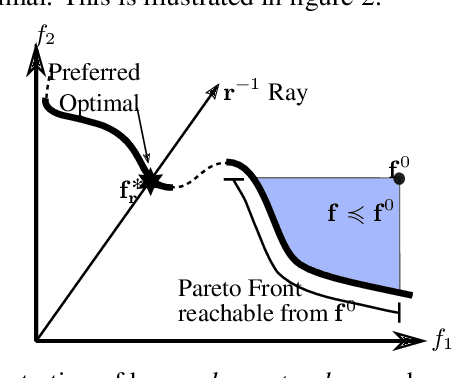
Exact Pareto Optimal Search for Multi-Task Learning: Touring the Pareto Front

Multi-Task Learning (MTL) is a well-established paradigm for training deep neural network models for multiple correlated tasks. Often the task objectives conflict, requiring trade-offs between them during model building. In such cases, MTL models can use gradient-based multi-objective optimization (MOO) to find one or more Pareto optimal solutions. A common requirement in MTL applications is to find an {\it Exact} Pareto optimal (EPO) solution, which satisfies user preferences with respect to task-specific objective functions. Further, to improve model generalization, various constraints on the weights may need to be enforced during training. Addressing these requirements is challenging because it requires a search direction that allows descent not only towards the Pareto front but also towards the input preference, within the constraints imposed and in a manner that scales to high-dimensional gradients. We design and theoretically analyze such search directions and develop the first scalable algorithm, with theoretical guarantees of convergence, to find an EPO solution, including when box and equality constraints are imposed. Our unique method combines multiple gradient descent with carefully controlled ascent to traverse the Pareto front in a principled manner, making it robust to initialization. This also facilitates systematic exploration of the Pareto front, that we utilize to approximate the Pareto front for multi-criteria decision-making. Empirical results show that our algorithm outperforms competing methods on benchmark MTL datasets and MOO problems.

Deep Sparse Coding Using Optimized Linear Expansion of Thresholds

We address the problem of reconstructing sparse signals from noisy and compressive measurements using a feed-forward deep neural network (DNN) with an architecture motivated by the iterative shrinkage-thresholding algorithm (ISTA). We maintain the weights and biases of the network links as prescribed by ISTA and model the nonlinear activation function using a linear expansion of thresholds (LET), which has been very successful in image denoising and deconvolution. The optimal set of coefficients of the parametrized activation is learned over a training dataset containing measurement-sparse signal pairs, corresponding to a fixed sensing matrix. For training, we develop an efficient second-order algorithm, which requires only matrix-vector product computations in every training epoch (Hessian-free optimization) and offers superior convergence performance than gradient-descent optimization. Subsequently, we derive an improved network architecture inspired by FISTA, a faster version of ISTA, to achieve similar signal estimation performance with about 50% of the number of layers. The resulting architecture turns out to be a deep residual network, which has recently been shown to exhibit superior performance in several visual recognition tasks. Numerical experiments demonstrate that the proposed DNN architectures lead to 3 to 4 dB improvement in the reconstruction signal-to-noise ratio (SNR), compared with the state-of-the-art sparse coding algorithms.