Neuromorphic Sampling of Sparse Signals

Neuromorphic sampling is a bioinspired and opportunistic analog-to-digital conversion technique, where the measurements are recorded only when there is a significant change in the signal amplitude. Neuromorphic sampling has paved the way for a new class of vision sensors called event cameras or dynamic vision sensors (DVS), which consume low power, accommodate a high-dynamic range, and provide sparse measurements with high temporal resolution making it convenient for downstream inference tasks. In this paper, we consider neuromorphic sensing of signals with a finite rate of innovation (FRI), including a stream of Dirac impulses, sum of weighted and time-shifted pulses, and piecewise-polynomial functions. We consider a sampling-theoretic approach and leverage the close connection between neuromorphic sensing and time-based sampling, where the measurements are encoded temporally. Using Fourier-domain analysis, we show that perfect signal reconstruction is possible via parameter estimation using high-resolution spectral estimation methods. We develop a kernel-based sampling approach, which allows for perfect reconstruction with a sample complexity equal to the rate of innovation of the signal. We provide sufficient conditions on the parameters of the neuromorphic encoder for perfect reconstruction. Furthermore, we extend the analysis to multichannel neuromorphic sampling of FRI signals, in the single-input multi-output (SIMO) and multi-input multi-output (MIMO) configurations. We show that the signal parameters can be jointly estimated using multichannel measurements. Experimental results are provided to substantiate the theoretical claims.

Tight-frame-like Sparse Recovery Using Non-tight Sensing Matrices

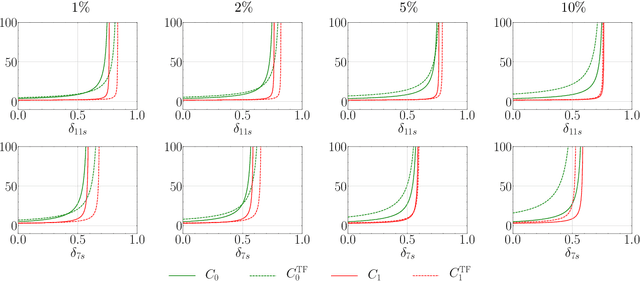
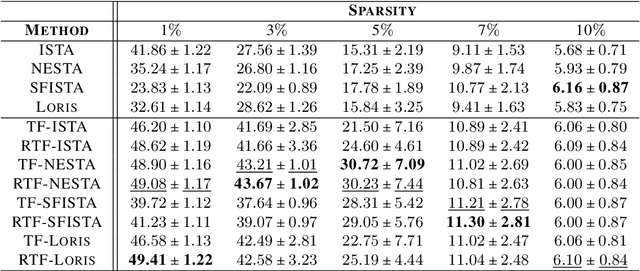
The choice of the sensing matrix is crucial in compressed sensing (CS). Gaussian sensing matrices possess the desirable restricted isometry property (RIP), which is crucial for providing performance guarantees on sparse recovery. Further, sensing matrices that constitute a Parseval tight frame result in minimum mean-squared-error (MSE) reconstruction given oracle knowledge of the support of the sparse vector. However, if the sensing matrix is not tight, could one achieve the reconstruction performance assured by a tight frame by suitably designing the reconstruction strategy? This is the key question that we address in this paper. We develop a novel formulation that relies on a generalized l2-norm-based data-fidelity loss that tightens the sensing matrix, along with the standard l1 penalty for enforcing sparsity. The optimization is performed using proximal gradient method, resulting in the tight-frame iterative shrinkage thresholding algorithm (TF-ISTA). We show that the objective convergence of TF-ISTA is linear akin to that of ISTA. Incorporating Nesterovs momentum into TF-ISTA results in a faster variant, namely, TF-FISTA, whose objective convergence is quadratic, akin to that of FISTA. We provide performance guarantees on the l2-error for the proposed formulation. Experimental results show that the proposed algorithms offer superior sparse recovery performance and faster convergence. Proceeding further, we develop the network variants of TF-ISTA and TF-FISTA, wherein a convolutional neural network is used as the sparsifying operator. On the application front, we consider compressed sensing image recovery (CSIR). Experimental results on Set11, BSD68, Urban100, and DIV2K datasets show that the proposed models outperform state-of-the-art sparse recovery methods, with performance measured in terms of peak signal-to-noise ratio (PSNR) and structural similarity index metric (SSIM).

Neuromorphic Sampling of Signals in Shift-Invariant Spaces

Neuromorphic sampling is a paradigm shift in analog-to-digital conversion where the acquisition strategy is opportunistic and measurements are recorded only when there is a significant change in the signal. Neuromorphic sampling has given rise to a new class of event-based sensors called dynamic vision sensors or neuromorphic cameras. The neuromorphic sampling mechanism utilizes low power and provides high-dynamic range sensing with low latency and high temporal resolution. The measurements are sparse and have low redundancy making it convenient for downstream tasks. In this paper, we present a sampling-theoretic perspective to neuromorphic sensing of continuous-time signals. We establish a close connection between neuromorphic sampling and time-based sampling - where signals are encoded temporally. We analyse neuromorphic sampling of signals in shift-invariant spaces, in particular, bandlimited signals and polynomial splines. We present an iterative technique for perfect reconstruction subject to the events satisfying a density criterion. We also provide necessary and sufficient conditions for perfect reconstruction. Owing to practical limitations in meeting the sufficient conditions for perfect reconstruction, we extend the analysis to approximate reconstruction from sparse events. In the latter setting, we pose signal reconstruction as a continuous-domain linear inverse problem whose solution can be obtained by solving an equivalent finite-dimensional convex optimization program using a variable-splitting approach. We demonstrate the performance of the proposed algorithm and validate our claims via experiments on synthetic signals.

GANs Settle Scores!

Generative adversarial networks (GANs) comprise a generator, trained to learn the underlying distribution of the desired data, and a discriminator, trained to distinguish real samples from those output by the generator. A majority of GAN literature focuses on understanding the optimality of the discriminator through integral probability metric (IPM) or divergence based analysis. In this paper, we propose a unified approach to analyzing the generator optimization through variational approach. In $f$-divergence-minimizing GANs, we show that the optimal generator is the one that matches the score of its output distribution with that of the data distribution, while in IPM GANs, we show that this optimal generator matches score-like functions, involving the flow-field of the kernel associated with a chosen IPM constraint space. Further, the IPM-GAN optimization can be seen as one of smoothed score-matching, where the scores of the data and the generator distributions are convolved with the kernel associated with the constraint. The proposed approach serves to unify score-based training and existing GAN flavors, leveraging results from normalizing flows, while also providing explanations for empirical phenomena such as the stability of non-saturating GAN losses. Based on these results, we propose novel alternatives to $f$-GAN and IPM-GAN training based on score and flow matching, and discriminator-guided Langevin sampling.

Data Interpolants -- That's What Discriminators in Higher-order Gradient-regularized GANs Are

We consider the problem of optimizing the discriminator in generative adversarial networks (GANs) subject to higher-order gradient regularization. We show analytically, via the least-squares (LSGAN) and Wasserstein (WGAN) GAN variants, that the discriminator optimization problem is one of interpolation in $n$-dimensions. The optimal discriminator, derived using variational Calculus, turns out to be the solution to a partial differential equation involving the iterated Laplacian or the polyharmonic operator. The solution is implementable in closed-form via polyharmonic radial basis function (RBF) interpolation. In view of the polyharmonic connection, we refer to the corresponding GANs as Poly-LSGAN and Poly-WGAN. Through experimental validation on multivariate Gaussians, we show that implementing the optimal RBF discriminator in closed-form, with penalty orders $m \approx\lceil \frac{n}{2} \rceil $, results in superior performance, compared to training GAN with arbitrarily chosen discriminator architectures. We employ the Poly-WGAN discriminator to model the latent space distribution of the data with encoder-decoder-based GAN flavors such as Wasserstein autoencoders.

Spider GAN: Leveraging Friendly Neighbors to Accelerate GAN Training

Training Generative adversarial networks (GANs) stably is a challenging task. The generator in GANs transform noise vectors, typically Gaussian distributed, into realistic data such as images. In this paper, we propose a novel approach for training GANs with images as inputs, but without enforcing any pairwise constraints. The intuition is that images are more structured than noise, which the generator can leverage to learn a more robust transformation. The process can be made efficient by identifying closely related datasets, or a ``friendly neighborhood'' of the target distribution, inspiring the moniker, Spider GAN. To define friendly neighborhoods leveraging proximity between datasets, we propose a new measure called the signed inception distance (SID), inspired by the polyharmonic kernel. We show that the Spider GAN formulation results in faster convergence, as the generator can discover correspondence even between seemingly unrelated datasets, for instance, between Tiny-ImageNet and CelebA faces. Further, we demonstrate cascading Spider GAN, where the output distribution from a pre-trained GAN generator is used as the input to the subsequent network. Effectively, transporting one distribution to another in a cascaded fashion until the target is learnt -- a new flavor of transfer learning. We demonstrate the efficacy of the Spider approach on DCGAN, conditional GAN, PGGAN, StyleGAN2 and StyleGAN3. The proposed approach achieves state-of-the-art Frechet inception distance (FID) values, with one-fifth of the training iterations, in comparison to their baseline counterparts on high-resolution small datasets such as MetFaces, Ukiyo-E Faces and AFHQ-Cats.

Time Encoding of Finite-Rate-of-Innovation Signals

Time-encoding of continuous-time signals is an alternative sampling paradigm to conventional methods such as Shannon's sampling. In time-encoding, the signal is encoded using a sequence of time instants where an event occurs, and hence fall under event-driven sampling methods. Time-encoding can be designed agnostic to the global clock of the sampling hardware, which makes sampling asynchronous. Moreover, the encoding is sparse. This makes time-encoding energy efficient. However, the signal representation is nonstandard and in general, nonuniform. In this paper, we consider time-encoding of finite-rate-of-innovation signals, and in particular, periodic signals composed of weighted and time-shifted versions of a known pulse. We consider encoding using both crossing-time-encoding machine (C-TEM) and integrate-and-fire time-encoding machine (IF-TEM). We analyze how time-encoding manifests in the Fourier domain and arrive at the familiar sum-of-sinusoids structure of the Fourier coefficients that can be obtained starting from the time-encoded measurements via a suitable linear transformation. Thereafter, standard FRI techniques become applicable. Further, we extend the theory to multichannel time-encoding such that each channel operates with a lower sampling requirement. We also study the effect of measurement noise, where the temporal measurements are perturbed by additive noise. To combat the effect of noise, we propose a robust optimization framework to simultaneously denoise the Fourier coefficients and estimate the annihilating filter accurately. We provide sufficient conditions for time-encoding and perfect reconstruction using C-TEM and IF-TEM, and furnish extensive simulations to substantiate our findings.

Wavelet Design in a Learning Framework

Wavelets have proven to be highly successful in several signal and image processing applications. Wavelet design has been an active field of research for over two decades, with the problem often being approached from an analytical perspective. In this paper, we introduce a learning based approach to wavelet design. We draw a parallel between convolutional autoencoders and wavelet multiresolution approximation, and show how the learning angle provides a coherent computational framework for addressing the design problem. We aim at designing data-independent wavelets by training filterbank autoencoders, which precludes the need for customized datasets. In fact, we use high-dimensional Gaussian vectors for training filterbank autoencoders, and show that a near-zero training loss implies that the learnt filters satisfy the perfect reconstruction property with very high probability. Properties of a wavelet such as orthogonality, compact support, smoothness, symmetry, and vanishing moments can be incorporated by designing the autoencoder architecture appropriately and with a suitable regularization term added to the mean-squared error cost used in the learning process. Our approach not only recovers the well known Daubechies family of orthogonal wavelets and the Cohen-Daubechies-Feauveau family of symmetric biorthogonal wavelets, but also learns wavelets outside these families.

Learning Generative Prior with Latent Space Sparsity Constraints

We address the problem of compressed sensing using a deep generative prior model and consider both linear and learned nonlinear sensing mechanisms, where the nonlinear one involves either a fully connected neural network or a convolutional neural network. Recently, it has been argued that the distribution of natural images do not lie in a single manifold but rather lie in a union of several submanifolds. We propose a sparsity-driven latent space sampling (SDLSS) framework and develop a proximal meta-learning (PML) algorithm to enforce sparsity in the latent space. SDLSS allows the range-space of the generator to be considered as a union-of-submanifolds. We also derive the sample complexity bounds within the SDLSS framework for the linear measurement model. The results demonstrate that for a higher degree of compression, the SDLSS method is more efficient than the state-of-the-art method. We first consider a comparison between linear and nonlinear sensing mechanisms on Fashion-MNIST dataset and show that the learned nonlinear version is superior to the linear one. Subsequent comparisons with the deep compressive sensing (DCS) framework proposed in the literature are reported. We also consider the effect of the dimension of the latent space and the sparsity factor in validating the SDLSS framework. Performance quantification is carried out by employing three objective metrics: peak signal-to-noise ratio (PSNR), structural similarity index metric (SSIM), and reconstruction error (RE).

Quantized Proximal Averaging Network for Analysis Sparse Coding

We solve the analysis sparse coding problem considering a combination of convex and non-convex sparsity promoting penalties. The multi-penalty formulation results in an iterative algorithm involving proximal-averaging. We then unfold the iterative algorithm into a trainable network that facilitates learning the sparsity prior. We also consider quantization of the network weights. Quantization makes neural networks efficient both in terms of memory and computation during inference, and also renders them compatible for low-precision hardware deployment. Our learning algorithm is based on a variant of the ADAM optimizer in which the quantizer is part of the forward pass and the gradients of the loss function are evaluated corresponding to the quantized weights while doing a book-keeping of the high-precision weights. We demonstrate applications to compressed image recovery and magnetic resonance image reconstruction. The proposed approach offers superior reconstruction accuracy and quality than state-of-the-art unfolding techniques and the performance degradation is minimal even when the weights are subjected to extreme quantization.