Tight-frame-like Sparse Recovery Using Non-tight Sensing Matrices

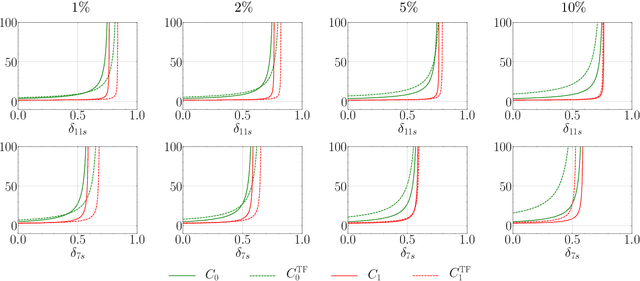
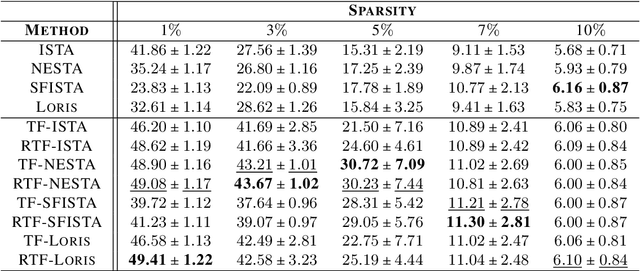
The choice of the sensing matrix is crucial in compressed sensing (CS). Gaussian sensing matrices possess the desirable restricted isometry property (RIP), which is crucial for providing performance guarantees on sparse recovery. Further, sensing matrices that constitute a Parseval tight frame result in minimum mean-squared-error (MSE) reconstruction given oracle knowledge of the support of the sparse vector. However, if the sensing matrix is not tight, could one achieve the reconstruction performance assured by a tight frame by suitably designing the reconstruction strategy? This is the key question that we address in this paper. We develop a novel formulation that relies on a generalized l2-norm-based data-fidelity loss that tightens the sensing matrix, along with the standard l1 penalty for enforcing sparsity. The optimization is performed using proximal gradient method, resulting in the tight-frame iterative shrinkage thresholding algorithm (TF-ISTA). We show that the objective convergence of TF-ISTA is linear akin to that of ISTA. Incorporating Nesterovs momentum into TF-ISTA results in a faster variant, namely, TF-FISTA, whose objective convergence is quadratic, akin to that of FISTA. We provide performance guarantees on the l2-error for the proposed formulation. Experimental results show that the proposed algorithms offer superior sparse recovery performance and faster convergence. Proceeding further, we develop the network variants of TF-ISTA and TF-FISTA, wherein a convolutional neural network is used as the sparsifying operator. On the application front, we consider compressed sensing image recovery (CSIR). Experimental results on Set11, BSD68, Urban100, and DIV2K datasets show that the proposed models outperform state-of-the-art sparse recovery methods, with performance measured in terms of peak signal-to-noise ratio (PSNR) and structural similarity index metric (SSIM).