Bandit Learning to Rank with Position-Based Click Models: Personalized and Equal Treatments
Paper and Code
Nov 08, 2023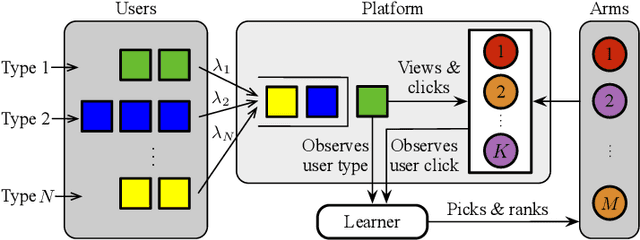
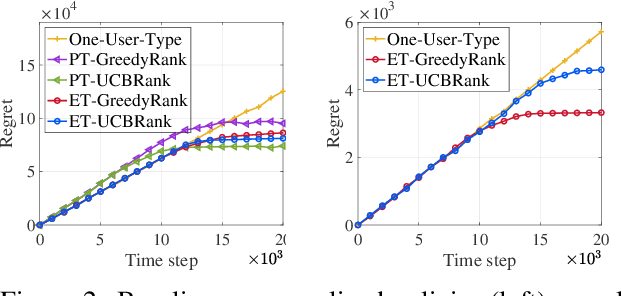

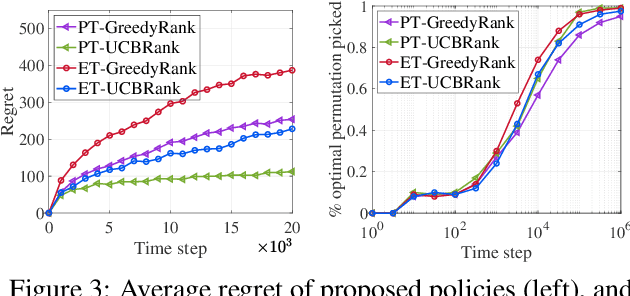
Online learning to rank (ONL2R) is a foundational problem for recommender systems and has received increasing attention in recent years. Among the existing approaches for ONL2R, a natural modeling architecture is the multi-armed bandit framework coupled with the position-based click model. However, developing efficient online learning policies for MAB-based ONL2R with position-based click models is highly challenging due to the combinatorial nature of the problem, and partial observability in the position-based click model. To date, results in MAB-based ONL2R with position-based click models remain rather limited, which motivates us to fill this gap in this work. Our main contributions in this work are threefold: i) We propose the first general MAB framework that captures all key ingredients of ONL2R with position-based click models. Our model considers personalized and equal treatments in ONL2R ranking recommendations, both of which are widely used in practice; ii) Based on the above analytical framework, we develop two unified greed- and UCB-based policies called GreedyRank and UCBRank, each of which can be applied to personalized and equal ranking treatments; and iii) We show that both GreedyRank and UCBRank enjoy $O(\sqrt{t}\ln t)$ and $O(\sqrt{t\ln t})$ anytime sublinear regret for personalized and equal treatment, respectively. For the fundamentally hard equal ranking treatment, we identify classes of collective utility functions and their associated sufficient conditions under which $O(\sqrt{t}\ln t)$ and $O(\sqrt{t\ln t})$ anytime sublinear regrets are still achievable for GreedyRank and UCBRank, respectively. Our numerical experiments also verify our theoretical results and demonstrate the efficiency of GreedyRank and UCBRank in seeking the optimal action under various problem settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge