Extreme Multi-label Classification from Aggregated Labels

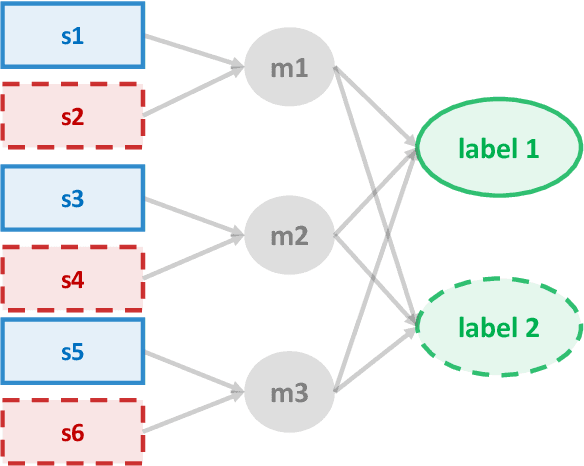
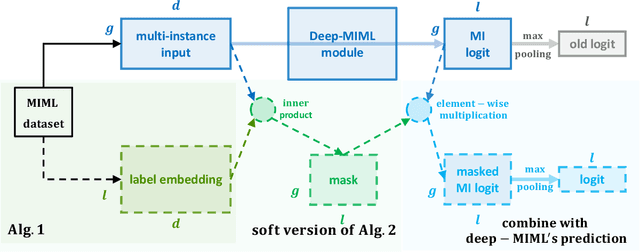
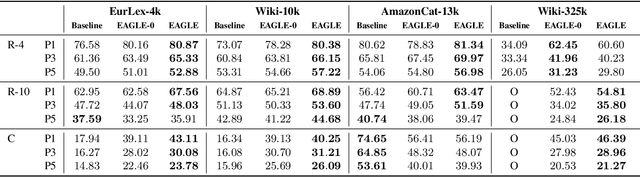
Extreme multi-label classification (XMC) is the problem of finding the relevant labels for an input, from a very large universe of possible labels. We consider XMC in the setting where labels are available only for groups of samples - but not for individual ones. Current XMC approaches are not built for such multi-instance multi-label (MIML) training data, and MIML approaches do not scale to XMC sizes. We develop a new and scalable algorithm to impute individual-sample labels from the group labels; this can be paired with any existing XMC method to solve the aggregated label problem. We characterize the statistical properties of our algorithm under mild assumptions, and provide a new end-to-end framework for MIML as an extension. Experiments on both aggregated label XMC and MIML tasks show the advantages over existing approaches.

Interaction Hard Thresholding: Consistent Sparse Quadratic Regression in Sub-quadratic Time and Space

Quadratic regression involves modeling the response as a (generalized) linear function of not only the features $x^{j_1}$ but also of quadratic terms $x^{j_1}x^{j_2}$. The inclusion of such higher-order "interaction terms" in regression often provides an easy way to increase accuracy in already-high-dimensional problems. However, this explodes the problem dimension from linear $O(p)$ to quadratic $O(p^2)$, and it is common to look for sparse interactions (typically via heuristics). In this paper, we provide a new algorithm - Interaction Hard Thresholding (IntHT) which is the first one to provably accurately solve this problem in sub-quadratic time and space. It is a variant of Iterative Hard Thresholding; one that uses the special quadratic structure to devise a new way to (approx.) extract the top elements of a $p^2$ size gradient in sub-$p^2$ time and space. Our main result is to theoretically prove that, in spite of the many speedup-related approximations, IntHT linearly converges to a consistent estimate under standard high-dimensional sparse recovery assumptions. We also demonstrate its value via synthetic experiments. Moreover, we numerically show that IntHT can be extended to higher-order regression problems, and also theoretically analyze an SVRG variant of IntHT.

Iterative Least Trimmed Squares for Mixed Linear Regression

Given a linear regression setting, Iterative Least Trimmed Squares (ILTS) involves alternating between (a) selecting the subset of samples with lowest current loss, and (b) re-fitting the linear model only on that subset. Both steps are very fast and simple. In this paper we analyze ILTS in the setting of mixed linear regression with corruptions (MLR-C). We first establish deterministic conditions (on the features etc.) under which the ILTS iterate converges linearly to the closest mixture component. We also provide a global algorithm that uses ILTS as a subroutine, to fully solve mixed linear regressions with corruptions. We then evaluate it for the widely studied setting of isotropic Gaussian features, and establish that we match or better existing results in terms of sample complexity. Finally, we provide an ODE analysis for a gradient-descent variant of ILTS that has optimal time complexity. Our results provide initial theoretical evidence that iteratively fitting to the best subset of samples -- a potentially widely applicable idea -- can provably provide state of the art performance in bad training data settings.

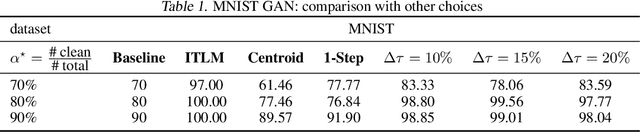
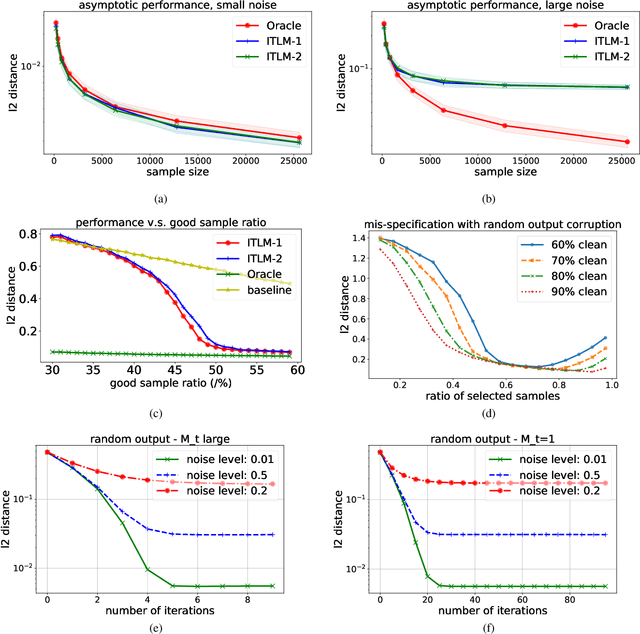
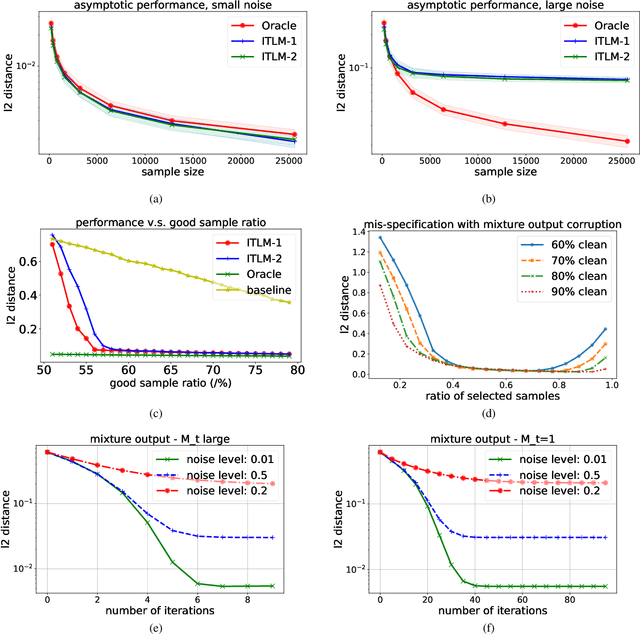
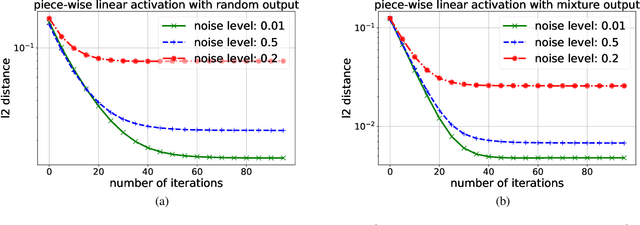
Iteratively Learning from the Best

We study a simple generic framework to address the issue of bad training data; both bad labels in supervised problems, and bad samples in unsupervised ones. Our approach starts by fitting a model to the whole training dataset, but then iteratively improves it by alternating between (a) revisiting the training data to select samples with lowest current loss, and (b) re-training the model on only these selected samples. It can be applied to any existing model training setting which provides a loss measure for samples, and a way to refit on new ones. We show the merit of this approach in both theory and practice. We first prove statistical consistency, and linear convergence to the ground truth and global optimum, for two simpler model settings: mixed linear regression, and gaussian mixture models. We then demonstrate its success empirically in (a) saving the accuracy of existing deep image classifiers when there are errors in the labels of training images, and (b) improving the quality of samples generated by existing DC-GAN models, when it is given training data that contains a fraction of the images from a different and unintended dataset. The experimental results show significant improvement over the baseline methods that ignore the existence of bad labels/samples.

Dense Information Flow for Neural Machine Translation

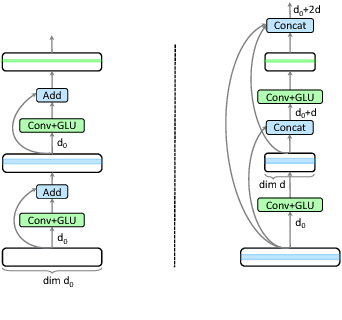
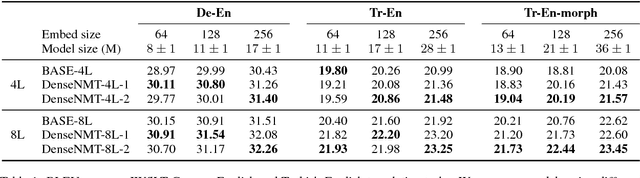
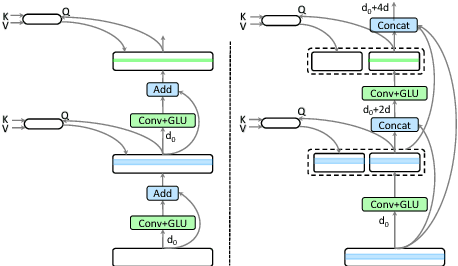
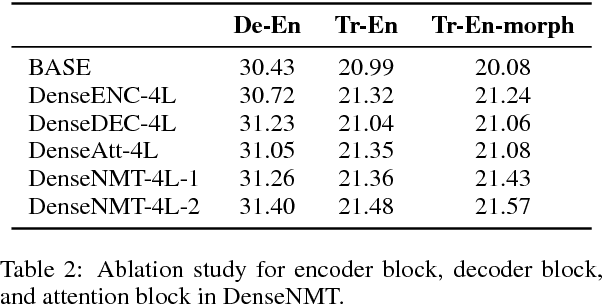
Recently, neural machine translation has achieved remarkable progress by introducing well-designed deep neural networks into its encoder-decoder framework. From the optimization perspective, residual connections are adopted to improve learning performance for both encoder and decoder in most of these deep architectures, and advanced attention connections are applied as well. Inspired by the success of the DenseNet model in computer vision problems, in this paper, we propose a densely connected NMT architecture (DenseNMT) that is able to train more efficiently for NMT. The proposed DenseNMT not only allows dense connection in creating new features for both encoder and decoder, but also uses the dense attention structure to improve attention quality. Our experiments on multiple datasets show that DenseNMT structure is more competitive and efficient.

High Dimensional Robust Sparse Regression

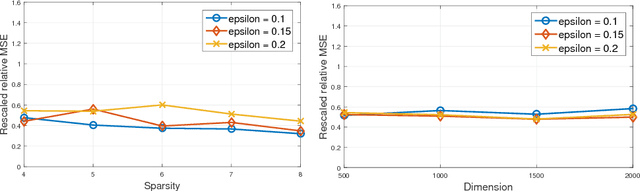
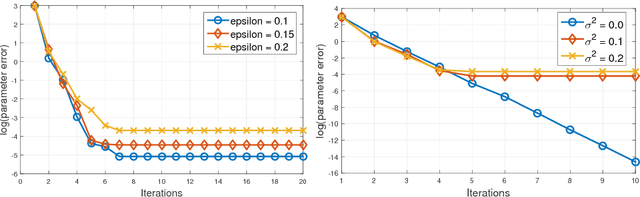
We provide a novel -- and to the best of our knowledge, the first -- algorithm for high dimensional sparse regression with corruptions in explanatory and/or response variables. Our algorithm recovers the true sparse parameters in the presence of a constant fraction of arbitrary corruptions. Our main contribution is a robust variant of Iterative Hard Thresholding. Using this, we provide accurate estimators with sub-linear sample complexity. Our algorithm consists of a novel randomized outlier removal technique for robust sparse mean estimation that may be of interest in its own right: it is orderwise more efficient computationally than existing algorithms, and succeeds with high probability, thus making it suitable for general use in iterative algorithms. We demonstrate the effectiveness on large-scale sparse regression problems with arbitrary corruptions.

Deep Active Learning for Named Entity Recognition

Deep learning has yielded state-of-the-art performance on many natural language processing tasks including named entity recognition (NER). However, this typically requires large amounts of labeled data. In this work, we demonstrate that the amount of labeled training data can be drastically reduced when deep learning is combined with active learning. While active learning is sample-efficient, it can be computationally expensive since it requires iterative retraining. To speed this up, we introduce a lightweight architecture for NER, viz., the CNN-CNN-LSTM model consisting of convolutional character and word encoders and a long short term memory (LSTM) tag decoder. The model achieves nearly state-of-the-art performance on standard datasets for the task while being computationally much more efficient than best performing models. We carry out incremental active learning, during the training process, and are able to nearly match state-of-the-art performance with just 25\% of the original training data.