Statistical Guarantees Of False Discovery Rate In Medical Instance Segmentation Tasks Based on Conformal Risk Control

Instance segmentation plays a pivotal role in medical image analysis by enabling precise localization and delineation of lesions, tumors, and anatomical structures. Although deep learning models such as Mask R-CNN and BlendMask have achieved remarkable progress, their application in high-risk medical scenarios remains constrained by confidence calibration issues, which may lead to misdiagnosis. To address this challenge, we propose a robust quality control framework based on conformal prediction theory. This framework innovatively constructs a risk-aware dynamic threshold mechanism that adaptively adjusts segmentation decision boundaries according to clinical requirements.Specifically, we design a \textbf{calibration-aware loss function} that dynamically tunes the segmentation threshold based on a user-defined risk level $\alpha$. Utilizing exchangeable calibration data, this method ensures that the expected FNR or FDR on test data remains below $\alpha$ with high probability. The framework maintains compatibility with mainstream segmentation models (e.g., Mask R-CNN, BlendMask+ResNet-50-FPN) and datasets (PASCAL VOC format) without requiring architectural modifications. Empirical results demonstrate that we rigorously bound the FDR metric marginally over the test set via our developed calibration framework.

Prompt Learning for Oriented Power Transmission Tower Detection in High-Resolution SAR Images

Detecting transmission towers from synthetic aperture radar (SAR) images remains a challenging task due to the comparatively small size and side-looking geometry, with background clutter interference frequently hindering tower identification. A large number of interfering signals superimposes the return signal from the tower. We found that localizing or prompting positions of power transmission towers is beneficial to address this obstacle. Based on this revelation, this paper introduces prompt learning into the oriented object detector (P2Det) for multimodal information learning. P2Det contains the sparse prompt coding and cross-attention between the multimodal data. Specifically, the sparse prompt encoder (SPE) is proposed to represent point locations, converting prompts into sparse embeddings. The image embeddings are generated through the Transformer layers. Then a two-way fusion module (TWFM) is proposed to calculate the cross-attention of the two different embeddings. The interaction of image-level and prompt-level features is utilized to address the clutter interference. A shape-adaptive refinement module (SARM) is proposed to reduce the effect of aspect ratio. Extensive experiments demonstrated the effectiveness of the proposed model on high-resolution SAR images. P2Det provides a novel insight for multimodal object detection due to its competitive performance.

Learning Deep Implicit Functions for 3D Shapes with Dynamic Code Clouds

Deep Implicit Function (DIF) has gained popularity as an efficient 3D shape representation. To capture geometry details, current methods usually learn DIF using local latent codes, which discretize the space into a regular 3D grid (or octree) and store local codes in grid points (or octree nodes). Given a query point, the local feature is computed by interpolating its neighboring local codes with their positions. However, the local codes are constrained at discrete and regular positions like grid points, which makes the code positions difficult to be optimized and limits their representation ability. To solve this problem, we propose to learn DIF with Dynamic Code Cloud, named DCC-DIF. Our method explicitly associates local codes with learnable position vectors, and the position vectors are continuous and can be dynamically optimized, which improves the representation ability. In addition, we propose a novel code position loss to optimize the code positions, which heuristically guides more local codes to be distributed around complex geometric details. In contrast to previous methods, our DCC-DIF represents 3D shapes more efficiently with a small amount of local codes, and improves the reconstruction quality. Experiments demonstrate that DCC-DIF achieves better performance over previous methods. Code and data are available at https://github.com/lity20/DCCDIF.

Robust Screening of COVID-19 from Chest X-ray via Discriminative Cost-Sensitive Learning

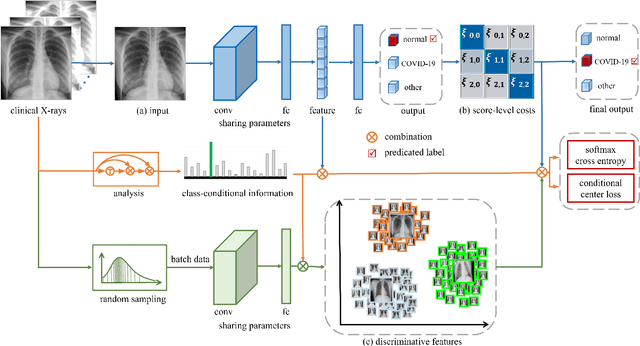
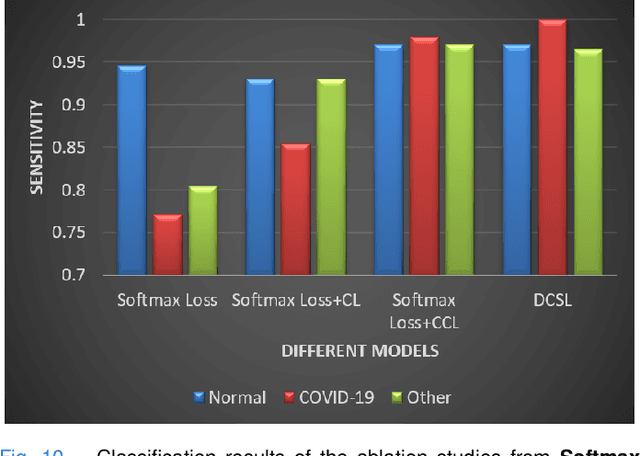
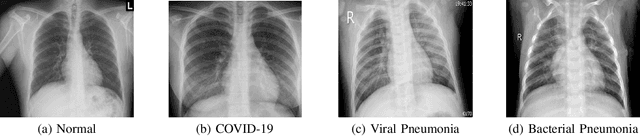
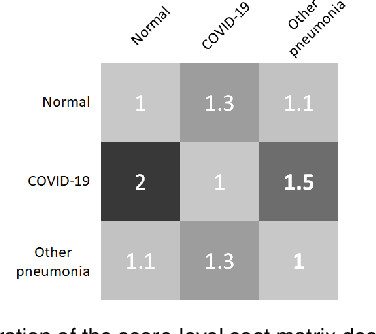
This paper addresses the new problem of automated screening of coronavirus disease 2019 (COVID-19) based on chest X-rays, which is urgently demanded toward fast stopping the pandemic. However, robust and accurate screening of COVID-19 from chest X-rays is still a globally recognized challenge because of two bottlenecks: 1) imaging features of COVID-19 share some similarities with other pneumonia on chest X-rays, and 2) the misdiagnosis rate of COVID-19 is very high, and the misdiagnosis cost is expensive. While a few pioneering works have made much progress, they underestimate both crucial bottlenecks. In this paper, we report our solution, discriminative cost-sensitive learning (DCSL), which should be the choice if the clinical needs the assisted screening of COVID-19 from chest X-rays. DCSL combines both advantages from fine-grained classification and cost-sensitive learning. Firstly, DCSL develops a conditional center loss that learns deep discriminative representation. Secondly, DCSL establishes score-level cost-sensitive learning that can adaptively enlarge the cost of misclassifying COVID-19 examples into other classes. DCSL is so flexible that it can apply in any deep neural network. We collected a large-scale multi-class dataset comprised of 2,239 chest X-ray examples: 239 examples from confirmed COVID-19 cases, 1,000 examples with confirmed bacterial or viral pneumonia cases, and 1,000 examples of healthy people. Extensive experiments on the three-class classification show that our algorithm remarkably outperforms state-of-the-art algorithms. It achieves an accuracy of 97.01%, a precision of 97%, a sensitivity of 97.09%, and an F1-score of 96.98%. These results endow our algorithm as an efficient tool for the fast large-scale screening of COVID-19.

Point Cloud Completion by Skip-attention Network with Hierarchical Folding

Point cloud completion aims to infer the complete geometries for missing regions of 3D objects from incomplete ones. Previous methods usually predict the complete point cloud based on the global shape representation extracted from the incomplete input. However, the global representation often suffers from the information loss of structure details on local regions of incomplete point cloud. To address this problem, we propose Skip-Attention Network (SA-Net) for 3D point cloud completion. Our main contributions lie in the following two-folds. First, we propose a skip-attention mechanism to effectively exploit the local structure details of incomplete point clouds during the inference of missing parts. The skip-attention mechanism selectively conveys geometric information from the local regions of incomplete point clouds for the generation of complete ones at different resolutions, where the skip-attention reveals the completion process in an interpretable way. Second, in order to fully utilize the selected geometric information encoded by skip-attention mechanism at different resolutions, we propose a novel structure-preserving decoder with hierarchical folding for complete shape generation. The hierarchical folding preserves the structure of complete point cloud generated in upper layer by progressively detailing the local regions, using the skip-attentioned geometry at the same resolution. We conduct comprehensive experiments on ShapeNet and KITTI datasets, which demonstrate that the proposed SA-Net outperforms the state-of-the-art point cloud completion methods.

High Dimensional Robust Estimation of Sparse Models via Trimmed Hard Thresholding

We study the problem of sparsity constrained $M$-estimation with arbitrary corruptions to both {\em explanatory and response} variables in the high-dimensional regime, where the number of variables $d$ is larger than the sample size $n$. Our main contribution is a highly efficient gradient-based optimization algorithm that we call Trimmed Hard Thresholding -- a robust variant of Iterative Hard Thresholding (IHT) by using trimmed mean in gradient computations. Our algorithm can deal with a wide class of sparsity constrained $M$-estimation problems, and we can tolerate a nearly dimension independent fraction of arbitrarily corrupted samples. More specifically, when the corrupted fraction satisfies $\epsilon \lesssim {1} /\left({\sqrt{k} \log (nd)}\right)$, where $k$ is the sparsity of the parameter, we obtain accurate estimation and model selection guarantees with optimal sample complexity. Furthermore, we extend our algorithm to sparse Gaussian graphical model (precision matrix) estimation via a neighborhood selection approach. We demonstrate the effectiveness of robust estimation in sparse linear, logistic regression, and sparse precision matrix estimation on synthetic and real-world US equities data.

High Dimensional Robust Sparse Regression

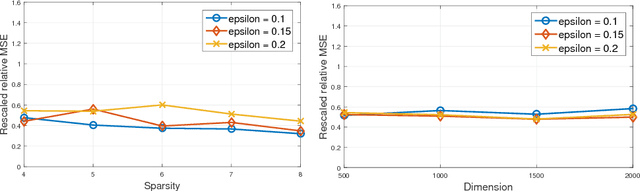
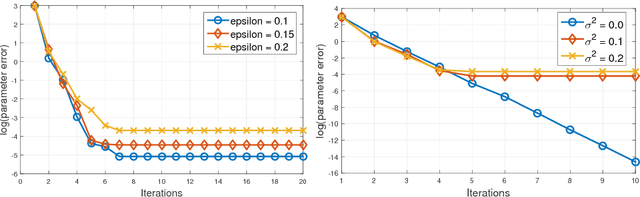
We provide a novel -- and to the best of our knowledge, the first -- algorithm for high dimensional sparse regression with corruptions in explanatory and/or response variables. Our algorithm recovers the true sparse parameters in the presence of a constant fraction of arbitrary corruptions. Our main contribution is a robust variant of Iterative Hard Thresholding. Using this, we provide accurate estimators with sub-linear sample complexity. Our algorithm consists of a novel randomized outlier removal technique for robust sparse mean estimation that may be of interest in its own right: it is orderwise more efficient computationally than existing algorithms, and succeeds with high probability, thus making it suitable for general use in iterative algorithms. We demonstrate the effectiveness on large-scale sparse regression problems with arbitrary corruptions.

Approximate Newton-based statistical inference using only stochastic gradients

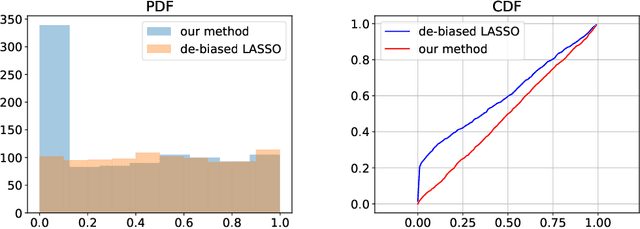
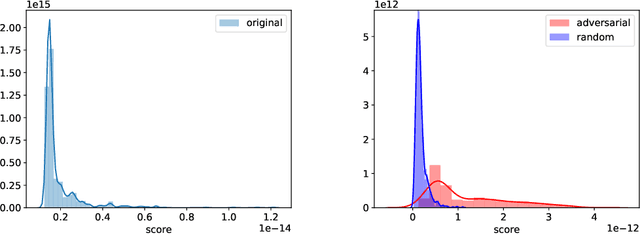
We present a novel inference framework for convex empirical risk minimization, using approximate stochastic Newton steps. The proposed algorithm is based on the notion of finite differences and allows the approximation of a Hessian-vector product from first-order information. In theory, our method efficiently computes the statistical error covariance in $M$-estimation, both for unregularized convex learning problems and high-dimensional LASSO regression, without using exact second order information, or resampling the entire data set. In practice, we demonstrate the effectiveness of our framework on large-scale machine learning problems, that go even beyond convexity: as a highlight, our work can be used to detect certain adversarial attacks on neural networks.

Statistical inference using SGD

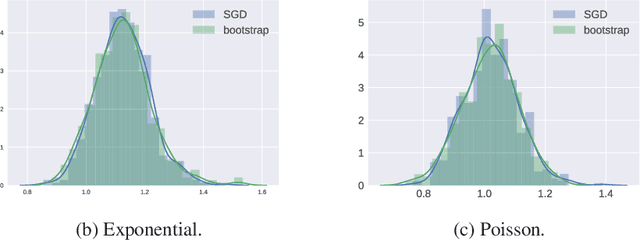
We present a novel method for frequentist statistical inference in $M$-estimation problems, based on stochastic gradient descent (SGD) with a fixed step size: we demonstrate that the average of such SGD sequences can be used for statistical inference, after proper scaling. An intuitive analysis using the Ornstein-Uhlenbeck process suggests that such averages are asymptotically normal. From a practical perspective, our SGD-based inference procedure is a first order method, and is well-suited for large scale problems. To show its merits, we apply it to both synthetic and real datasets, and demonstrate that its accuracy is comparable to classical statistical methods, while requiring potentially far less computation.