Learning Bijective Surface Parameterization for Inferring Signed Distance Functions from Sparse Point Clouds with Grid Deformation

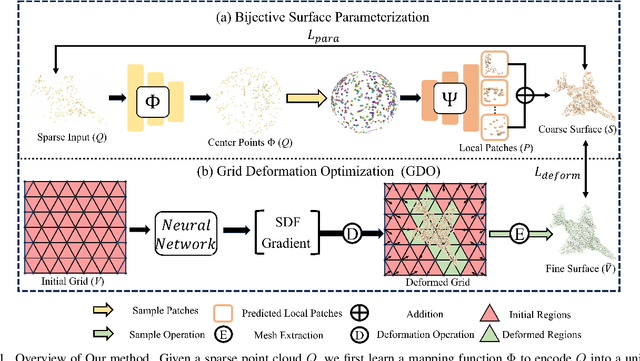
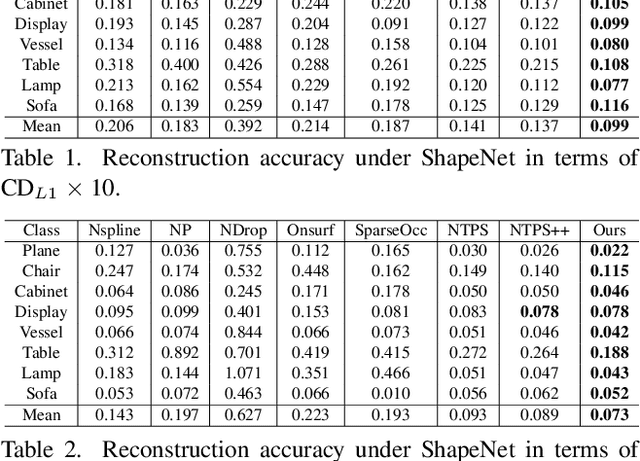
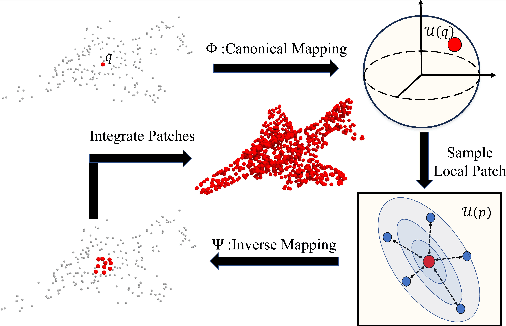
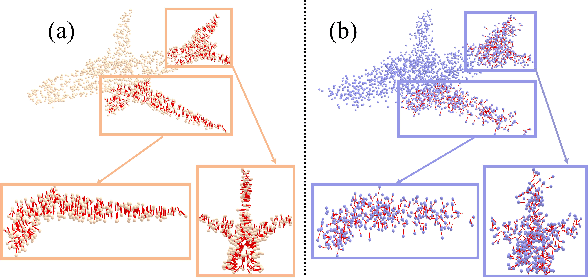
Inferring signed distance functions (SDFs) from sparse point clouds remains a challenge in surface reconstruction. The key lies in the lack of detailed geometric information in sparse point clouds, which is essential for learning a continuous field. To resolve this issue, we present a novel approach that learns a dynamic deformation network to predict SDFs in an end-to-end manner. To parameterize a continuous surface from sparse points, we propose a bijective surface parameterization (BSP) that learns the global shape from local patches. Specifically, we construct a bijective mapping for sparse points from the parametric domain to 3D local patches, integrating patches into the global surface. Meanwhile, we introduce grid deformation optimization (GDO) into the surface approximation to optimize the deformation of grid points and further refine the parametric surfaces. Experimental results on synthetic and real scanned datasets demonstrate that our method significantly outperforms the current state-of-the-art methods. Project page: https://takeshie.github.io/Bijective-SDF

GaussianUDF: Inferring Unsigned Distance Functions through 3D Gaussian Splatting

Reconstructing open surfaces from multi-view images is vital in digitalizing complex objects in daily life. A widely used strategy is to learn unsigned distance functions (UDFs) by checking if their appearance conforms to the image observations through neural rendering. However, it is still hard to learn continuous and implicit UDF representations through 3D Gaussians splatting (3DGS) due to the discrete and explicit scene representation, i.e., 3D Gaussians. To resolve this issue, we propose a novel approach to bridge the gap between 3D Gaussians and UDFs. Our key idea is to overfit thin and flat 2D Gaussian planes on surfaces, and then, leverage the self-supervision and gradient-based inference to supervise unsigned distances in both near and far area to surfaces. To this end, we introduce novel constraints and strategies to constrain the learning of 2D Gaussians to pursue more stable optimization and more reliable self-supervision, addressing the challenges brought by complicated gradient field on or near the zero level set of UDFs. We report numerical and visual comparisons with the state-of-the-art on widely used benchmarks and real data to show our advantages in terms of accuracy, efficiency, completeness, and sharpness of reconstructed open surfaces with boundaries. Project page: https://lisj575.github.io/GaussianUDF/

Sharpening Neural Implicit Functions with Frequency Consolidation Priors

Signed Distance Functions (SDFs) are vital implicit representations to represent high fidelity 3D surfaces. Current methods mainly leverage a neural network to learn an SDF from various supervisions including signed distances, 3D point clouds, or multi-view images. However, due to various reasons including the bias of neural network on low frequency content, 3D unaware sampling, sparsity in point clouds, or low resolutions of images, neural implicit representations still struggle to represent geometries with high frequency components like sharp structures, especially for the ones learned from images or point clouds. To overcome this challenge, we introduce a method to sharpen a low frequency SDF observation by recovering its high frequency components, pursuing a sharper and more complete surface. Our key idea is to learn a mapping from a low frequency observation to a full frequency coverage in a data-driven manner, leading to a prior knowledge of shape consolidation in the frequency domain, dubbed frequency consolidation priors. To better generalize a learned prior to unseen shapes, we introduce to represent frequency components as embeddings and disentangle the embedding of the low frequency component from the embedding of the full frequency component. This disentanglement allows the prior to generalize on an unseen low frequency observation by simply recovering its full frequency embedding through a test-time self-reconstruction. Our evaluations under widely used benchmarks or real scenes show that our method can recover high frequency component and produce more accurate surfaces than the latest methods. The code, data, and pre-trained models are available at \url{https://github.com/chenchao15/FCP}.

Sensing Surface Patches in Volume Rendering for Inferring Signed Distance Functions

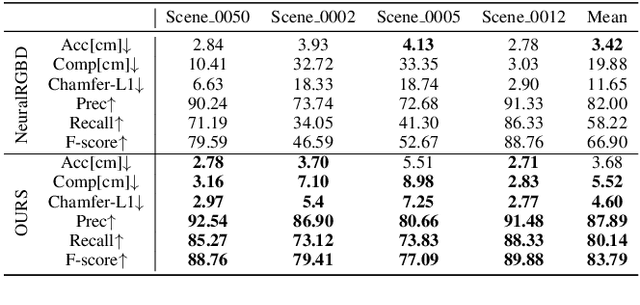
It is vital to recover 3D geometry from multi-view RGB images in many 3D computer vision tasks. The latest methods infer the geometry represented as a signed distance field by minimizing the rendering error on the field through volume rendering. However, it is still challenging to explicitly impose constraints on surfaces for inferring more geometry details due to the limited ability of sensing surfaces in volume rendering. To resolve this problem, we introduce a method to infer signed distance functions (SDFs) with a better sense of surfaces through volume rendering. Using the gradients and signed distances, we establish a small surface patch centered at the estimated intersection along a ray by pulling points randomly sampled nearby. Hence, we are able to explicitly impose surface constraints on the sensed surface patch, such as multi-view photo consistency and supervision from depth or normal priors, through volume rendering. We evaluate our method by numerical and visual comparisons on scene benchmarks. Our superiority over the latest methods justifies our effectiveness.

Query Quantized Neural SLAM

Neural implicit representations have shown remarkable abilities in jointly modeling geometry, color, and camera poses in simultaneous localization and mapping (SLAM). Current methods use coordinates, positional encodings, or other geometry features as input to query neural implicit functions for signed distances and color which produce rendering errors to drive the optimization in overfitting image observations. However, due to the run time efficiency requirement in SLAM systems, we are merely allowed to conduct optimization on each frame in few iterations, which is far from enough for neural networks to overfit these queries. The underfitting usually results in severe drifts in camera tracking and artifacts in reconstruction. To resolve this issue, we propose query quantized neural SLAM which uses quantized queries to reduce variations of input for much easier and faster overfitting a frame. To this end, we quantize a query into a discrete representation with a set of codes, and only allow neural networks to observe a finite number of variations. This allows neural networks to become increasingly familiar with these codes after overfitting more and more previous frames. Moreover, we also introduce novel initialization, losses, and argumentation to stabilize the optimization with significant uncertainty in the early optimization stage, constrain the optimization space, and estimate camera poses more accurately. We justify the effectiveness of each design and report visual and numerical comparisons on widely used benchmarks to show our superiority over the latest methods in both reconstruction and camera tracking.

MultiPull: Detailing Signed Distance Functions by Pulling Multi-Level Queries at Multi-Step

Reconstructing a continuous surface from a raw 3D point cloud is a challenging task. Recent methods usually train neural networks to overfit on single point clouds to infer signed distance functions (SDFs). However, neural networks tend to smooth local details due to the lack of ground truth signed distances or normals, which limits the performance of overfitting-based methods in reconstruction tasks. To resolve this issue, we propose a novel method, named MultiPull, to learn multi-scale implicit fields from raw point clouds by optimizing accurate SDFs from coarse to fine. We achieve this by mapping 3D query points into a set of frequency features, which makes it possible to leverage multi-level features during optimization. Meanwhile, we introduce optimization constraints from the perspective of spatial distance and normal consistency, which play a key role in point cloud reconstruction based on multi-scale optimization strategies. Our experiments on widely used object and scene benchmarks demonstrate that our method outperforms the state-of-the-art methods in surface reconstruction.

Inferring Neural Signed Distance Functions by Overfitting on Single Noisy Point Clouds through Finetuning Data-Driven based Priors

It is important to estimate an accurate signed distance function (SDF) from a point cloud in many computer vision applications. The latest methods learn neural SDFs using either a data-driven based or an overfitting-based strategy. However, these two kinds of methods are with either poor generalization or slow convergence, which limits their capability under challenging scenarios like highly noisy point clouds. To resolve this issue, we propose a method to promote pros of both data-driven based and overfitting-based methods for better generalization, faster inference, and higher accuracy in learning neural SDFs. We introduce a novel statistical reasoning algorithm in local regions which is able to finetune data-driven based priors without signed distance supervision, clean point cloud, or point normals. This helps our method start with a good initialization, and converge to a minimum in a much faster way. Our numerical and visual comparisons with the state-of-the-art methods show our superiority over these methods in surface reconstruction and point cloud denoising on widely used shape and scene benchmarks. The code is available at https://github.com/chenchao15/LocalN2NM.

Binocular-Guided 3D Gaussian Splatting with View Consistency for Sparse View Synthesis

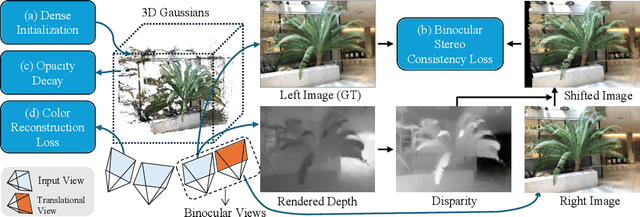
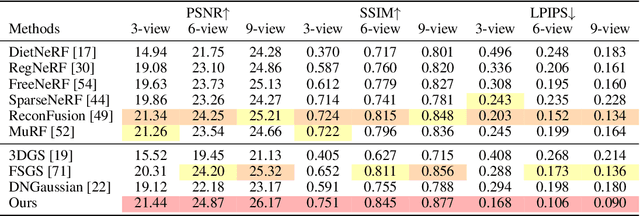
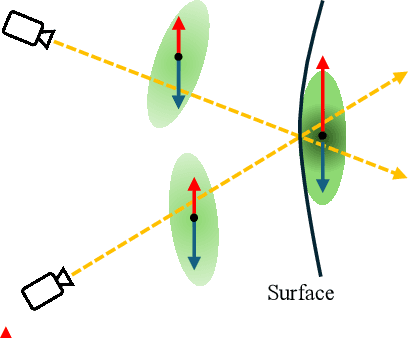
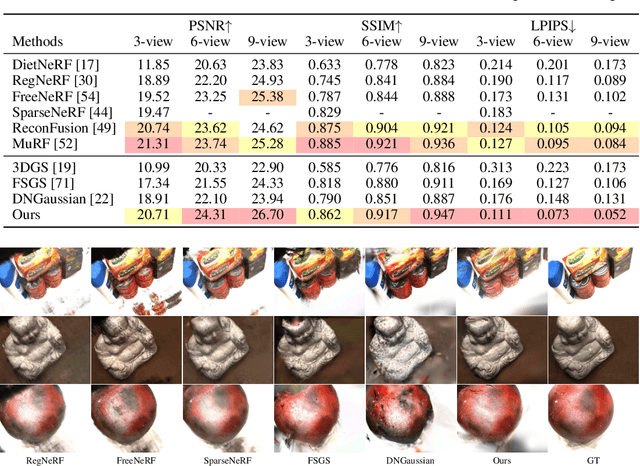
Novel view synthesis from sparse inputs is a vital yet challenging task in 3D computer vision. Previous methods explore 3D Gaussian Splatting with neural priors (e.g. depth priors) as an additional supervision, demonstrating promising quality and efficiency compared to the NeRF based methods. However, the neural priors from 2D pretrained models are often noisy and blurry, which struggle to precisely guide the learning of radiance fields. In this paper, We propose a novel method for synthesizing novel views from sparse views with Gaussian Splatting that does not require external prior as supervision. Our key idea lies in exploring the self-supervisions inherent in the binocular stereo consistency between each pair of binocular images constructed with disparity-guided image warping. To this end, we additionally introduce a Gaussian opacity constraint which regularizes the Gaussian locations and avoids Gaussian redundancy for improving the robustness and efficiency of inferring 3D Gaussians from sparse views. Extensive experiments on the LLFF, DTU, and Blender datasets demonstrate that our method significantly outperforms the state-of-the-art methods.

Zero-Shot Scene Reconstruction from Single Images with Deep Prior Assembly

Large language and vision models have been leading a revolution in visual computing. By greatly scaling up sizes of data and model parameters, the large models learn deep priors which lead to remarkable performance in various tasks. In this work, we present deep prior assembly, a novel framework that assembles diverse deep priors from large models for scene reconstruction from single images in a zero-shot manner. We show that this challenging task can be done without extra knowledge but just simply generalizing one deep prior in one sub-task. To this end, we introduce novel methods related to poses, scales, and occlusion parsing which are keys to enable deep priors to work together in a robust way. Deep prior assembly does not require any 3D or 2D data-driven training in the task and demonstrates superior performance in generalizing priors to open-world scenes. We conduct evaluations on various datasets, and report analysis, numerical and visual comparisons with the latest methods to show our superiority. Project page: https://junshengzhou.github.io/DeepPriorAssembly.

Neural Signed Distance Function Inference through Splatting 3D Gaussians Pulled on Zero-Level Set

It is vital to infer a signed distance function (SDF) in multi-view based surface reconstruction. 3D Gaussian splatting (3DGS) provides a novel perspective for volume rendering, and shows advantages in rendering efficiency and quality. Although 3DGS provides a promising neural rendering option, it is still hard to infer SDFs for surface reconstruction with 3DGS due to the discreteness, the sparseness, and the off-surface drift of 3D Gaussians. To resolve these issues, we propose a method that seamlessly merge 3DGS with the learning of neural SDFs. Our key idea is to more effectively constrain the SDF inference with the multi-view consistency. To this end, we dynamically align 3D Gaussians on the zero-level set of the neural SDF using neural pulling, and then render the aligned 3D Gaussians through the differentiable rasterization. Meanwhile, we update the neural SDF by pulling neighboring space to the pulled 3D Gaussians, which progressively refine the signed distance field near the surface. With both differentiable pulling and splatting, we jointly optimize 3D Gaussians and the neural SDF with both RGB and geometry constraints, which recovers more accurate, smooth, and complete surfaces with more geometry details. Our numerical and visual comparisons show our superiority over the state-of-the-art results on the widely used benchmarks.