Fast Track to Winning Tickets: Repowering One-Shot Pruning for Graph Neural Networks

Graph Neural Networks (GNNs) demonstrate superior performance in various graph learning tasks, yet their wider real-world application is hindered by the computational overhead when applied to large-scale graphs. To address the issue, the Graph Lottery Hypothesis (GLT) has been proposed, advocating the identification of subgraphs and subnetworks, \textit{i.e.}, winning tickets, without compromising performance. The effectiveness of current GLT methods largely stems from the use of iterative magnitude pruning (IMP), which offers higher stability and better performance than one-shot pruning. However, identifying GLTs is highly computationally expensive, due to the iterative pruning and retraining required by IMP. In this paper, we reevaluate the correlation between one-shot pruning and IMP: while one-shot tickets are suboptimal compared to IMP, they offer a \textit{fast track} to tickets with a stronger performance. We introduce a one-shot pruning and denoising framework to validate the efficacy of the \textit{fast track}. Compared to current IMP-based GLT methods, our framework achieves a double-win situation of graph lottery tickets with \textbf{higher sparsity} and \textbf{faster speeds}. Through extensive experiments across 4 backbones and 6 datasets, our method demonstrates $1.32\% - 45.62\%$ improvement in weight sparsity and a $7.49\% - 22.71\%$ increase in graph sparsity, along with a $1.7-44 \times$ speedup over IMP-based methods and $95.3\%-98.6\%$ MAC savings.

G-Designer: Architecting Multi-agent Communication Topologies via Graph Neural Networks

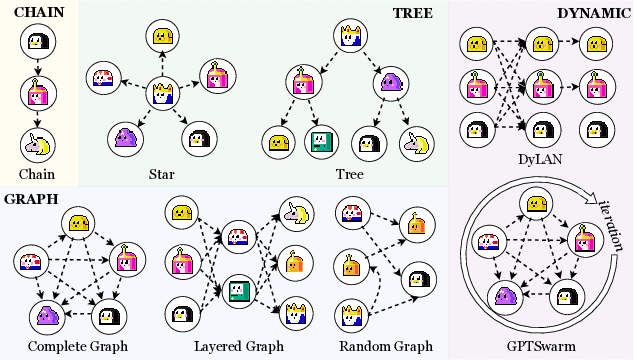
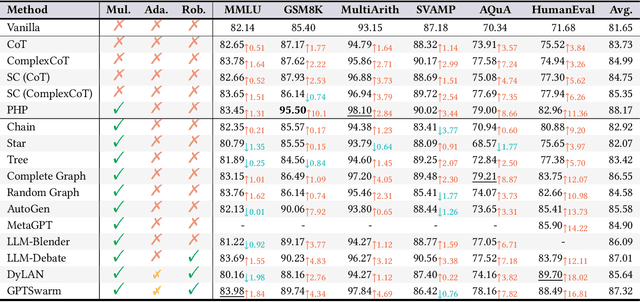
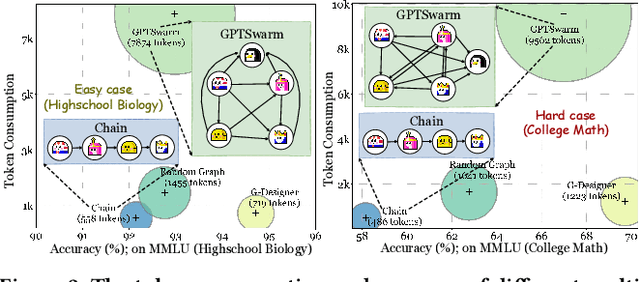
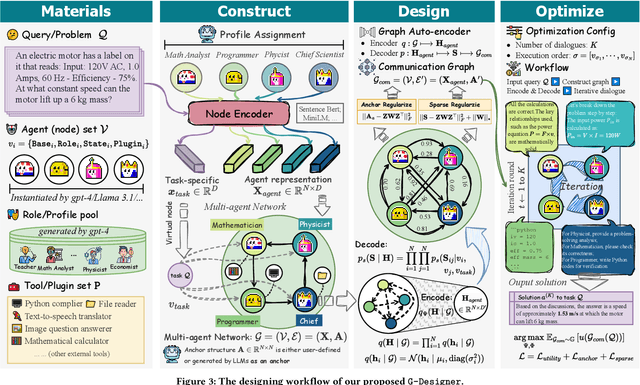
Recent advancements in large language model (LLM)-based agents have demonstrated that collective intelligence can significantly surpass the capabilities of individual agents, primarily due to well-crafted inter-agent communication topologies. Despite the diverse and high-performing designs available, practitioners often face confusion when selecting the most effective pipeline for their specific task: \textit{Which topology is the best choice for my task, avoiding unnecessary communication token overhead while ensuring high-quality solution?} In response to this dilemma, we introduce G-Designer, an adaptive, efficient, and robust solution for multi-agent deployment, which dynamically designs task-aware, customized communication topologies. Specifically, G-Designer models the multi-agent system as a multi-agent network, leveraging a variational graph auto-encoder to encode both the nodes (agents) and a task-specific virtual node, and decodes a task-adaptive and high-performing communication topology. Extensive experiments on six benchmarks showcase that G-Designer is: \textbf{(1) high-performing}, achieving superior results on MMLU with accuracy at $84.50\%$ and on HumanEval with pass@1 at $89.90\%$; \textbf{(2) task-adaptive}, architecting communication protocols tailored to task difficulty, reducing token consumption by up to $95.33\%$ on HumanEval; and \textbf{(3) adversarially robust}, defending against agent adversarial attacks with merely $0.3\%$ accuracy drop.

Cut the Crap: An Economical Communication Pipeline for LLM-based Multi-Agent Systems

Recent advancements in large language model (LLM)-powered agents have shown that collective intelligence can significantly outperform individual capabilities, largely attributed to the meticulously designed inter-agent communication topologies. Though impressive in performance, existing multi-agent pipelines inherently introduce substantial token overhead, as well as increased economic costs, which pose challenges for their large-scale deployments. In response to this challenge, we propose an economical, simple, and robust multi-agent communication framework, termed $\texttt{AgentPrune}$, which can seamlessly integrate into mainstream multi-agent systems and prunes redundant or even malicious communication messages. Technically, $\texttt{AgentPrune}$ is the first to identify and formally define the \textit{communication redundancy} issue present in current LLM-based multi-agent pipelines, and efficiently performs one-shot pruning on the spatial-temporal message-passing graph, yielding a token-economic and high-performing communication topology. Extensive experiments across six benchmarks demonstrate that $\texttt{AgentPrune}$ \textbf{(I)} achieves comparable results as state-of-the-art topologies at merely $\$5.6$ cost compared to their $\$43.7$, \textbf{(II)} integrates seamlessly into existing multi-agent frameworks with $28.1\%\sim72.8\%\downarrow$ token reduction, and \textbf{(III)} successfully defend against two types of agent-based adversarial attacks with $3.5\%\sim10.8\%\uparrow$ performance boost.

Graph Sparsification via Mixture of Graphs

Graph Neural Networks (GNNs) have demonstrated superior performance across various graph learning tasks but face significant computational challenges when applied to large-scale graphs. One effective approach to mitigate these challenges is graph sparsification, which involves removing non-essential edges to reduce computational overhead. However, previous graph sparsification methods often rely on a single global sparsity setting and uniform pruning criteria, failing to provide customized sparsification schemes for each node's complex local context. In this paper, we introduce Mixture-of-Graphs (MoG), leveraging the concept of Mixture-of-Experts (MoE), to dynamically select tailored pruning solutions for each node. Specifically, MoG incorporates multiple sparsifier experts, each characterized by unique sparsity levels and pruning criteria, and selects the appropriate experts for each node. Subsequently, MoG performs a mixture of the sparse graphs produced by different experts on the Grassmann manifold to derive an optimal sparse graph. One notable property of MoG is its entirely local nature, as it depends on the specific circumstances of each individual node. Extensive experiments on four large-scale OGB datasets and two superpixel datasets, equipped with five GNN backbones, demonstrate that MoG (I) identifies subgraphs at higher sparsity levels ($8.67\%\sim 50.85\%$), with performance equal to or better than the dense graph, (II) achieves $1.47-2.62\times$ speedup in GNN inference with negligible performance drop, and (III) boosts ``top-student'' GNN performance ($1.02\%\uparrow$ on RevGNN+\textsc{ogbn-proteins} and $1.74\%\uparrow$ on DeeperGCN+\textsc{ogbg-ppa}).

Two Heads Are Better Than One: Boosting Graph Sparse Training via Semantic and Topological Awareness

Graph Neural Networks (GNNs) excel in various graph learning tasks but face computational challenges when applied to large-scale graphs. A promising solution is to remove non-essential edges to reduce the computational overheads in GNN. Previous literature generally falls into two categories: topology-guided and semantic-guided. The former maintains certain graph topological properties yet often underperforms on GNNs due to low integration with neural network training. The latter performs well at lower sparsity on GNNs but faces performance collapse at higher sparsity levels. With this in mind, we take the first step to propose a new research line and concept termed Graph Sparse Training (GST), which dynamically manipulates sparsity at the data level. Specifically, GST initially constructs a topology & semantic anchor at a low training cost, followed by performing dynamic sparse training to align the sparse graph with the anchor. We introduce the Equilibria Sparsification Principle to guide this process, effectively balancing the preservation of both topological and semantic information. Ultimately, GST produces a sparse graph with maximum topological integrity and no performance degradation. Extensive experiments on 6 datasets and 5 backbones showcase that GST (I) identifies subgraphs at higher graph sparsity levels (1.67%~15.85% $\uparrow$) than state-of-the-art sparsification methods, (II) preserves more key spectral properties, (III) achieves 1.27-3.42$\times$ speedup in GNN inference and (IV) successfully helps graph adversarial defense and graph lottery tickets.