OCRVerse: Towards Holistic OCR in End-to-End Vision-Language Models

The development of large vision language models drives the demand for managing, and applying massive amounts of multimodal data, making OCR technology, which extracts information from visual images, increasingly popular. However, existing OCR methods primarily focus on recognizing text elements from images or scanned documents (\textbf{Text-centric OCR}), neglecting the identification of visual elements from visually information-dense image sources (\textbf{Vision-centric OCR}), such as charts, web pages and science plots. In reality, these visually information-dense images are widespread on the internet and have significant real-world application value, such as data visualization and web page analysis. In this technical report, we propose \textbf{OCRVerse}, the first holistic OCR method in end-to-end manner that enables unified text-centric OCR and vision-centric OCR. To this end, we constructe comprehensive data engineering to cover a wide range of text-centric documents, such as newspapers, magazines and books, as well as vision-centric rendered composites, including charts, web pages and scientific plots. Moreover, we propose a two-stage SFT-RL multi-domain training method for OCRVerse. SFT directly mixes cross-domain data to train and establish initial domain knowledge, while RL focuses on designing personalized reward strategies for the characteristics of each domain. Specifically, since different domains require various output formats and expected outputs, we provide sufficient flexibility in the RL stage to customize flexible reward signals for each domain, thereby improving cross-domain fusion and avoiding data conflicts. Experimental results demonstrate the effectiveness of OCRVerse, achieving competitive results across text-centric and vision-centric data types, even comparable to large-scale open-source and closed-source models.

TinyChemVL: Advancing Chemical Vision-Language Models via Efficient Visual Token Reduction and Complex Reaction Tasks

While Vision Language Models (VLMs) have demonstrated remarkable capabilities in general visual understanding, their application in the chemical domain has been limited, with previous works predominantly focusing on text and thus overlooking critical visual information, such as molecular structures. Current approaches that directly adopt standard VLMs for chemical tasks suffer from two primary issues: (i) computational inefficiency of processing entire chemical images with non-informative backgrounds. (ii) a narrow scope on molecular-level tasks that restricts progress in chemical reasoning. In this work, we propose \textbf{TinyChemVL}, an efficient and powerful chemical VLM that leverages visual token reduction and reaction-level tasks to improve model efficiency and reasoning capacity. Also, we propose \textbf{ChemRxn-V}, a reaction-level benchmark for assessing vision-based reaction recognition and prediction tasks. Directly predicting reaction products from molecular images poses a non-trivial challenge, as it requires models to integrate both recognition and reasoning capacities. Our results demonstrate that with only 4B parameters, TinyChemVL achieves superior performance on both molecular and reaction tasks while demonstrating faster inference and training speeds compared to existing models. Notably, TinyChemVL outperforms ChemVLM while utilizing only 1/16th of the visual tokens. This work builds efficient yet powerful VLMs for chemical domains by co-designing model architecture and task complexity.

Automating Hardware Design and Verification from Architectural Papers via a Neural-Symbolic Graph Framework

The reproduction of hardware architectures from academic papers remains a significant challenge due to the lack of publicly available source code and the complexity of hardware description languages (HDLs). To this end, we propose \textbf{ArchCraft}, a Framework that converts abstract architectural descriptions from academic papers into synthesizable Verilog projects with register-transfer level (RTL) verification. ArchCraft introduces a structured workflow, which uses formal graphs to capture the Architectural Blueprint and symbols to define the Functional Specification, translating unstructured academic papers into verifiable, hardware-aware designs. The framework then generates RTL and testbench (TB) code decoupled via these symbols to facilitate verification and debugging, ultimately reporting the circuit's Power, Area, and Performance (PPA). Moreover, we propose the first benchmark, \textbf{ArchSynthBench}, for synthesizing hardware from architectural descriptions, with a complete set of evaluation indicators, 50 project-level circuits, and around 600 circuit blocks. We systematically assess ArchCraft on ArchSynthBench, where the experiment results demonstrate the superiority of our proposed method, surpassing direct generation methods and the VerilogCoder framework in both paper understanding and code completion. Furthermore, evaluation and physical implementation of the generated executable RTL code show that these implementations meet all timing constraints without violations, and their performance metrics are consistent with those reported in the original papers.

AutoReproduce: Automatic AI Experiment Reproduction with Paper Lineage

Efficient experiment reproduction is critical to accelerating progress in artificial intelligence. However, the inherent complexity of method design and training procedures presents substantial challenges for automation. Notably, reproducing experiments often requires implicit domain-specific knowledge not explicitly documented in the original papers. To address this, we introduce the paper lineage algorithm, which identifies and extracts implicit knowledge from the relevant references cited by the target paper. Building on this idea, we propose AutoReproduce, a multi-agent framework capable of automatically reproducing experiments described in research papers in an end-to-end manner. AutoReproduce enhances code executability by generating unit tests alongside the reproduction process. To evaluate the reproduction capability, we construct ReproduceBench, a benchmark annotated with verified implementations, and introduce novel evaluation metrics to assess both the reproduction and execution fidelity. Experimental results demonstrate that AutoReproduce outperforms the existing strong agent baselines on all five evaluation metrics by a peak margin of over $70\%$. In particular, compared to the official implementations, AutoReproduce achieves an average performance gap of $22.1\%$ on $89.74\%$ of the executable experiment runs. The code will be available at https://github.com/AI9Stars/AutoReproduce.

ChartEdit: How Far Are MLLMs From Automating Chart Analysis? Evaluating MLLMs' Capability via Chart Editing

Although multimodal large language models (MLLMs) show promise in generating chart rendering code, chart editing presents a greater challenge. This difficulty stems from its nature as a labor-intensive task for humans that also demands MLLMs to integrate chart understanding, complex reasoning, and precise intent interpretation. While many MLLMs claim such editing capabilities, current assessments typically rely on limited case studies rather than robust evaluation methodologies, highlighting the urgent need for a comprehensive evaluation framework. In this work, we propose ChartEdit, a new high-quality benchmark designed for chart editing tasks. This benchmark comprises $1,405$ diverse editing instructions applied to $233$ real-world charts, with each instruction-chart instance having been manually annotated and validated for accuracy. Utilizing ChartEdit, we evaluate the performance of 10 mainstream MLLMs across two types of experiments, assessing them at both the code and chart levels. The results suggest that large-scale models can generate code to produce images that partially match the reference images. However, their ability to generate accurate edits according to the instructions remains limited. The state-of-the-art (SOTA) model achieves a score of only $59.96$, highlighting significant challenges in precise modification. In contrast, small-scale models, including chart-domain models, struggle both with following editing instructions and generating overall chart images, underscoring the need for further development in this area. Code is available at https://github.com/xxlllz/ChartEdit.

ChartCoder: Advancing Multimodal Large Language Model for Chart-to-Code Generation

Multimodal Large Language Models (MLLMs) have demonstrated remarkable capabilities in chart understanding tasks. However, interpreting charts with textual descriptions often leads to information loss, as it fails to fully capture the dense information embedded in charts. In contrast, parsing charts into code provides lossless representations that can effectively contain all critical details. Although existing open-source MLLMs have achieved success in chart understanding tasks, they still face two major challenges when applied to chart-to-code tasks.: (1) Low executability and poor restoration of chart details in the generated code and (2) Lack of large-scale and diverse training data. To address these challenges, we propose \textbf{ChartCoder}, the first dedicated chart-to-code MLLM, which leverages Code LLMs as the language backbone to enhance the executability of the generated code. Furthermore, we introduce \textbf{Chart2Code-160k}, the first large-scale and diverse dataset for chart-to-code generation, and propose the \textbf{Snippet-of-Thought (SoT)} method, which transforms direct chart-to-code generation data into step-by-step generation. Experiments demonstrate that ChartCoder, with only 7B parameters, surpasses existing open-source MLLMs on chart-to-code benchmarks, achieving superior chart restoration and code excitability. Our code will be available at https://github.com/thunlp/ChartCoder.

Enhanced Spatiotemporal Prediction Using Physical-guided And Frequency-enhanced Recurrent Neural Networks

Spatiotemporal prediction plays an important role in solving natural problems and processing video frames, especially in weather forecasting and human action recognition. Recent advances attempt to incorporate prior physical knowledge into the deep learning framework to estimate the unknown governing partial differential equations (PDEs), which have shown promising results in spatiotemporal prediction tasks. However, previous approaches only restrict neural network architectures or loss functions to acquire physical or PDE features, which decreases the representative capacity of a neural network. Meanwhile, the updating process of the physical state cannot be effectively estimated. To solve the above mentioned problems, this paper proposes a physical-guided neural network, which utilizes the frequency-enhanced Fourier module and moment loss to strengthen the model's ability to estimate the spatiotemporal dynamics. Furthermore, we propose an adaptive second-order Runge-Kutta method with physical constraints to model the physical states more precisely. We evaluate our model on both spatiotemporal and video prediction tasks. The experimental results show that our model outperforms state-of-the-art methods and performs best in several datasets, with a much smaller parameter count.

Local Convolution Enhanced Global Fourier Neural Operator For Multiscale Dynamic Spaces Prediction

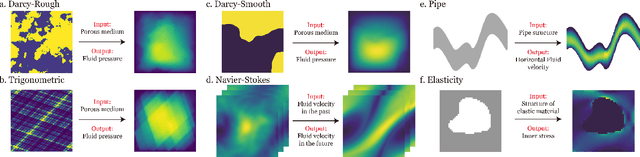
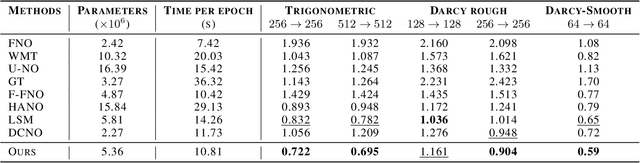
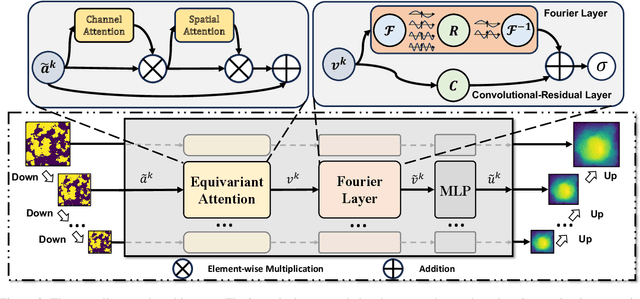
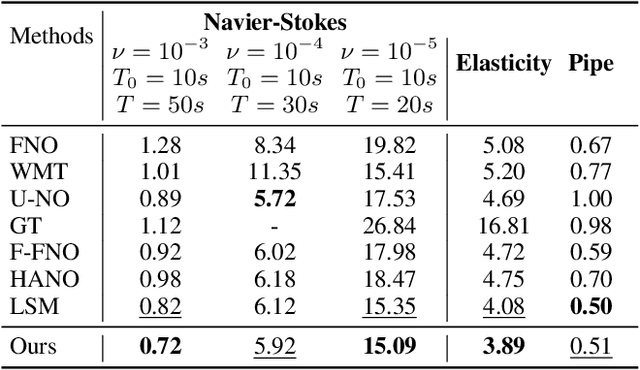
Neural operators extend the capabilities of traditional neural networks by allowing them to handle mappings between function spaces for the purpose of solving partial differential equations (PDEs). One of the most notable methods is the Fourier Neural Operator (FNO), which is inspired by Green's function method and approximate operator kernel directly in the frequency domain. In this work, we focus on predicting multiscale dynamic spaces, which is equivalent to solving multiscale PDEs. Multiscale PDEs are characterized by rapid coefficient changes and solution space oscillations, which are crucial for modeling atmospheric convection and ocean circulation. To solve this problem, models should have the ability to capture rapid changes and process them at various scales. However, the FNO only approximates kernels in the low-frequency domain, which is insufficient when solving multiscale PDEs. To address this challenge, we propose a novel hierarchical neural operator that integrates improved Fourier layers with attention mechanisms, aiming to capture all details and handle them at various scales. These mechanisms complement each other in the frequency domain and encourage the model to solve multiscale problems. We perform experiments on dynamic spaces governed by forward and reverse problems of multiscale elliptic equations, Navier-Stokes equations and some other physical scenarios, and reach superior performance in existing PDE benchmarks, especially equations characterized by rapid coefficient variations.

ODE-based Recurrent Model-free Reinforcement Learning for POMDPs

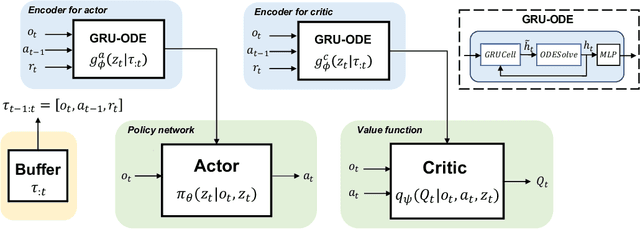
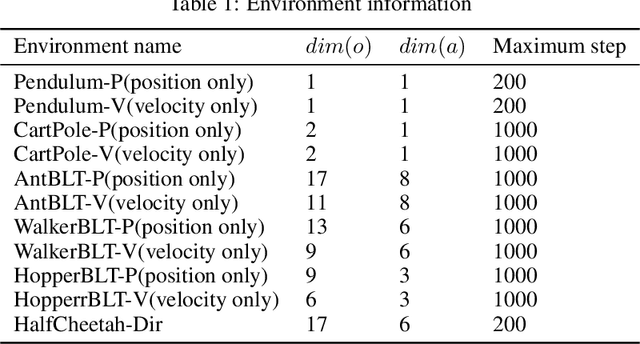
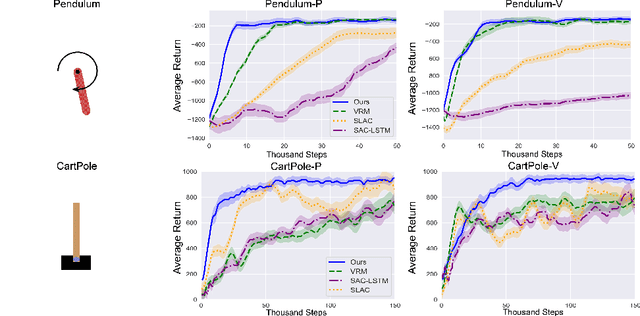
Neural ordinary differential equations (ODEs) are widely recognized as the standard for modeling physical mechanisms, which help to perform approximate inference in unknown physical or biological environments. In partially observable (PO) environments, how to infer unseen information from raw observations puzzled the agents. By using a recurrent policy with a compact context, context-based reinforcement learning provides a flexible way to extract unobservable information from historical transitions. To help the agent extract more dynamics-related information, we present a novel ODE-based recurrent model combines with model-free reinforcement learning (RL) framework to solve partially observable Markov decision processes (POMDPs). We experimentally demonstrate the efficacy of our methods across various PO continuous control and meta-RL tasks. Furthermore, our experiments illustrate that our method is robust against irregular observations, owing to the ability of ODEs to model irregularly-sampled time series.