ODE-based Recurrent Model-free Reinforcement Learning for POMDPs
Paper and Code
Sep 25, 2023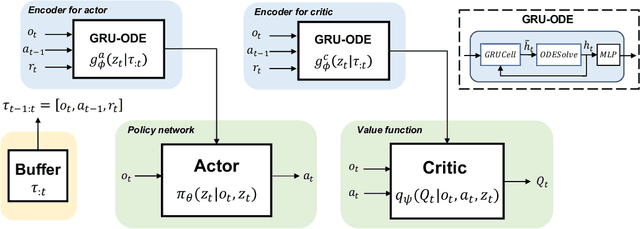
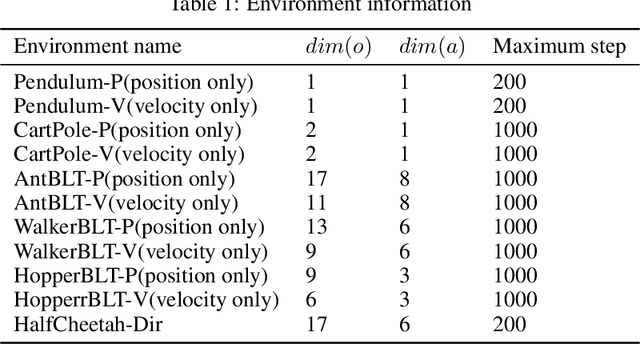
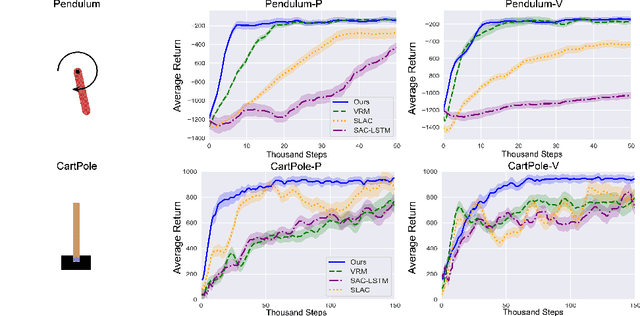
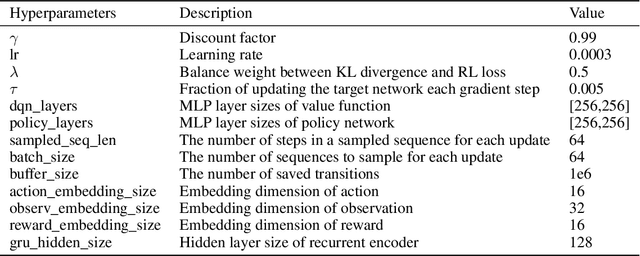
Neural ordinary differential equations (ODEs) are widely recognized as the standard for modeling physical mechanisms, which help to perform approximate inference in unknown physical or biological environments. In partially observable (PO) environments, how to infer unseen information from raw observations puzzled the agents. By using a recurrent policy with a compact context, context-based reinforcement learning provides a flexible way to extract unobservable information from historical transitions. To help the agent extract more dynamics-related information, we present a novel ODE-based recurrent model combines with model-free reinforcement learning (RL) framework to solve partially observable Markov decision processes (POMDPs). We experimentally demonstrate the efficacy of our methods across various PO continuous control and meta-RL tasks. Furthermore, our experiments illustrate that our method is robust against irregular observations, owing to the ability of ODEs to model irregularly-sampled time series.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge