Local Convolution Enhanced Global Fourier Neural Operator For Multiscale Dynamic Spaces Prediction
Paper and Code
Nov 21, 2023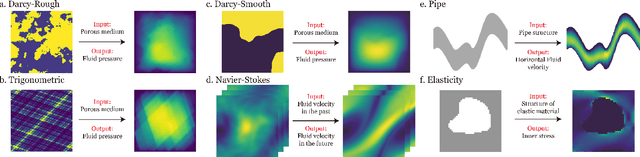
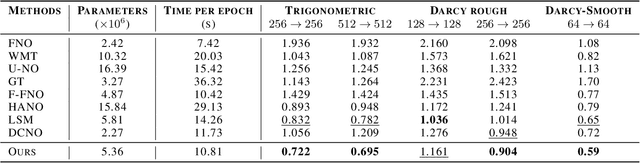
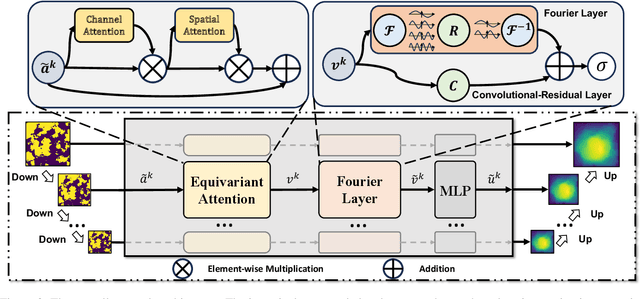
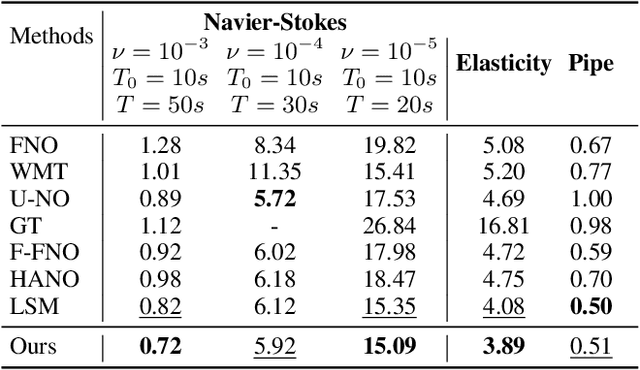
Neural operators extend the capabilities of traditional neural networks by allowing them to handle mappings between function spaces for the purpose of solving partial differential equations (PDEs). One of the most notable methods is the Fourier Neural Operator (FNO), which is inspired by Green's function method and approximate operator kernel directly in the frequency domain. In this work, we focus on predicting multiscale dynamic spaces, which is equivalent to solving multiscale PDEs. Multiscale PDEs are characterized by rapid coefficient changes and solution space oscillations, which are crucial for modeling atmospheric convection and ocean circulation. To solve this problem, models should have the ability to capture rapid changes and process them at various scales. However, the FNO only approximates kernels in the low-frequency domain, which is insufficient when solving multiscale PDEs. To address this challenge, we propose a novel hierarchical neural operator that integrates improved Fourier layers with attention mechanisms, aiming to capture all details and handle them at various scales. These mechanisms complement each other in the frequency domain and encourage the model to solve multiscale problems. We perform experiments on dynamic spaces governed by forward and reverse problems of multiscale elliptic equations, Navier-Stokes equations and some other physical scenarios, and reach superior performance in existing PDE benchmarks, especially equations characterized by rapid coefficient variations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge