Lower Bounds for Time-Varying Kernelized Bandits

The optimization of black-box functions with noisy observations is a fundamental problem with widespread applications, and has been widely studied under the assumption that the function lies in a reproducing kernel Hilbert space (RKHS). This problem has been studied extensively in the stationary setting, and near-optimal regret bounds are known via developments in both upper and lower bounds. In this paper, we consider non-stationary scenarios, which are crucial for certain applications but are currently less well-understood. Specifically, we provide the first algorithm-independent lower bounds, where the time variations are subject satisfying a total variation budget according to some function norm. Under $\ell_{\infty}$-norm variations, our bounds are found to be close to the state-of-the-art upper bound (Hong \emph{et al.}, 2023). Under RKHS norm variations, the upper and lower bounds are still reasonably close but with more of a gap, raising the interesting open question of whether non-minor improvements in the upper bound are possible.

Kernelized Normalizing Constant Estimation: Bridging Bayesian Quadrature and Bayesian Optimization

In this paper, we study the problem of estimating the normalizing constant $\int e^{-\lambda f(x)}dx$ through queries to the black-box function $f$, where $f$ belongs to a reproducing kernel Hilbert space (RKHS), and $\lambda$ is a problem parameter. We show that to estimate the normalizing constant within a small relative error, the level of difficulty depends on the value of $\lambda$: When $\lambda$ approaches zero, the problem is similar to Bayesian quadrature (BQ), while when $\lambda$ approaches infinity, the problem is similar to Bayesian optimization (BO). More generally, the problem varies between BQ and BO. We find that this pattern holds true even when the function evaluations are noisy, bringing new aspects to this topic. Our findings are supported by both algorithm-independent lower bounds and algorithmic upper bounds, as well as simulation studies conducted on a variety of benchmark functions.

Order-Optimal Error Bounds for Noisy Kernel-Based Bayesian Quadrature

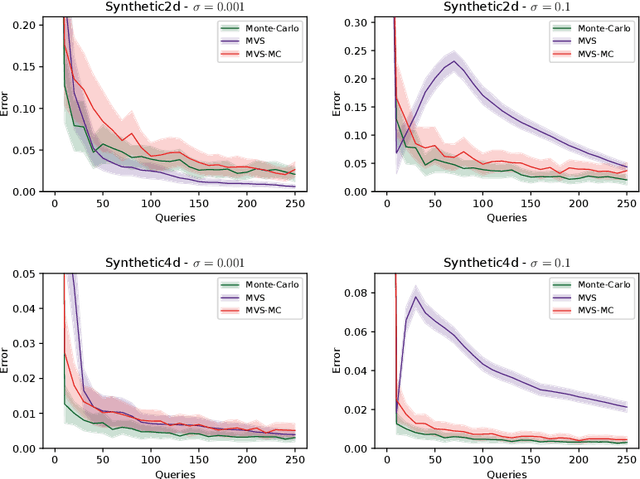
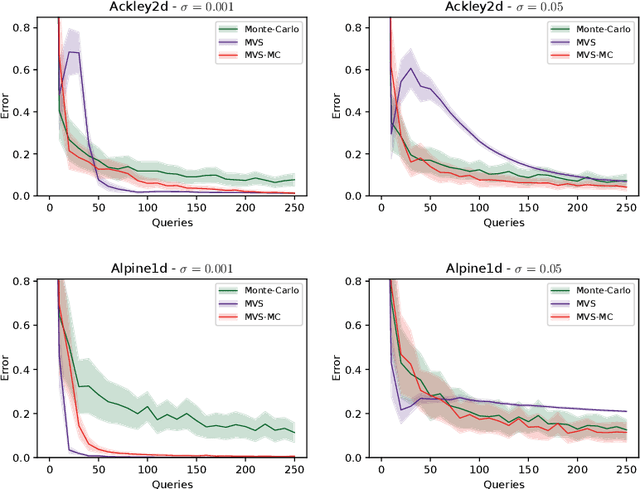
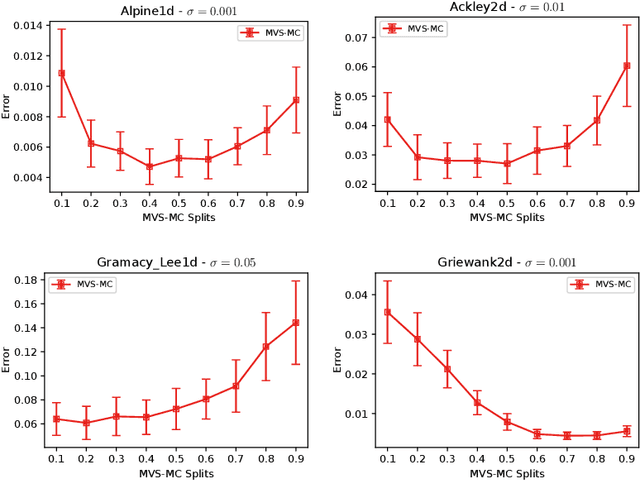
In this paper, we study the sample complexity of {\em noisy Bayesian quadrature} (BQ), in which we seek to approximate an integral based on noisy black-box queries to the underlying function. We consider functions in a {\em Reproducing Kernel Hilbert Space} (RKHS) with the Mat\'ern-$\nu$ kernel, focusing on combinations of the parameter $\nu$ and dimension $d$ such that the RKHS is equivalent to a Sobolev class. In this setting, we provide near-matching upper and lower bounds on the best possible average error. Specifically, we find that when the black-box queries are subject to Gaussian noise having variance $\sigma^2$, any algorithm making at most $T$ queries (even with adaptive sampling) must incur a mean absolute error of $\Omega(T^{-\frac{\nu}{d}-1} + \sigma T^{-\frac{1}{2}})$, and there exists a non-adaptive algorithm attaining an error of at most $O(T^{-\frac{\nu}{d}-1} + \sigma T^{-\frac{1}{2}})$. Hence, the bounds are order-optimal, and establish that there is no adaptivity gap in terms of scaling laws.

Lenient Regret and Good-Action Identification in Gaussian Process Bandits

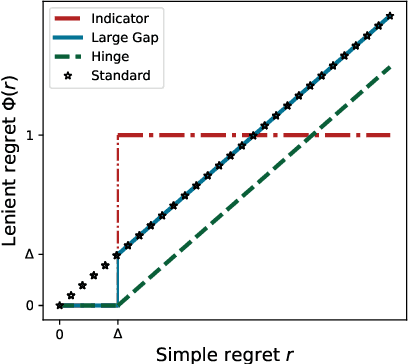
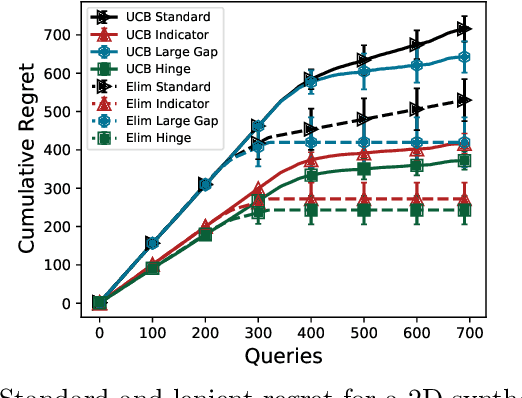
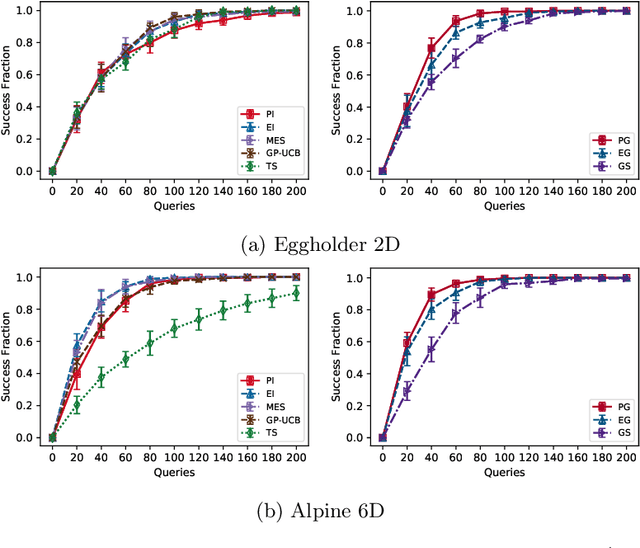
In this paper, we study the problem of Gaussian process (GP) bandits under relaxed optimization criteria stating that any function value above a certain threshold is "good enough". On the theoretical side, we study various \emph{\lenient regret} notions in which all near-optimal actions incur zero penalty, and provide upper bounds on the lenient regret for GP-UCB and an elimination algorithm, circumventing the usual $O(\sqrt{T})$ term (with time horizon $T$) resulting from zooming extremely close towards the function maximum. In addition, we complement these upper bounds with algorithm-independent lower bounds. On the practical side, we consider the problem of finding a single "good action" according to a known pre-specified threshold, and introduce several good-action identification algorithms that exploit knowledge of the threshold. We experimentally find that such algorithms can often find a good action faster than standard optimization-based approaches.

On Lower Bounds for Standard and Robust Gaussian Process Bandit Optimization

In this paper, we consider algorithm-independent lower bounds for the problem of black-box optimization of functions having a bounded norm is some Reproducing Kernel Hilbert Space (RKHS), which can be viewed as a non-Bayesian Gaussian process bandit problem. In the standard noisy setting, we provide a novel proof technique for deriving lower bounds on the regret, with benefits including simplicity, versatility, and an improved dependence on the error probability. In a robust setting in which every sampled point may be perturbed by a suitably-constrained adversary, we provide a novel lower bound for deterministic strategies, demonstrating an inevitable joint dependence of the cumulative regret on the corruption level and the time horizon, in contrast with existing lower bounds that only characterize the individual dependencies. Furthermore, in a distinct robust setting in which the final point is perturbed by an adversary, we strengthen an existing lower bound that only holds for target success probabilities very close to one, by allowing for arbitrary success probabilities in $(0,1)$.

Generalizing Energy-based Generative ConvNets from Particle Evolution Perspective

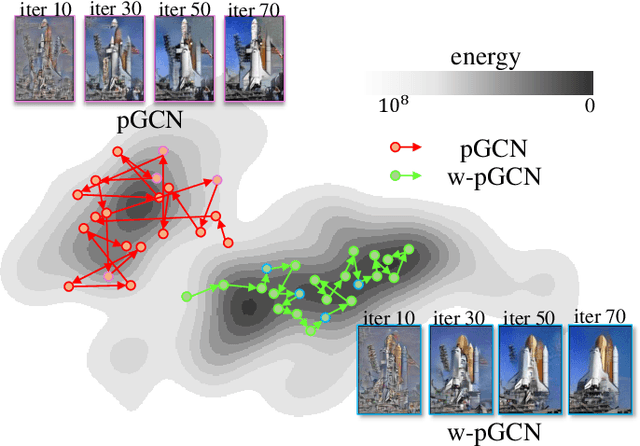
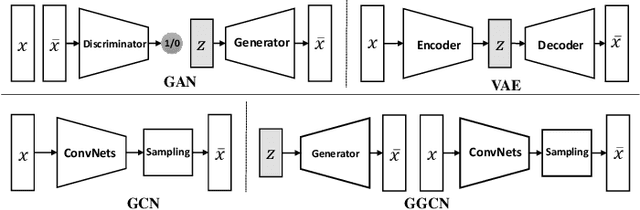
Compared with Generative Adversarial Networks (GAN), the Energy-Based generative Model (EBM) possesses two appealing properties: i) it can be directly optimized without requiring an auxiliary network during the learning and synthesizing; ii) it can better approximate underlying distribution of the observed data by learning explicitly potential functions. This paper studies a branch of EBMs, i.e., the energy-based Generative ConvNet (GCN), which minimizes its energy function defined by a bottom-up ConvNet. From the perspective of particle physics, we solve the problem of unstable energy dissipation that might damage the quality of the synthesized samples during the maximum likelihood learning. Specifically, we establish a connection between FRAME model [1] and dynamic physics process and provide a generalized formulation of FRAME in discrete flow with a certain metric measure from particle perspective. To address KL-vanishing issue, we generalize the reformulated GCN from the KL discrete flow with KL divergence measure to a Jordan-Kinderleher-Otto (JKO) discrete flow with Wasserastein distance metric and derive a Wasserastein GCN (w-GCN). To further minimize the learning bias and improve the model generalization, we present a Generalized GCN (GGCN). GGCN introduces a hidden space mapping strategy and employs a normal distribution as hidden space for the reference distribution. Besides, it applies a matching trainable non-linear upsampling function for further generalization. Considering the limitation of the efficiency problem in MCMC based learning of EBMs, an amortized learning are also proposed to improve the learning efficiency. Quantitative and qualitative experiments are conducted on several widely-used face and natural image datasets. Our experimental results surpass those of the existing models in both model stability and the quality of generated samples.

FRAME Revisited: An Interpretation View Based on Particle Evolution

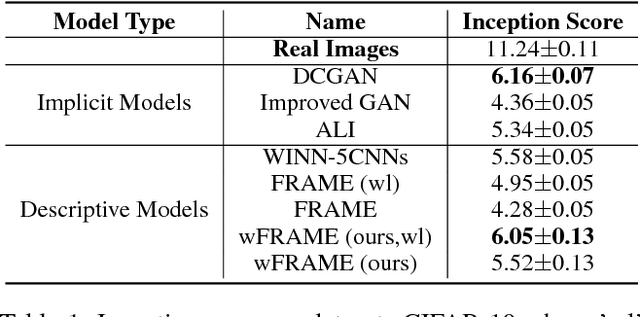
FRAME (Filters, Random fields, And Maximum Entropy) is an energy-based descriptive model that synthesizes visual realism by capturing mutual patterns from structural input signals. The maximum likelihood estimation (MLE) is applied by default, yet conventionally causes the unstable training energy that wrecks the generated structures, which remains unexplained. In this paper, we provide a new theoretical insight to analyze FRAME, from a perspective of particle physics ascribing the weird phenomenon to KL-vanishing issue. In order to stabilize the energy dissipation, we propose an alternative Wasserstein distance in discrete time based on the conclusion that the Jordan-Kinderlehrer-Otto (JKO) discrete flow approximates KL discrete flow when the time step size tends to 0. Besides, this metric can still maintain the model's statistical consistency. Quantitative and qualitative experiments have been respectively conducted on several widely used datasets. The empirical studies have evidenced the effectiveness and superiority of our method.