Order-Optimal Error Bounds for Noisy Kernel-Based Bayesian Quadrature
Paper and Code
Feb 22, 2022
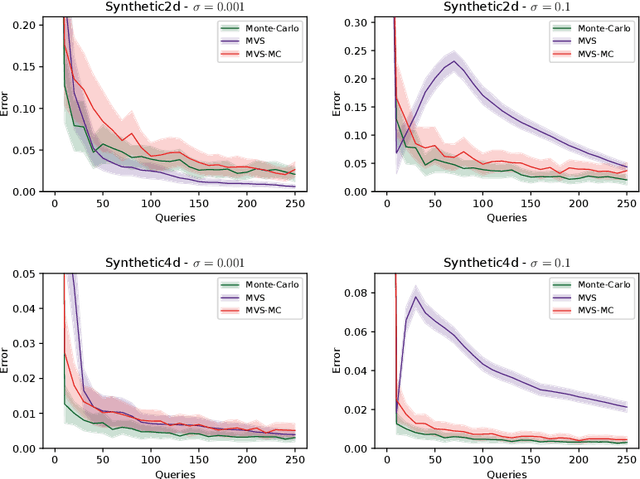
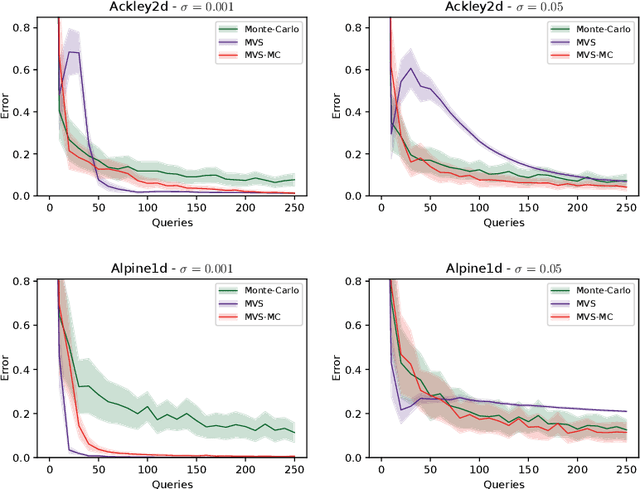
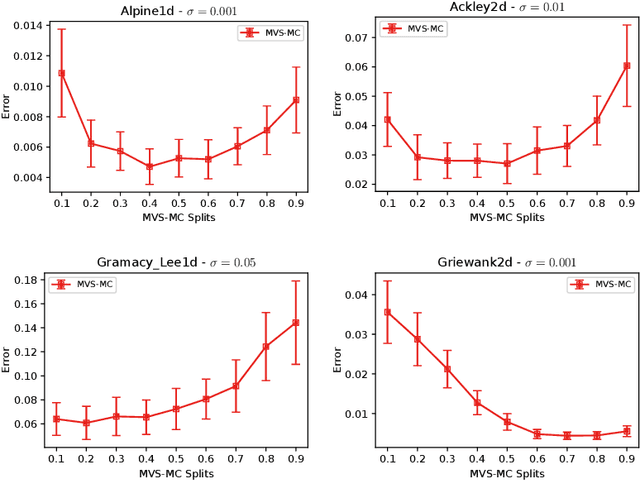
In this paper, we study the sample complexity of {\em noisy Bayesian quadrature} (BQ), in which we seek to approximate an integral based on noisy black-box queries to the underlying function. We consider functions in a {\em Reproducing Kernel Hilbert Space} (RKHS) with the Mat\'ern-$\nu$ kernel, focusing on combinations of the parameter $\nu$ and dimension $d$ such that the RKHS is equivalent to a Sobolev class. In this setting, we provide near-matching upper and lower bounds on the best possible average error. Specifically, we find that when the black-box queries are subject to Gaussian noise having variance $\sigma^2$, any algorithm making at most $T$ queries (even with adaptive sampling) must incur a mean absolute error of $\Omega(T^{-\frac{\nu}{d}-1} + \sigma T^{-\frac{1}{2}})$, and there exists a non-adaptive algorithm attaining an error of at most $O(T^{-\frac{\nu}{d}-1} + \sigma T^{-\frac{1}{2}})$. Hence, the bounds are order-optimal, and establish that there is no adaptivity gap in terms of scaling laws.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge