Lenient Regret and Good-Action Identification in Gaussian Process Bandits
Paper and Code
Feb 11, 2021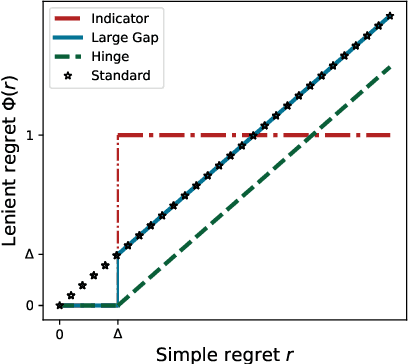
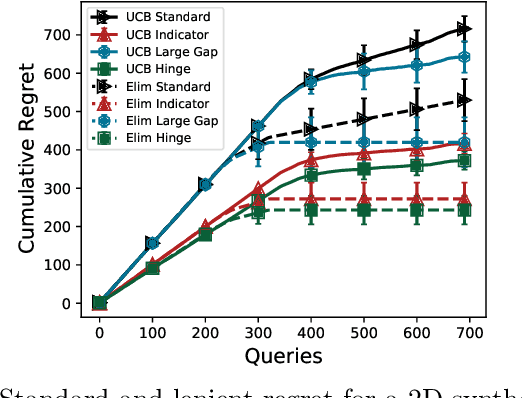
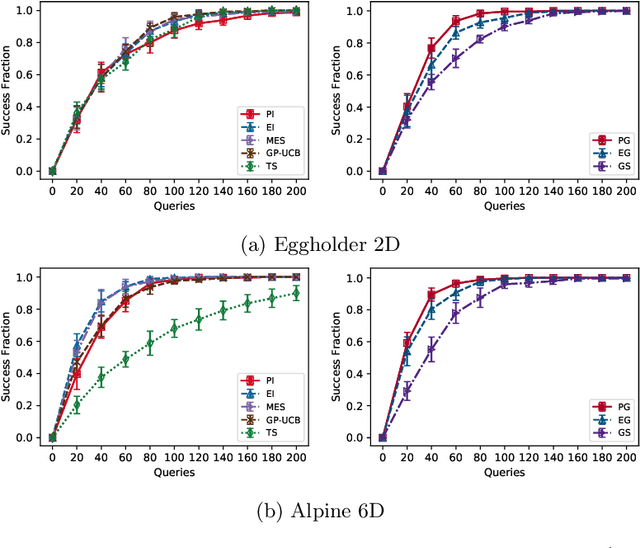

In this paper, we study the problem of Gaussian process (GP) bandits under relaxed optimization criteria stating that any function value above a certain threshold is "good enough". On the theoretical side, we study various \emph{\lenient regret} notions in which all near-optimal actions incur zero penalty, and provide upper bounds on the lenient regret for GP-UCB and an elimination algorithm, circumventing the usual $O(\sqrt{T})$ term (with time horizon $T$) resulting from zooming extremely close towards the function maximum. In addition, we complement these upper bounds with algorithm-independent lower bounds. On the practical side, we consider the problem of finding a single "good action" according to a known pre-specified threshold, and introduce several good-action identification algorithms that exploit knowledge of the threshold. We experimentally find that such algorithms can often find a good action faster than standard optimization-based approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge