Knowledge Transfer across Multiple Principal Component Analysis Studies

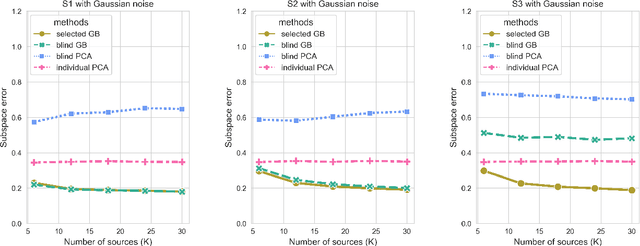
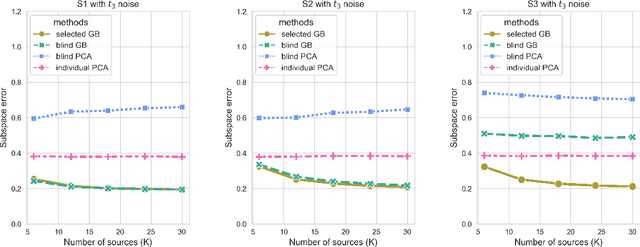
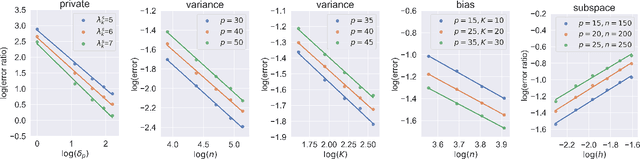
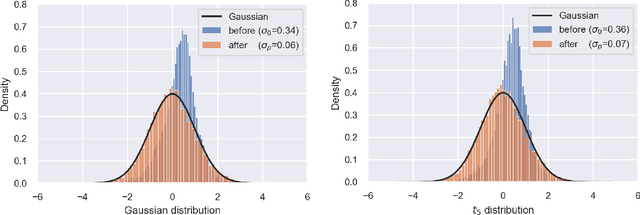
Transfer learning has aroused great interest in the statistical community. In this article, we focus on knowledge transfer for unsupervised learning tasks in contrast to the supervised learning tasks in the literature. Given the transferable source populations, we propose a two-step transfer learning algorithm to extract useful information from multiple source principal component analysis (PCA) studies, thereby enhancing estimation accuracy for the target PCA task. In the first step, we integrate the shared subspace information across multiple studies by a proposed method named as Grassmannian barycenter, instead of directly performing PCA on the pooled dataset. The proposed Grassmannian barycenter method enjoys robustness and computational advantages in more general cases. Then the resulting estimator for the shared subspace from the first step is further utilized to estimate the target private subspace in the second step. Our theoretical analysis credits the gain of knowledge transfer between PCA studies to the enlarged eigenvalue gap, which is different from the existing supervised transfer learning tasks where sparsity plays the central role. In addition, we prove that the bilinear forms of the empirical spectral projectors have asymptotic normality under weaker eigenvalue gap conditions after knowledge transfer. When the set of informativesources is unknown, we endow our algorithm with the capability of useful dataset selection by solving a rectified optimization problem on the Grassmann manifold, which in turn leads to a computationally friendly rectified Grassmannian K-means procedure. In the end, extensive numerical simulation results and a real data case concerning activity recognition are reported to support our theoretical claims and to illustrate the empirical usefulness of the proposed transfer learning methods.

D$^2$-City: A Large-Scale Dashcam Video Dataset of Diverse Traffic Scenarios

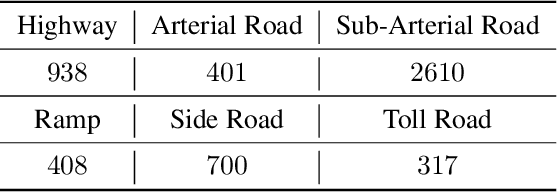
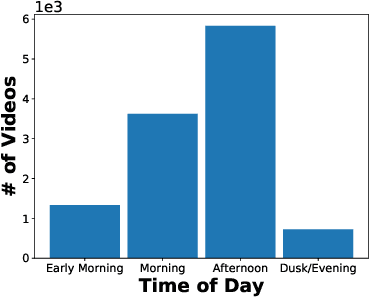
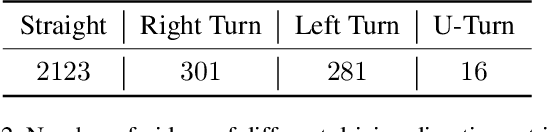
Driving datasets accelerate the development of intelligent driving and related computer vision technologies, while substantial and detailed annotations serve as fuels and powers to boost the efficacy of such datasets to improve learning-based models. We propose D$^2$-City, a large-scale comprehensive collection of dashcam videos collected by vehicles on DiDi's platform. D$^2$-City contains more than 10000 video clips which deeply reflect the diversity and complexity of real-world traffic scenarios in China. We also provide bounding boxes and tracking annotations of 12 classes of objects in all frames of 1000 videos and detection annotations on keyframes for the remainder of the videos. Compared with existing datasets, D$^2$-City features data in varying weather, road, and traffic conditions and a huge amount of elaborate detection and tracking annotations. By bringing a diverse set of challenging cases to the community, we expect the D$^2$-City dataset will advance the perception and related areas of intelligent driving.

An Extreme-Value Approach for Testing the Equality of Large U-Statistic Based Correlation Matrices

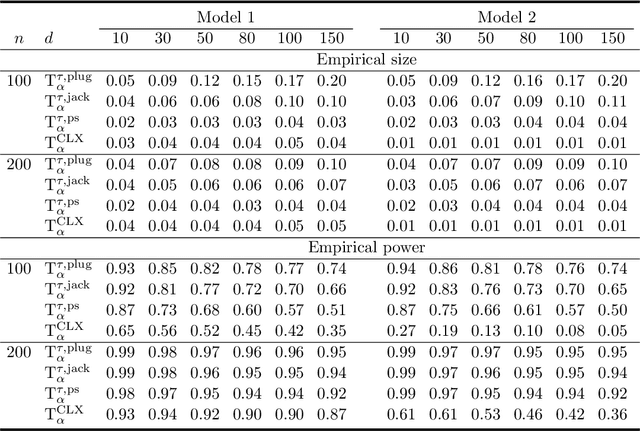
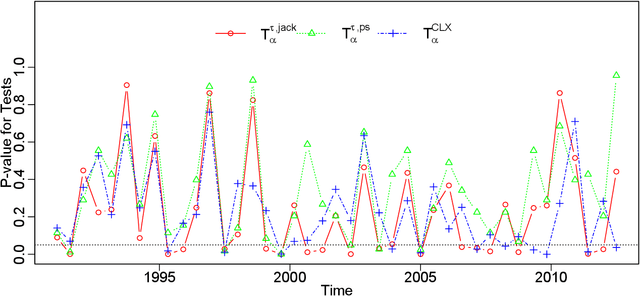
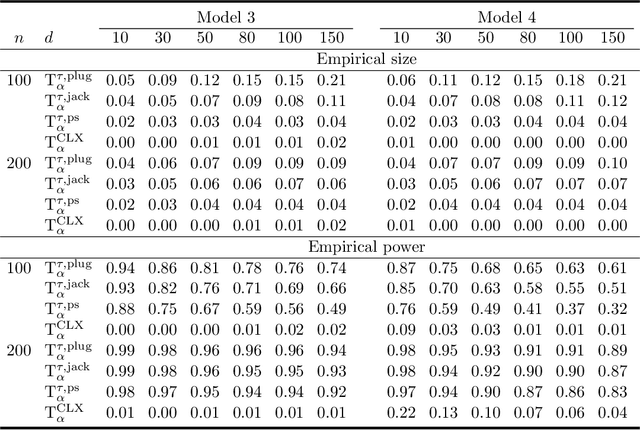
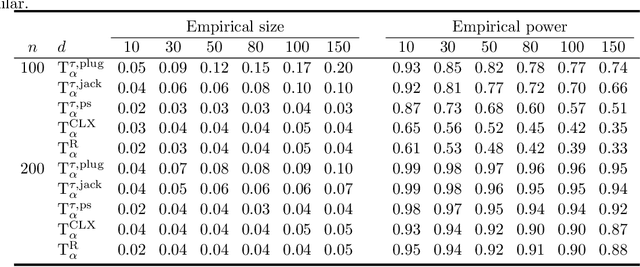
There has been an increasing interest in testing the equality of large Pearson's correlation matrices. However, in many applications it is more important to test the equality of large rank-based correlation matrices since they are more robust to outliers and nonlinearity. Unlike the Pearson's case, testing the equality of large rank-based statistics has not been well explored and requires us to develop new methods and theory. In this paper, we provide a framework for testing the equality of two large U-statistic based correlation matrices, which include the rank-based correlation matrices as special cases. Our approach exploits extreme value statistics and the Jackknife estimator for uncertainty assessment and is valid under a fully nonparametric model. Theoretically, we develop a theory for testing the equality of U-statistic based correlation matrices. We then apply this theory to study the problem of testing large Kendall's tau correlation matrices and demonstrate its optimality. For proving this optimality, a novel construction of least favourable distributions is developed for the correlation matrix comparison.