Representational Transfer Learning for Matrix Completion

We propose to transfer representational knowledge from multiple sources to a target noisy matrix completion task by aggregating singular subspaces information. Under our representational similarity framework, we first integrate linear representation information by solving a two-way principal component analysis problem based on a properly debiased matrix-valued dataset. After acquiring better column and row representation estimators from the sources, the original high-dimensional target matrix completion problem is then transformed into a low-dimensional linear regression, of which the statistical efficiency is guaranteed. A variety of extensional arguments, including post-transfer statistical inference and robustness against negative transfer, are also discussed alongside. Finally, extensive simulation results and a number of real data cases are reported to support our claims.

Knowledge Transfer across Multiple Principal Component Analysis Studies

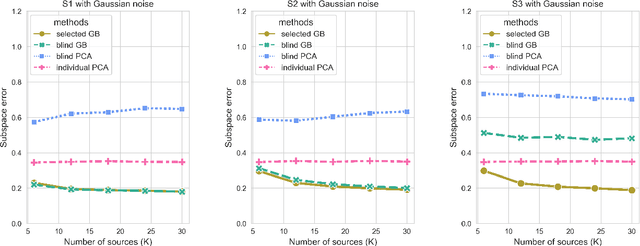
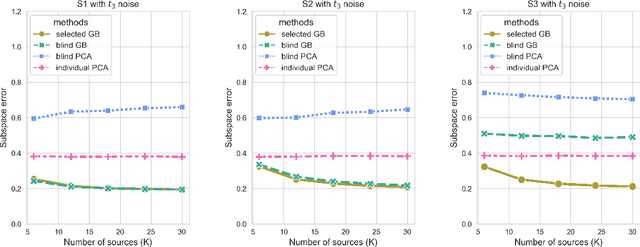
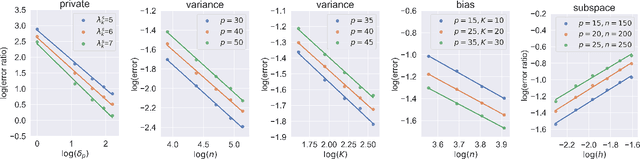
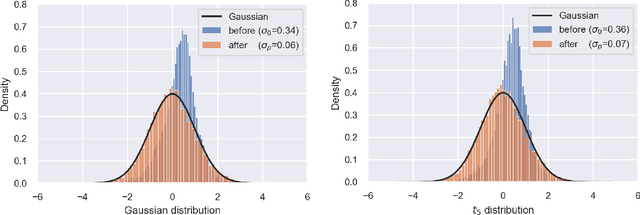
Transfer learning has aroused great interest in the statistical community. In this article, we focus on knowledge transfer for unsupervised learning tasks in contrast to the supervised learning tasks in the literature. Given the transferable source populations, we propose a two-step transfer learning algorithm to extract useful information from multiple source principal component analysis (PCA) studies, thereby enhancing estimation accuracy for the target PCA task. In the first step, we integrate the shared subspace information across multiple studies by a proposed method named as Grassmannian barycenter, instead of directly performing PCA on the pooled dataset. The proposed Grassmannian barycenter method enjoys robustness and computational advantages in more general cases. Then the resulting estimator for the shared subspace from the first step is further utilized to estimate the target private subspace in the second step. Our theoretical analysis credits the gain of knowledge transfer between PCA studies to the enlarged eigenvalue gap, which is different from the existing supervised transfer learning tasks where sparsity plays the central role. In addition, we prove that the bilinear forms of the empirical spectral projectors have asymptotic normality under weaker eigenvalue gap conditions after knowledge transfer. When the set of informativesources is unknown, we endow our algorithm with the capability of useful dataset selection by solving a rectified optimization problem on the Grassmann manifold, which in turn leads to a computationally friendly rectified Grassmannian K-means procedure. In the end, extensive numerical simulation results and a real data case concerning activity recognition are reported to support our theoretical claims and to illustrate the empirical usefulness of the proposed transfer learning methods.