An Extreme-Value Approach for Testing the Equality of Large U-Statistic Based Correlation Matrices
Paper and Code
Mar 30, 2018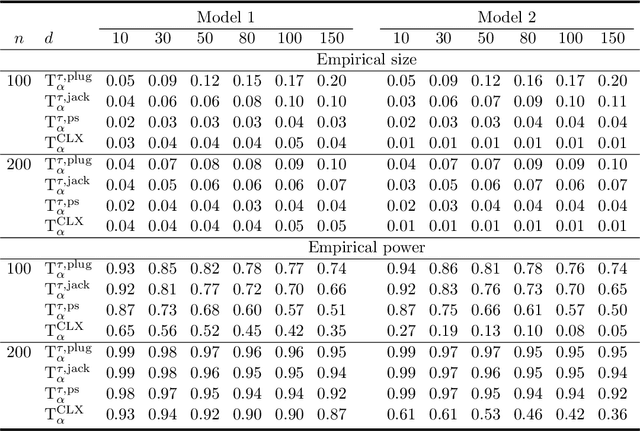
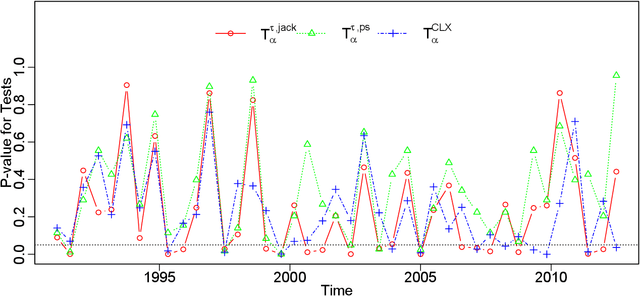
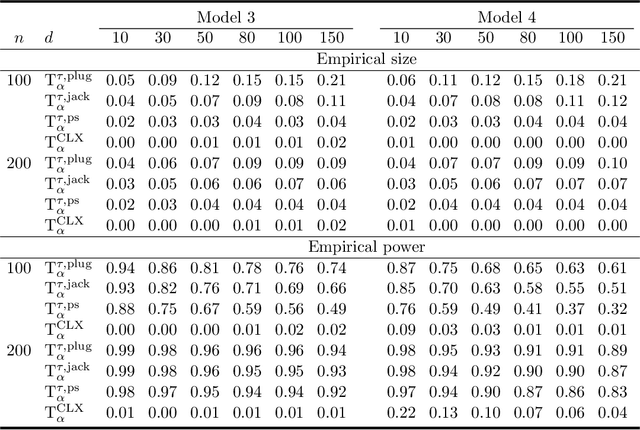
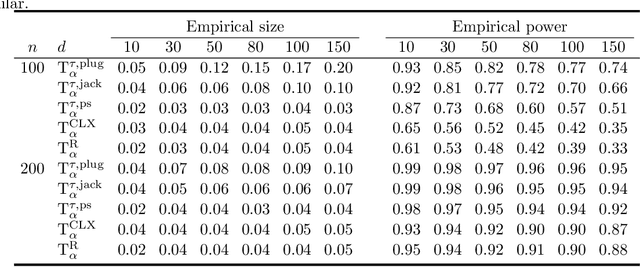
There has been an increasing interest in testing the equality of large Pearson's correlation matrices. However, in many applications it is more important to test the equality of large rank-based correlation matrices since they are more robust to outliers and nonlinearity. Unlike the Pearson's case, testing the equality of large rank-based statistics has not been well explored and requires us to develop new methods and theory. In this paper, we provide a framework for testing the equality of two large U-statistic based correlation matrices, which include the rank-based correlation matrices as special cases. Our approach exploits extreme value statistics and the Jackknife estimator for uncertainty assessment and is valid under a fully nonparametric model. Theoretically, we develop a theory for testing the equality of U-statistic based correlation matrices. We then apply this theory to study the problem of testing large Kendall's tau correlation matrices and demonstrate its optimality. For proving this optimality, a novel construction of least favourable distributions is developed for the correlation matrix comparison.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge