Niagara: Normal-Integrated Geometric Affine Field for Scene Reconstruction from a Single View

Recent advances in single-view 3D scene reconstruction have highlighted the challenges in capturing fine geometric details and ensuring structural consistency, particularly in high-fidelity outdoor scene modeling. This paper presents Niagara, a new single-view 3D scene reconstruction framework that can faithfully reconstruct challenging outdoor scenes from a single input image for the first time. Our approach integrates monocular depth and normal estimation as input, which substantially improves its ability to capture fine details, mitigating common issues like geometric detail loss and deformation. Additionally, we introduce a geometric affine field (GAF) and 3D self-attention as geometry-constraint, which combines the structural properties of explicit geometry with the adaptability of implicit feature fields, striking a balance between efficient rendering and high-fidelity reconstruction. Our framework finally proposes a specialized encoder-decoder architecture, where a depth-based 3D Gaussian decoder is proposed to predict 3D Gaussian parameters, which can be used for novel view synthesis. Extensive results and analyses suggest that our Niagara surpasses prior SoTA approaches such as Flash3D in both single-view and dual-view settings, significantly enhancing the geometric accuracy and visual fidelity, especially in outdoor scenes.

LightGen: Efficient Image Generation through Knowledge Distillation and Direct Preference Optimization

Recent advances in text-to-image generation have primarily relied on extensive datasets and parameter-heavy architectures. These requirements severely limit accessibility for researchers and practitioners who lack substantial computational resources. In this paper, we introduce \model, an efficient training paradigm for image generation models that uses knowledge distillation (KD) and Direct Preference Optimization (DPO). Drawing inspiration from the success of data KD techniques widely adopted in Multi-Modal Large Language Models (MLLMs), LightGen distills knowledge from state-of-the-art (SOTA) text-to-image models into a compact Masked Autoregressive (MAR) architecture with only $0.7B$ parameters. Using a compact synthetic dataset of just $2M$ high-quality images generated from varied captions, we demonstrate that data diversity significantly outweighs data volume in determining model performance. This strategy dramatically reduces computational demands and reduces pre-training time from potentially thousands of GPU-days to merely 88 GPU-days. Furthermore, to address the inherent shortcomings of synthetic data, particularly poor high-frequency details and spatial inaccuracies, we integrate the DPO technique that refines image fidelity and positional accuracy. Comprehensive experiments confirm that LightGen achieves image generation quality comparable to SOTA models while significantly reducing computational resources and expanding accessibility for resource-constrained environments. Code is available at https://github.com/XianfengWu01/LightGen

FSC: Few-point Shape Completion

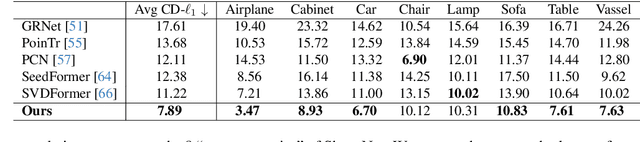
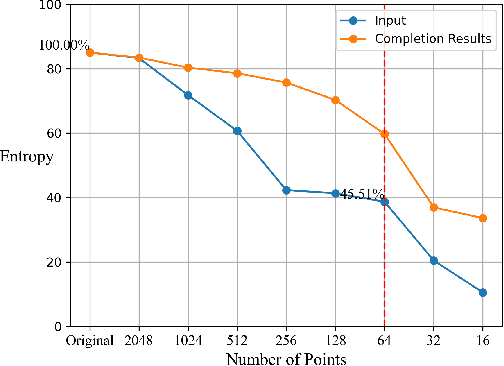
While previous studies have demonstrated successful 3D object shape completion with a sufficient number of points, they often fail in scenarios when a few points, e.g. tens of points, are observed. Surprisingly, via entropy analysis, we find that even a few points, e.g. 64 points, could retain substantial information to help recover the 3D shape of the object. To address the challenge of shape completion with very sparse point clouds, we then propose Few-point Shape Completion (FSC) model, which contains a novel dual-branch feature extractor for handling extremely sparse inputs, coupled with an extensive branch for maximal point utilization with a saliency branch for dynamic importance assignment. This model is further bolstered by a two-stage revision network that refines both the extracted features and the decoder output, enhancing the detail and authenticity of the completed point cloud. Our experiments demonstrate the feasibility of recovering 3D shapes from a few points. The proposed Few-point Shape Completion (FSC) model outperforms previous methods on both few-point inputs and many-point inputs, and shows good generalizability to different object categories.

Completing point cloud from few points by Wasserstein GAN and Transformers

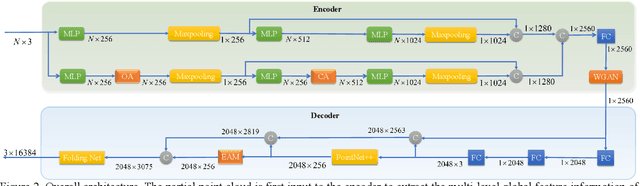
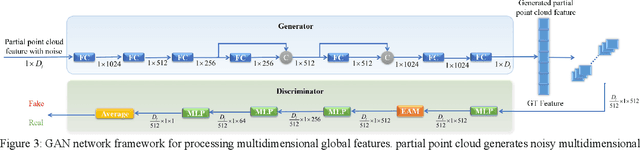
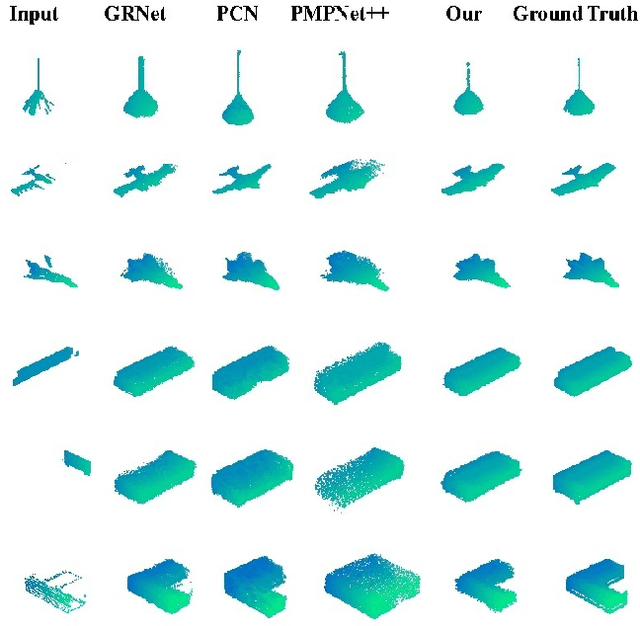
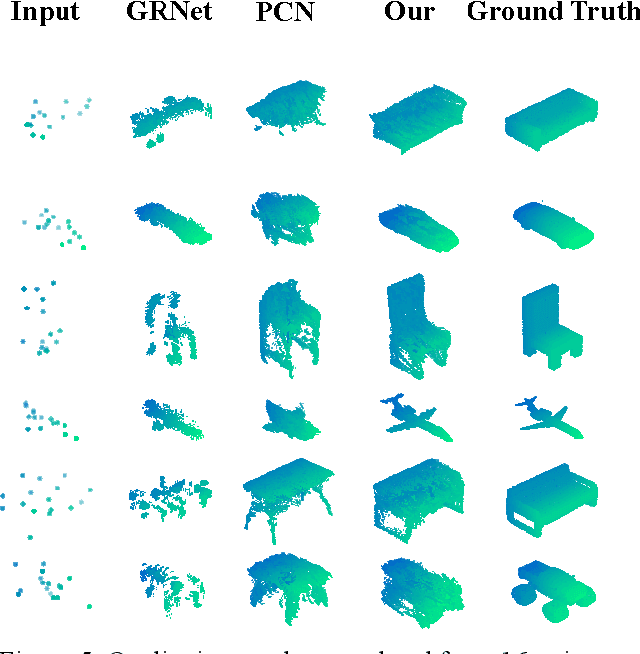
In many vision and robotics applications, it is common that the captured objects are represented by very few points. Most of the existing completion methods are designed for partial point clouds with many points, and they perform poorly or even fail completely in the case of few points. However, due to the lack of detail information, completing objects from few points faces a huge challenge. Inspired by the successful applications of GAN and Transformers in the image-based vision task, we introduce GAN and Transformer techniques to address the above problem. Firstly, the end-to-end encoder-decoder network with Transformers and the Wasserstein GAN with Transformer are pre-trained, and then the overall network is fine-tuned. Experimental results on the ShapeNet dataset show that our method can not only improve the completion performance for many input points, but also keep stable for few input points. Our source code is available at https://github.com/WxfQjh/Stability-point-recovery.git.