From Tissue Plane to Organ World: A Benchmark Dataset for Multimodal Biomedical Image Registration using Deep Co-Attention Networks

Correlating neuropathology with neuroimaging findings provides a multiscale view of pathologic changes in the human organ spanning the meso- to micro-scales, and is an emerging methodology expected to shed light on numerous disease states. To gain the most information from this multimodal, multiscale approach, it is desirable to identify precisely where a histologic tissue section was taken from within the organ in order to correlate with the tissue features in exactly the same organ region. Histology-to-organ registration poses an extra challenge, as any given histologic section can capture only a small portion of a human organ. Making use of the capabilities of state-of-the-art deep learning models, we unlock the potential to address and solve such intricate challenges. Therefore, we create the ATOM benchmark dataset, sourced from diverse institutions, with the primary objective of transforming this challenge into a machine learning problem and delivering outstanding outcomes that enlighten the biomedical community. The performance of our RegisMCAN model demonstrates the potential of deep learning to accurately predict where a subregion extracted from an organ image was obtained from within the overall 3D volume. The code and dataset can be found at: https://github.com/haizailache999/Image-Registration/tree/main

A hybrid Decoder-DeepONet operator regression framework for unaligned observation data

Deep neural operators (DNOs) have been utilized to approximate nonlinear mappings between function spaces. However, DNOs face the challenge of increased dimensionality and computational cost associated with unaligned observation data. In this study, we propose a hybrid Decoder-DeepONet operator regression framework to handle unaligned data effectively. Additionally, we introduce a Multi-Decoder-DeepONet, which utilizes an average field of training data as input augmentation. The consistencies of the frameworks with the operator approximation theory are provided, on the basis of the universal approximation theorem. Two numerical experiments, Darcy problem and flow-field around an airfoil, are conducted to validate the efficiency and accuracy of the proposed methods. Results illustrate the advantages of Decoder-DeepONet and Multi-Decoder-DeepONet in handling unaligned observation data and showcase their potentials in improving prediction accuracy.

Using AntiPatterns to avoid MLOps Mistakes

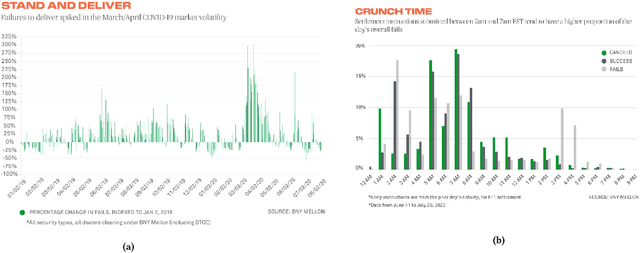
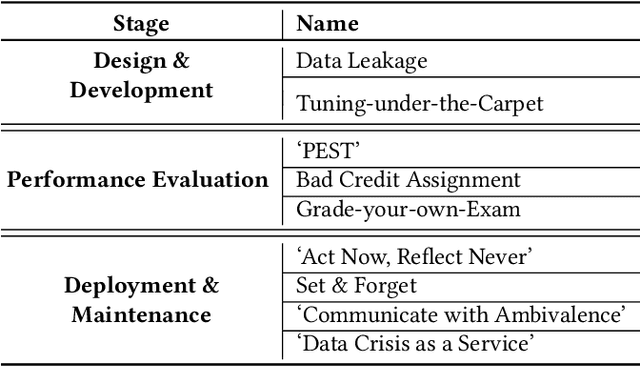
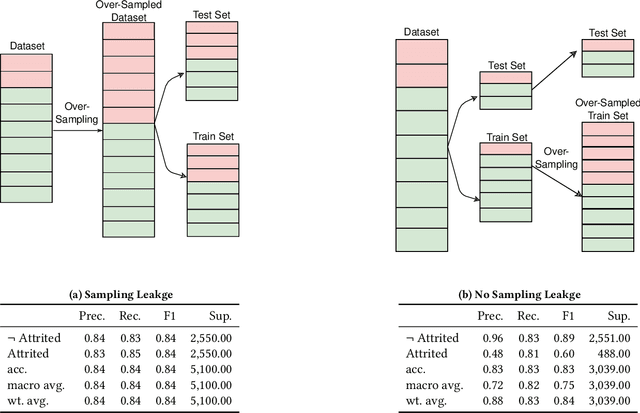
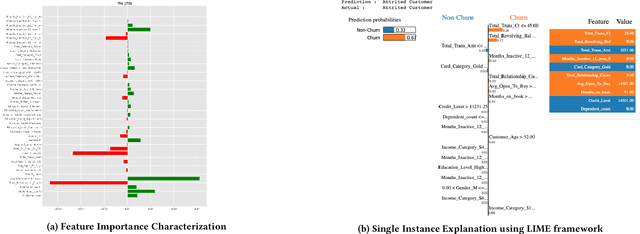
We describe lessons learned from developing and deploying machine learning models at scale across the enterprise in a range of financial analytics applications. These lessons are presented in the form of antipatterns. Just as design patterns codify best software engineering practices, antipatterns provide a vocabulary to describe defective practices and methodologies. Here we catalog and document numerous antipatterns in financial ML operations (MLOps). Some antipatterns are due to technical errors, while others are due to not having sufficient knowledge of the surrounding context in which ML results are used. By providing a common vocabulary to discuss these situations, our intent is that antipatterns will support better documentation of issues, rapid communication between stakeholders, and faster resolution of problems. In addition to cataloging antipatterns, we describe solutions, best practices, and future directions toward MLOps maturity.

Training Sparse Neural Network by Constraining Synaptic Weight on Unit Lp Sphere

Sparse deep neural networks have shown their advantages over dense models with fewer parameters and higher computational efficiency. Here we demonstrate constraining the synaptic weights on unit Lp-sphere enables the flexibly control of the sparsity with p and improves the generalization ability of neural networks. Firstly, to optimize the synaptic weights constrained on unit Lp-sphere, the parameter optimization algorithm, Lp-spherical gradient descent (LpSGD) is derived from the augmented Empirical Risk Minimization condition, which is theoretically proved to be convergent. To understand the mechanism of how p affects Hoyer's sparsity, the expectation of Hoyer's sparsity under the hypothesis of gamma distribution is given and the predictions are verified at various p under different conditions. In addition, the "semi-pruning" and threshold adaptation are designed for topology evolution to effectively screen out important connections and lead the neural networks converge from the initial sparsity to the expected sparsity. Our approach is validated by experiments on benchmark datasets covering a wide range of domains. And the theoretical analysis pave the way to future works on training sparse neural networks with constrained optimization.