A hybrid Decoder-DeepONet operator regression framework for unaligned observation data

Deep neural operators (DNOs) have been utilized to approximate nonlinear mappings between function spaces. However, DNOs face the challenge of increased dimensionality and computational cost associated with unaligned observation data. In this study, we propose a hybrid Decoder-DeepONet operator regression framework to handle unaligned data effectively. Additionally, we introduce a Multi-Decoder-DeepONet, which utilizes an average field of training data as input augmentation. The consistencies of the frameworks with the operator approximation theory are provided, on the basis of the universal approximation theorem. Two numerical experiments, Darcy problem and flow-field around an airfoil, are conducted to validate the efficiency and accuracy of the proposed methods. Results illustrate the advantages of Decoder-DeepONet and Multi-Decoder-DeepONet in handling unaligned observation data and showcase their potentials in improving prediction accuracy.

Data-Driven Modeling of Landau Damping by Physics-Informed Neural Networks

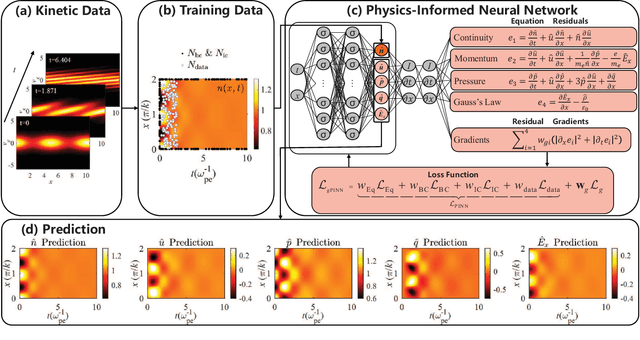
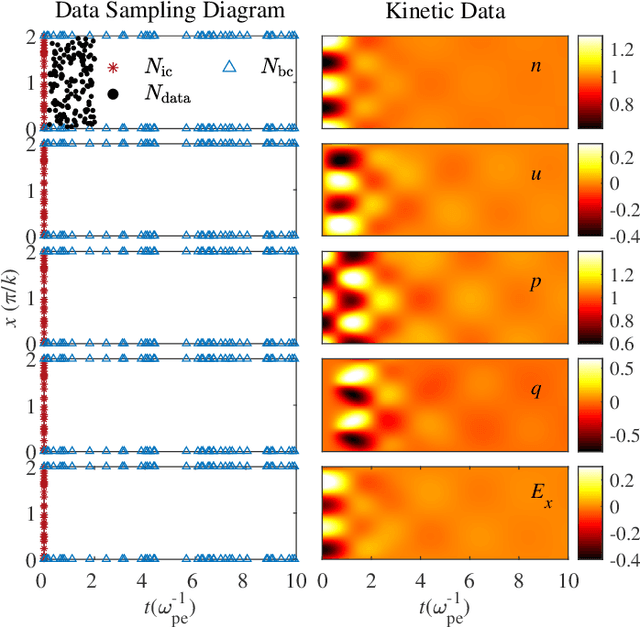
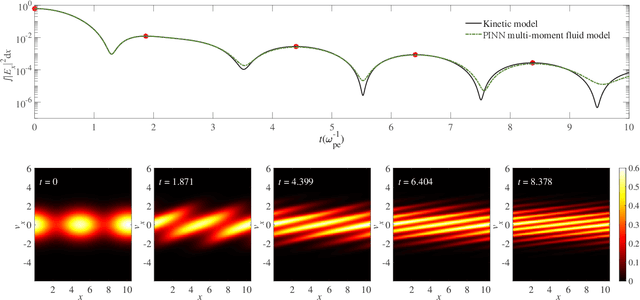
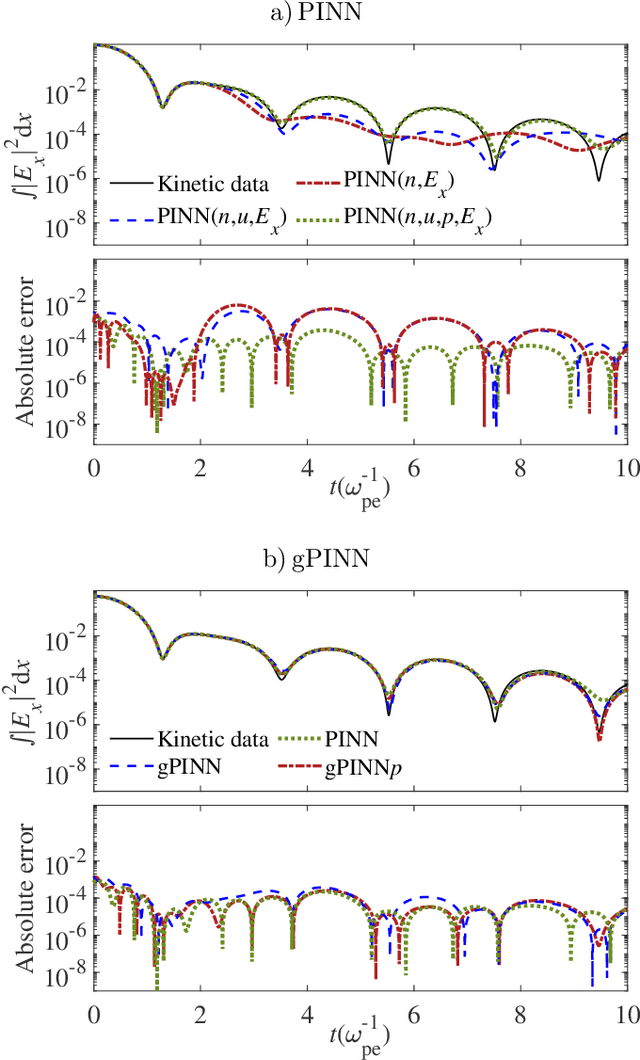
Kinetic approaches are generally accurate in dealing with microscale plasma physics problems but are computationally expensive for large-scale or multiscale systems. One of the long-standing problems in plasma physics is the integration of kinetic physics into fluid models, which is often achieved through sophisticated analytical closure terms. In this study, we successfully construct a multi-moment fluid model with an implicit fluid closure included in the neural network using machine learning. The multi-moment fluid model is trained with a small fraction of sparsely sampled data from kinetic simulations of Landau damping, using the physics-informed neural network (PINN) and the gradient-enhanced physics-informed neural network (gPINN). The multi-moment fluid model constructed using either PINN or gPINN reproduces the time evolution of the electric field energy, including its damping rate, and the plasma dynamics from the kinetic simulations. For the first time, we introduce a new variant of the gPINN architecture, namely, gPINN$p$ to capture the Landau damping process. Instead of including the gradients of all the equation residuals, gPINN$p$ only adds the gradient of the pressure equation residual as one additional constraint. Among the three approaches, the gPINN$p$-constructed multi-moment fluid model offers the most accurate results. This work sheds new light on the accurate and efficient modeling of large-scale systems, which can be extended to complex multiscale laboratory, space, and astrophysical plasma physics problems.

Data-driven, multi-moment fluid modeling of Landau damping

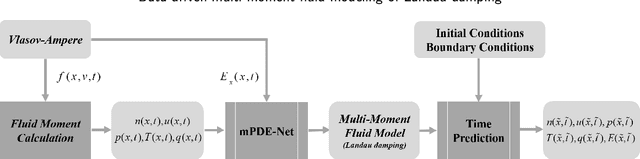
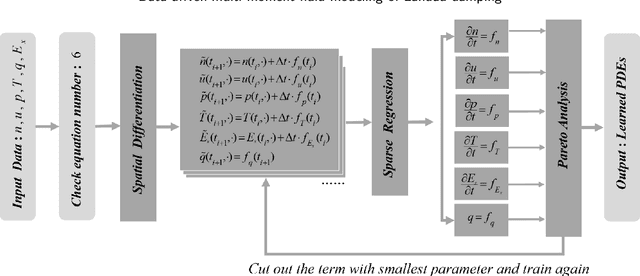
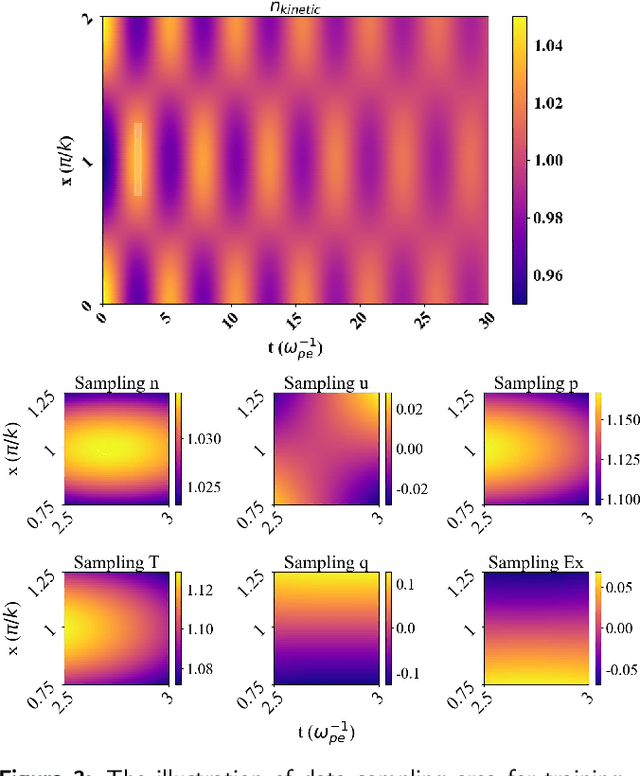
Deriving governing equations of complex physical systems based on first principles can be quite challenging when there are certain unknown terms and hidden physical mechanisms in the systems. In this work, we apply a deep learning architecture to learn fluid partial differential equations (PDEs) of a plasma system based on the data acquired from a fully kinetic model. The learned multi-moment fluid PDEs are demonstrated to incorporate kinetic effects such as Landau damping. Based on the learned fluid closure, the data-driven, multi-moment fluid modeling can well reproduce all the physical quantities derived from the fully kinetic model. The calculated damping rate of Landau damping is consistent with both the fully kinetic simulation and the linear theory. The data-driven fluid modeling of PDEs for complex physical systems may be applied to improve fluid closure and reduce the computational cost of multi-scale modeling of global systems.