Conceptual Study and Performance Analysis of Tandem Dual-Antenna Spaceborne SAR Interferometry

Multi-baseline synthetic aperture radar interferometry (MB-InSAR), capable of mapping 3D surface model with high precision, is able to overcome the ill-posed problem in the single-baseline InSAR by use of the baseline diversity. Single pass MB acquisition with the advantages of high coherence and simple phase components has a more practical capability in 3D reconstruction than conventional repeat-pass MB acquisition. Using an asymptotic 3D phase unwrapping (PU), it is possible to get a reliable 3D reconstruction using very sparse acquisitions but the interferograms should follow the optimal baseline design. However, current spaceborne SAR system doesn't satisfy this principle, inducing more difficulties in practical application. In this article, a new concept of Tandem Dual-Antenna SAR Interferometry (TDA-InSAR) system for single-pass reliable 3D surface mapping using the asymptotic 3D PU is proposed. Its optimal MB acquisition is analyzed to achieve both good relative height precision and flexible baseline design. Two indicators, i.e., expected relative height precision and successful phase unwrapping rate, are selected to optimize the system parameters and evaluate the performance of various baseline configurations. Additionally, simulation-based demonstrations are conducted to evaluate the performance in typical scenarios and investigate the impact of various error sources. The results indicate that the proposed TDA-InSAR is able to get the specified MB acquisition for the asymptotic 3D PU, which offers a feasible solution for single-pass 3D SAR imaging.

Data-Driven Modeling of Landau Damping by Physics-Informed Neural Networks

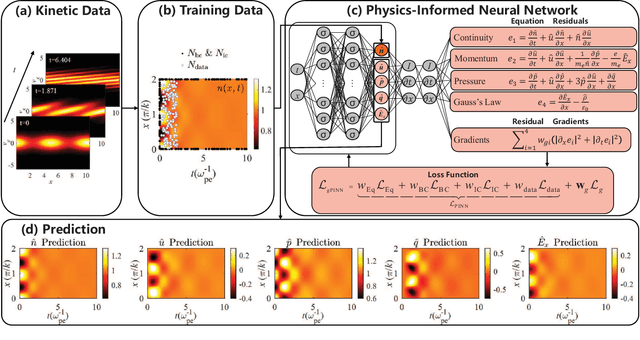
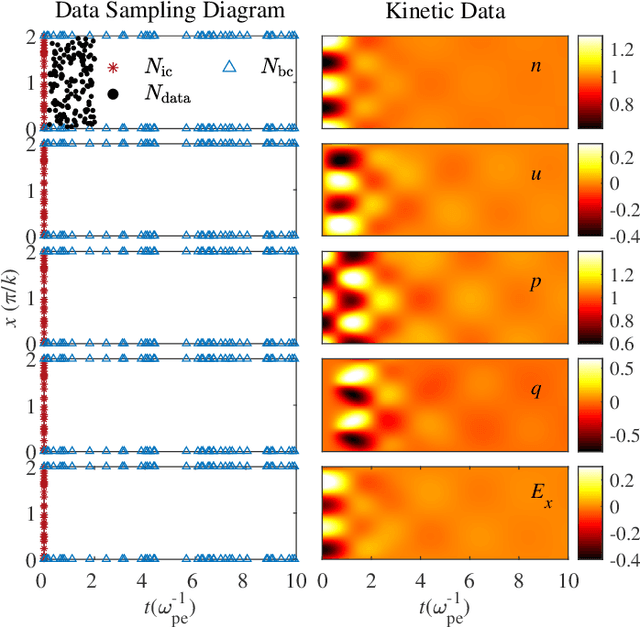
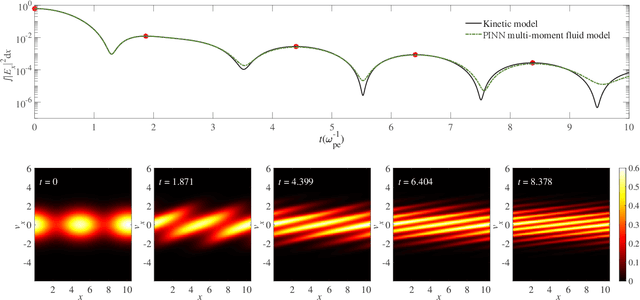
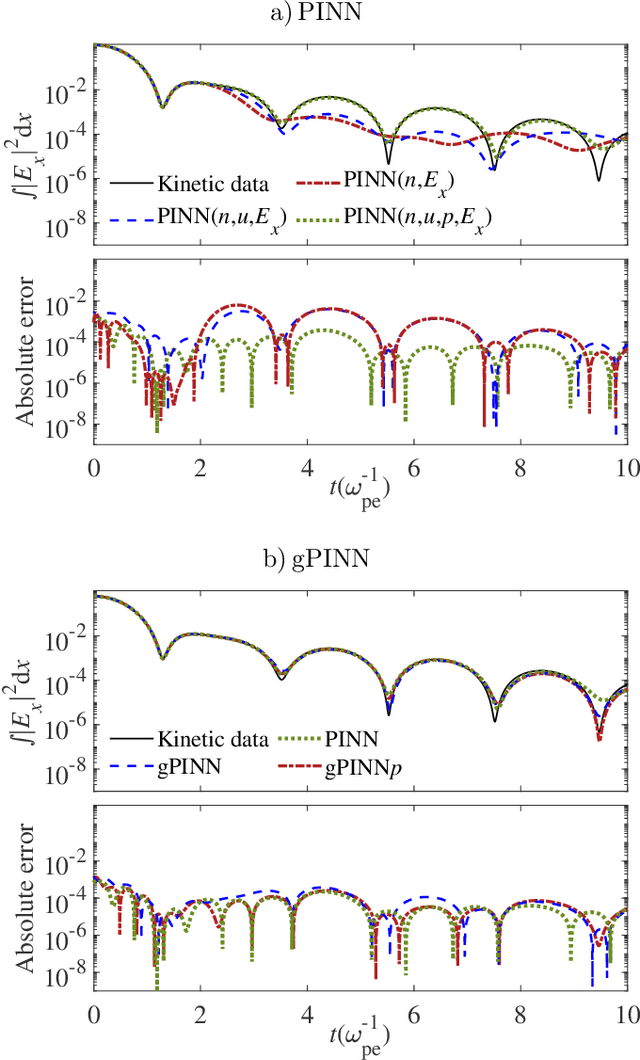
Kinetic approaches are generally accurate in dealing with microscale plasma physics problems but are computationally expensive for large-scale or multiscale systems. One of the long-standing problems in plasma physics is the integration of kinetic physics into fluid models, which is often achieved through sophisticated analytical closure terms. In this study, we successfully construct a multi-moment fluid model with an implicit fluid closure included in the neural network using machine learning. The multi-moment fluid model is trained with a small fraction of sparsely sampled data from kinetic simulations of Landau damping, using the physics-informed neural network (PINN) and the gradient-enhanced physics-informed neural network (gPINN). The multi-moment fluid model constructed using either PINN or gPINN reproduces the time evolution of the electric field energy, including its damping rate, and the plasma dynamics from the kinetic simulations. For the first time, we introduce a new variant of the gPINN architecture, namely, gPINN$p$ to capture the Landau damping process. Instead of including the gradients of all the equation residuals, gPINN$p$ only adds the gradient of the pressure equation residual as one additional constraint. Among the three approaches, the gPINN$p$-constructed multi-moment fluid model offers the most accurate results. This work sheds new light on the accurate and efficient modeling of large-scale systems, which can be extended to complex multiscale laboratory, space, and astrophysical plasma physics problems.

Data-driven, multi-moment fluid modeling of Landau damping

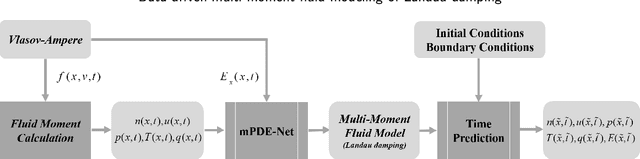
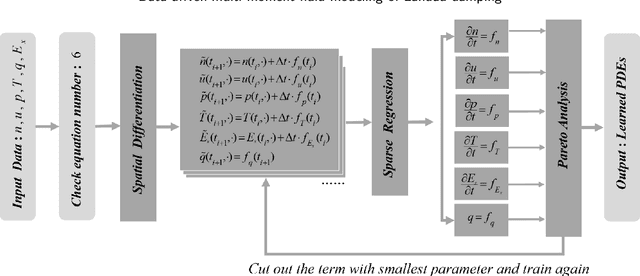
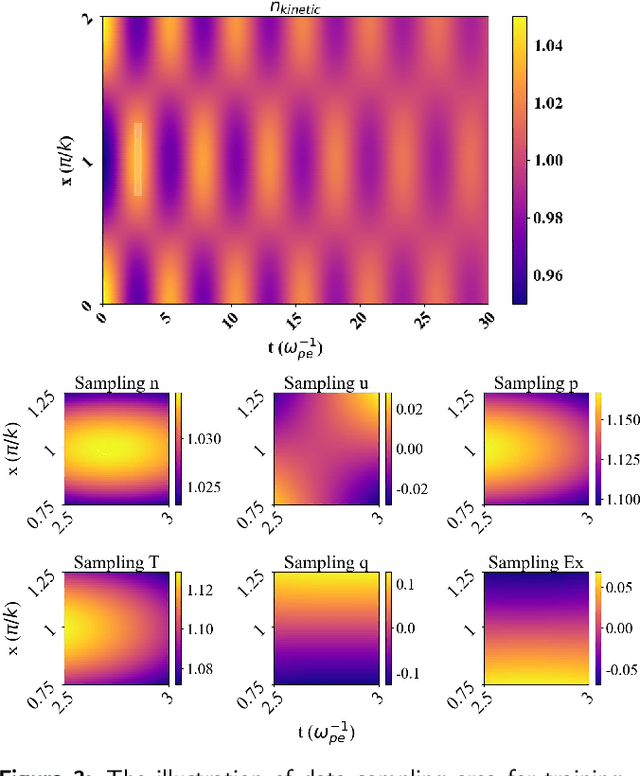
Deriving governing equations of complex physical systems based on first principles can be quite challenging when there are certain unknown terms and hidden physical mechanisms in the systems. In this work, we apply a deep learning architecture to learn fluid partial differential equations (PDEs) of a plasma system based on the data acquired from a fully kinetic model. The learned multi-moment fluid PDEs are demonstrated to incorporate kinetic effects such as Landau damping. Based on the learned fluid closure, the data-driven, multi-moment fluid modeling can well reproduce all the physical quantities derived from the fully kinetic model. The calculated damping rate of Landau damping is consistent with both the fully kinetic simulation and the linear theory. The data-driven fluid modeling of PDEs for complex physical systems may be applied to improve fluid closure and reduce the computational cost of multi-scale modeling of global systems.