A Robust Prototype-Based Network with Interpretable RBF Classifier Foundations

Prototype-based classification learning methods are known to be inherently interpretable. However, this paradigm suffers from major limitations compared to deep models, such as lower performance. This led to the development of the so-called deep Prototype-Based Networks (PBNs), also known as prototypical parts models. In this work, we analyze these models with respect to different properties, including interpretability. In particular, we focus on the Classification-by-Components (CBC) approach, which uses a probabilistic model to ensure interpretability and can be used as a shallow or deep architecture. We show that this model has several shortcomings, like creating contradicting explanations. Based on these findings, we propose an extension of CBC that solves these issues. Moreover, we prove that this extension has robustness guarantees and derive a loss that optimizes robustness. Additionally, our analysis shows that most (deep) PBNs are related to (deep) RBF classifiers, which implies that our robustness guarantees generalize to shallow RBF classifiers. The empirical evaluation demonstrates that our deep PBN yields state-of-the-art classification accuracy on different benchmarks while resolving the interpretability shortcomings of other approaches. Further, our shallow PBN variant outperforms other shallow PBNs while being inherently interpretable and exhibiting provable robustness guarantees.

Aligning Generalisation Between Humans and Machines

Recent advances in AI -- including generative approaches -- have resulted in technology that can support humans in scientific discovery and decision support but may also disrupt democracies and target individuals. The responsible use of AI increasingly shows the need for human-AI teaming, necessitating effective interaction between humans and machines. A crucial yet often overlooked aspect of these interactions is the different ways in which humans and machines generalise. In cognitive science, human generalisation commonly involves abstraction and concept learning. In contrast, AI generalisation encompasses out-of-domain generalisation in machine learning, rule-based reasoning in symbolic AI, and abstraction in neuro-symbolic AI. In this perspective paper, we combine insights from AI and cognitive science to identify key commonalities and differences across three dimensions: notions of generalisation, methods for generalisation, and evaluation of generalisation. We map the different conceptualisations of generalisation in AI and cognitive science along these three dimensions and consider their role in human-AI teaming. This results in interdisciplinary challenges across AI and cognitive science that must be tackled to provide a foundation for effective and cognitively supported alignment in human-AI teaming scenarios.

Robustness of Generalized Learning Vector Quantization Models against Adversarial Attacks

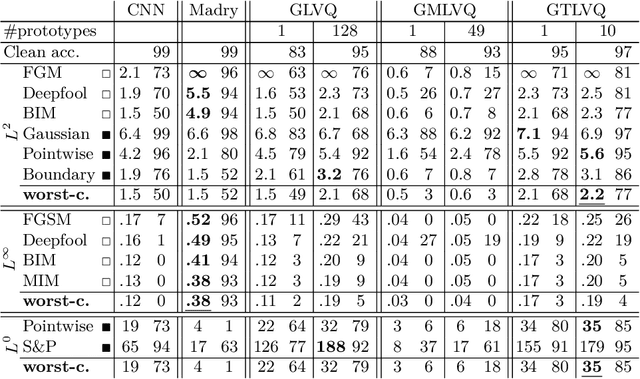
Adversarial attacks and the development of (deep) neural networks robust against them are currently two widely researched topics. The robustness of Learning Vector Quantization (LVQ) models against adversarial attacks has however not yet been studied to the same extent. We therefore present an extensive evaluation of three LVQ models: Generalized LVQ, Generalized Matrix LVQ and Generalized Tangent LVQ. The evaluation suggests that both Generalized LVQ and Generalized Tangent LVQ have a high base robustness, on par with the current state-of-the-art in robust neural network methods. In contrast to this, Generalized Matrix LVQ shows a high susceptibility to adversarial attacks, scoring consistently behind all other models. Additionally, our numerical evaluation indicates that increasing the number of prototypes per class improves the robustness of the models.

Prototype-based Neural Network Layers: Incorporating Vector Quantization

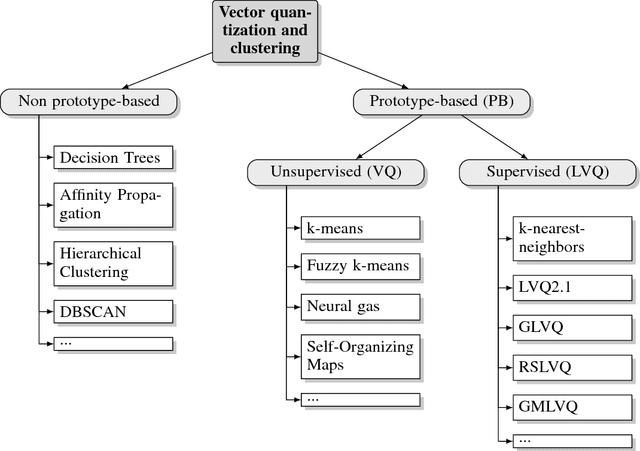
Neural networks currently dominate the machine learning community and they do so for good reasons. Their accuracy on complex tasks such as image classification is unrivaled at the moment and with recent improvements they are reasonably easy to train. Nevertheless, neural networks are lacking robustness and interpretability. Prototype-based vector quantization methods on the other hand are known for being robust and interpretable. For this reason, we propose techniques and strategies to merge both approaches. This contribution will particularly highlight the similarities between them and outline how to construct a prototype-based classification layer for multilayer networks. Additionally, we provide an alternative, prototype-based, approach to the classical convolution operation. Numerical results are not part of this report, instead the focus lays on establishing a strong theoretical framework. By publishing our framework and the respective theoretical considerations and justifications before finalizing our numerical experiments we hope to jump-start the incorporation of prototype-based learning in neural networks and vice versa.

Activation Functions for Generalized Learning Vector Quantization - A Performance Comparison

An appropriate choice of the activation function (like ReLU, sigmoid or swish) plays an important role in the performance of (deep) multilayer perceptrons (MLP) for classification and regression learning. Prototype-based classification learning methods like (generalized) learning vector quantization (GLVQ) are powerful alternatives. These models also deal with activation functions but here they are applied to the so-called classifier function instead. In this paper we investigate successful candidates of activation functions known for MLPs for application in GLVQ and their influence on the performance.

Regularization in Relevance Learning Vector Quantization Using l one Norms

We propose in this contribution a method for l one regularization in prototype based relevance learning vector quantization (LVQ) for sparse relevance profiles. Sparse relevance profiles in hyperspectral data analysis fade down those spectral bands which are not necessary for classification. In particular, we consider the sparsity in the relevance profile enforced by LASSO optimization. The latter one is obtained by a gradient learning scheme using a differentiable parametrized approximation of the $l_{1}$-norm, which has an upper error bound. We extend this regularization idea also to the matrix learning variant of LVQ as the natural generalization of relevance learning.