Path Integral Stochastic Optimal Control for Sampling Transition Paths

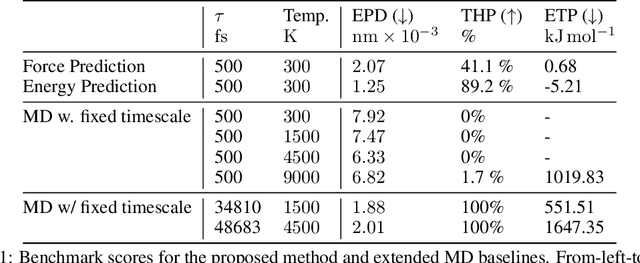
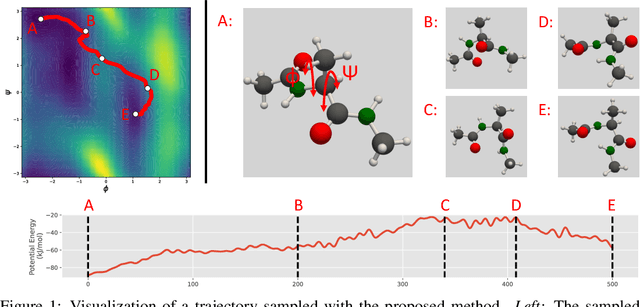
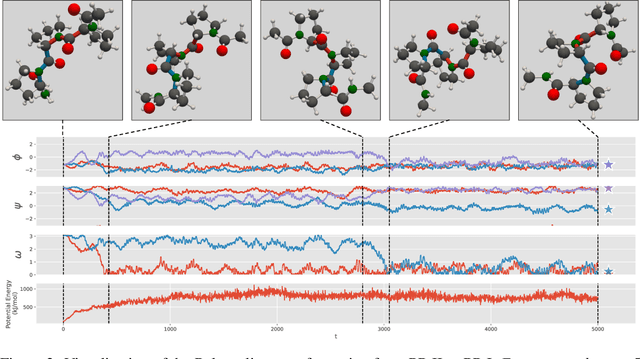
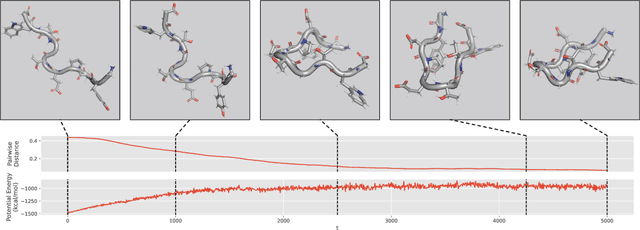
We consider the problem of Sampling Transition Paths. Given two metastable conformational states of a molecular system, eg. a folded and unfolded protein, we aim to sample the most likely transition path between the two states. Sampling such a transition path is computationally expensive due to the existence of high free energy barriers between the two states. To circumvent this, previous work has focused on simplifying the trajectories to occur along specific molecular descriptors called Collective Variables (CVs). However, finding CVs is not trivial and requires chemical intuition. For larger molecules, where intuition is not sufficient, using these CV-based methods biases the transition along possibly irrelevant dimensions. Instead, this work proposes a method for sampling transition paths that consider the entire geometry of the molecules. To achieve this, we first relate the problem to recent work on the Schrodinger bridge problem and stochastic optimal control. Using this relation, we construct a method that takes into account important characteristics of molecular systems such as second-order dynamics and invariance to rotations and translations. We demonstrate our method on the commonly studied Alanine Dipeptide, but also consider larger proteins such as Polyproline and Chignolin.

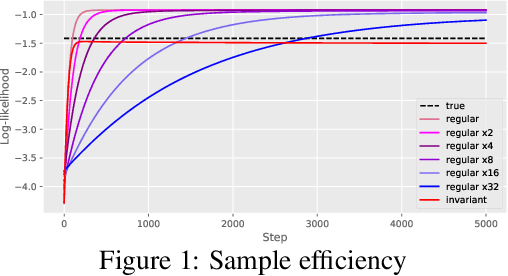
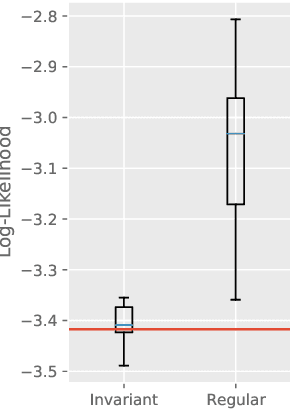
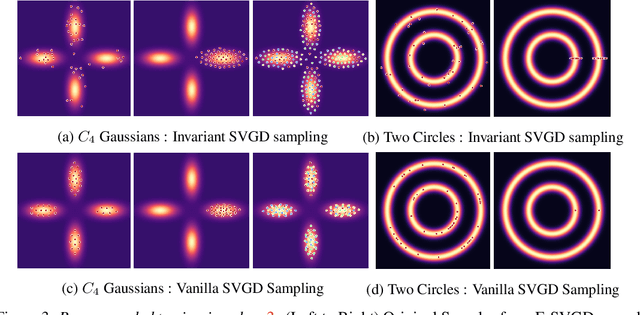
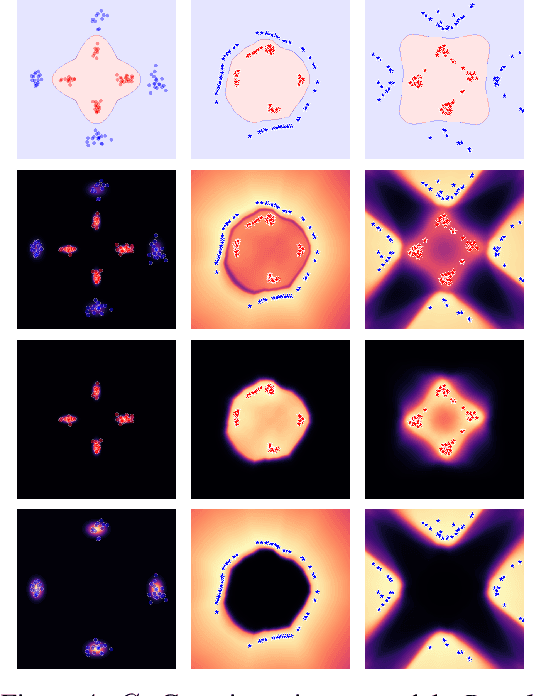
Learning Equivariant Energy Based Models with Equivariant Stein Variational Gradient Descent

We focus on the problem of efficient sampling and learning of probability densities by incorporating symmetries in probabilistic models. We first introduce Equivariant Stein Variational Gradient Descent algorithm -- an equivariant sampling method based on Stein's identity for sampling from densities with symmetries. Equivariant SVGD explicitly incorporates symmetry information in a density through equivariant kernels which makes the resultant sampler efficient both in terms of sample complexity and the quality of generated samples. Subsequently, we define equivariant energy based models to model invariant densities that are learned using contrastive divergence. By utilizing our equivariant SVGD for training equivariant EBMs, we propose new ways of improving and scaling up training of energy based models. We apply these equivariant energy models for modelling joint densities in regression and classification tasks for image datasets, many-body particle systems and molecular structure generation.

Robustness of Generalized Learning Vector Quantization Models against Adversarial Attacks

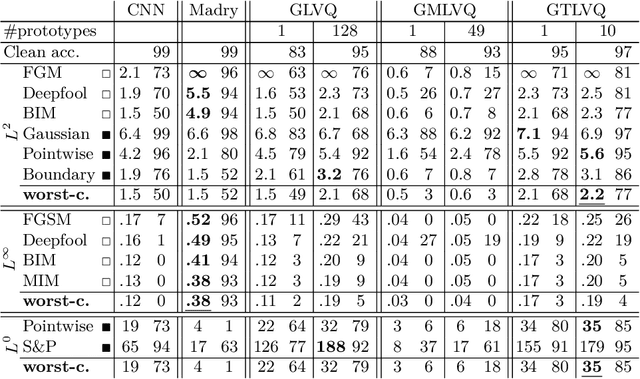
Adversarial attacks and the development of (deep) neural networks robust against them are currently two widely researched topics. The robustness of Learning Vector Quantization (LVQ) models against adversarial attacks has however not yet been studied to the same extent. We therefore present an extensive evaluation of three LVQ models: Generalized LVQ, Generalized Matrix LVQ and Generalized Tangent LVQ. The evaluation suggests that both Generalized LVQ and Generalized Tangent LVQ have a high base robustness, on par with the current state-of-the-art in robust neural network methods. In contrast to this, Generalized Matrix LVQ shows a high susceptibility to adversarial attacks, scoring consistently behind all other models. Additionally, our numerical evaluation indicates that increasing the number of prototypes per class improves the robustness of the models.

Prototype-based Neural Network Layers: Incorporating Vector Quantization

Neural networks currently dominate the machine learning community and they do so for good reasons. Their accuracy on complex tasks such as image classification is unrivaled at the moment and with recent improvements they are reasonably easy to train. Nevertheless, neural networks are lacking robustness and interpretability. Prototype-based vector quantization methods on the other hand are known for being robust and interpretable. For this reason, we propose techniques and strategies to merge both approaches. This contribution will particularly highlight the similarities between them and outline how to construct a prototype-based classification layer for multilayer networks. Additionally, we provide an alternative, prototype-based, approach to the classical convolution operation. Numerical results are not part of this report, instead the focus lays on establishing a strong theoretical framework. By publishing our framework and the respective theoretical considerations and justifications before finalizing our numerical experiments we hope to jump-start the incorporation of prototype-based learning in neural networks and vice versa.