Ferry Hooft
Path Integral Stochastic Optimal Control for Sampling Transition Paths
Jun 27, 2022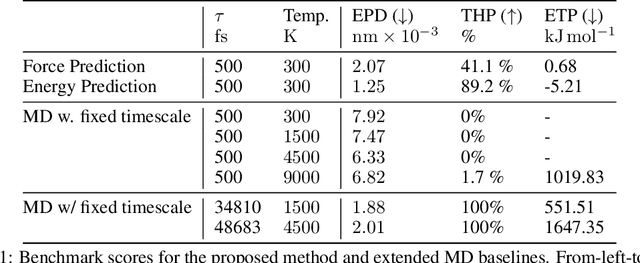
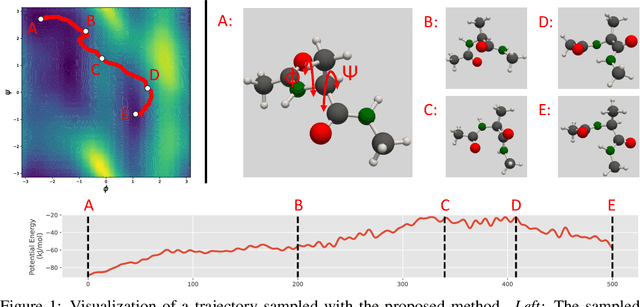
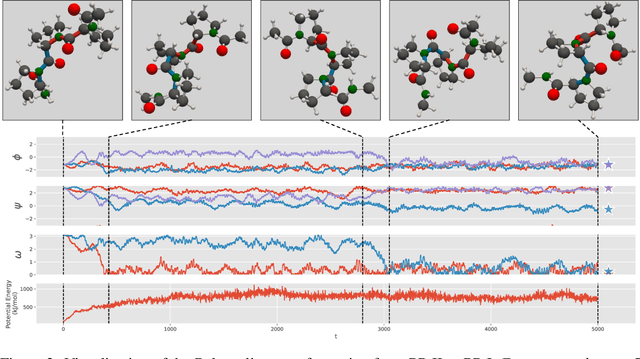
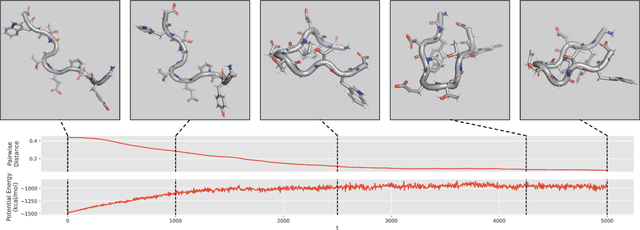
Abstract:We consider the problem of Sampling Transition Paths. Given two metastable conformational states of a molecular system, eg. a folded and unfolded protein, we aim to sample the most likely transition path between the two states. Sampling such a transition path is computationally expensive due to the existence of high free energy barriers between the two states. To circumvent this, previous work has focused on simplifying the trajectories to occur along specific molecular descriptors called Collective Variables (CVs). However, finding CVs is not trivial and requires chemical intuition. For larger molecules, where intuition is not sufficient, using these CV-based methods biases the transition along possibly irrelevant dimensions. Instead, this work proposes a method for sampling transition paths that consider the entire geometry of the molecules. To achieve this, we first relate the problem to recent work on the Schrodinger bridge problem and stochastic optimal control. Using this relation, we construct a method that takes into account important characteristics of molecular systems such as second-order dynamics and invariance to rotations and translations. We demonstrate our method on the commonly studied Alanine Dipeptide, but also consider larger proteins such as Polyproline and Chignolin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge