Takumi Kobayashi
Bi-LAT: Bilateral Control-Based Imitation Learning via Natural Language and Action Chunking with Transformers
Apr 02, 2025Abstract:We present Bi-LAT, a novel imitation learning framework that unifies bilateral control with natural language processing to achieve precise force modulation in robotic manipulation. Bi-LAT leverages joint position, velocity, and torque data from leader-follower teleoperation while also integrating visual and linguistic cues to dynamically adjust applied force. By encoding human instructions such as "softly grasp the cup" or "strongly twist the sponge" through a multimodal Transformer-based model, Bi-LAT learns to distinguish nuanced force requirements in real-world tasks. We demonstrate Bi-LAT's performance in (1) unimanual cup-stacking scenario where the robot accurately modulates grasp force based on language commands, and (2) bimanual sponge-twisting task that requires coordinated force control. Experimental results show that Bi-LAT effectively reproduces the instructed force levels, particularly when incorporating SigLIP among tested language encoders. Our findings demonstrate the potential of integrating natural language cues into imitation learning, paving the way for more intuitive and adaptive human-robot interaction. For additional material, please visit: https://mertcookimg.github.io/bi-lat/
Geometric Mean Improves Loss For Few-Shot Learning
Jan 24, 2025
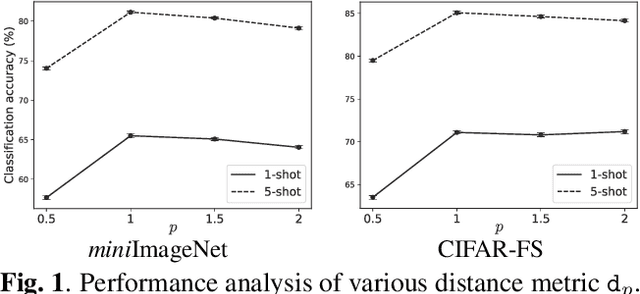
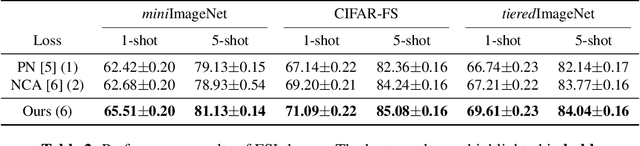
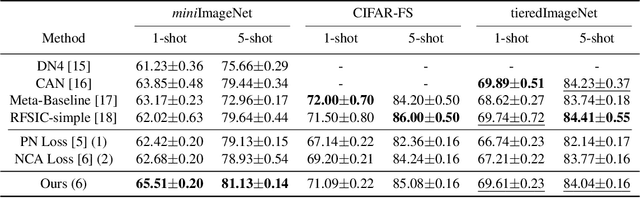
Abstract:Few-shot learning (FSL) is a challenging task in machine learning, demanding a model to render discriminative classification by using only a few labeled samples. In the literature of FSL, deep models are trained in a manner of metric learning to provide metric in a feature space which is well generalizable to classify samples of novel classes; in the space, even a few amount of labeled training examples can construct an effective classifier. In this paper, we propose a novel FSL loss based on \emph{geometric mean} to embed discriminative metric into deep features. In contrast to the other losses such as utilizing arithmetic mean in softmax-based formulation, the proposed method leverages geometric mean to aggregate pair-wise relationships among samples for enhancing discriminative metric across class categories. The proposed loss is not only formulated in a simple form but also is thoroughly analyzed in theoretical ways to reveal its favorable characteristics which are favorable for learning feature metric in FSL. In the experiments on few-shot image classification tasks, the method produces competitive performance in comparison to the other losses.
ALPHA-$α$ and Bi-ACT Are All You Need: Importance of Position and Force Information/Control for Imitation Learning of Unimanual and Bimanual Robotic Manipulation with Low-Cost System
Nov 15, 2024

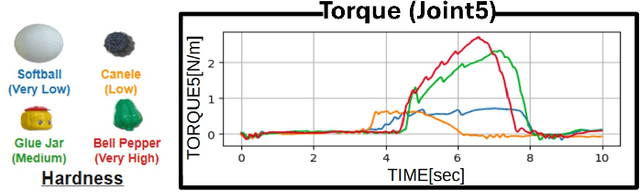
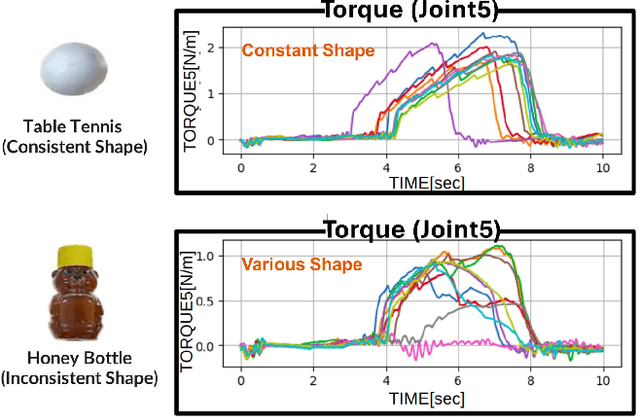
Abstract:Autonomous manipulation in everyday tasks requires flexible action generation to handle complex, diverse real-world environments, such as objects with varying hardness and softness. Imitation Learning (IL) enables robots to learn complex tasks from expert demonstrations. However, a lot of existing methods rely on position/unilateral control, leaving challenges in tasks that require force information/control, like carefully grasping fragile or varying-hardness objects. As the need for diverse controls increases, there are demand for low-cost bimanual robots that consider various motor inputs. To address these challenges, we introduce Bilateral Control-Based Imitation Learning via Action Chunking with Transformers(Bi-ACT) and"A" "L"ow-cost "P"hysical "Ha"rdware Considering Diverse Motor Control Modes for Research in Everyday Bimanual Robotic Manipulation (ALPHA-$\alpha$). Bi-ACT leverages bilateral control to utilize both position and force information, enhancing the robot's adaptability to object characteristics such as hardness, shape, and weight. The concept of ALPHA-$\alpha$ is affordability, ease of use, repairability, ease of assembly, and diverse control modes (position, velocity, torque), allowing researchers/developers to freely build control systems using ALPHA-$\alpha$. In our experiments, we conducted a detailed analysis of Bi-ACT in unimanual manipulation tasks, confirming its superior performance and adaptability compared to Bi-ACT without force control. Based on these results, we applied Bi-ACT to bimanual manipulation tasks. Experimental results demonstrated high success rates in coordinated bimanual operations across multiple tasks. The effectiveness of the Bi-ACT and ALPHA-$\alpha$ can be seen through comprehensive real-world experiments. Video available at: https://mertcookimg.github.io/alpha-biact/
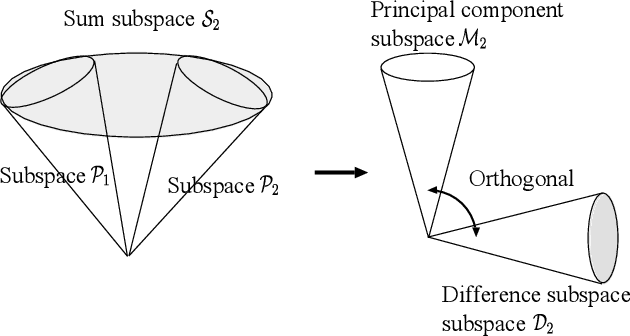
Second-order difference subspace
Sep 13, 2024Abstract:Subspace representation is a fundamental technique in various fields of machine learning. Analyzing a geometrical relationship among multiple subspaces is essential for understanding subspace series' temporal and/or spatial dynamics. This paper proposes the second-order difference subspace, a higher-order extension of the first-order difference subspace between two subspaces that can analyze the geometrical difference between them. As a preliminary for that, we extend the definition of the first-order difference subspace to the more general setting that two subspaces with different dimensions have an intersection. We then define the second-order difference subspace by combining the concept of first-order difference subspace and principal component subspace (Karcher mean) between two subspaces, motivated by the second-order central difference method. We can understand that the first/second-order difference subspaces correspond to the velocity and acceleration of subspace dynamics from the viewpoint of a geodesic on a Grassmann manifold. We demonstrate the validity and naturalness of our second-order difference subspace by showing numerical results on two applications: temporal shape analysis of a 3D object and time series analysis of a biometric signal.
Grassmannian learning mutual subspace method for image set recognition
Nov 08, 2021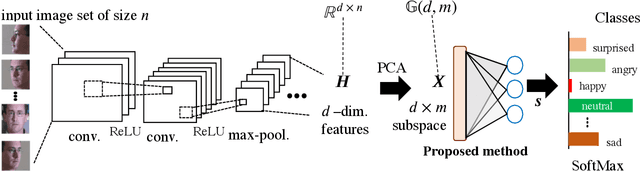
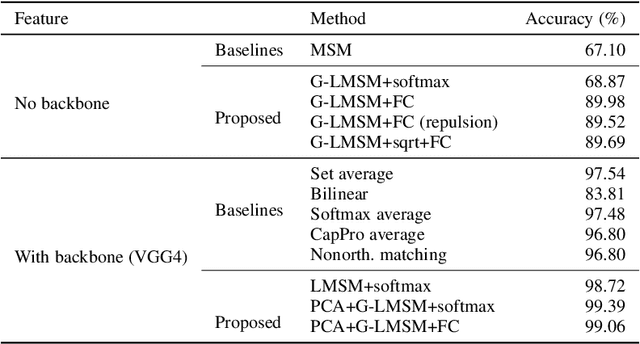
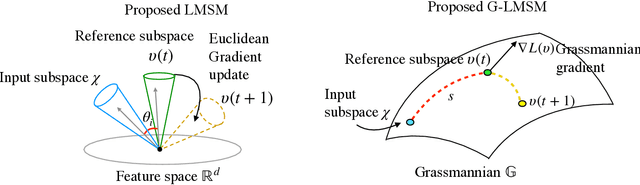
Abstract:This paper addresses the problem of object recognition given a set of images as input (e.g., multiple camera sources and video frames). Convolutional neural network (CNN)-based frameworks do not exploit these sets effectively, processing a pattern as observed, not capturing the underlying feature distribution as it does not consider the variance of images in the set. To address this issue, we propose the Grassmannian learning mutual subspace method (G-LMSM), a NN layer embedded on top of CNNs as a classifier, that can process image sets more effectively and can be trained in an end-to-end manner. The image set is represented by a low-dimensional input subspace; and this input subspace is matched with reference subspaces by a similarity of their canonical angles, an interpretable and easy to compute metric. The key idea of G-LMSM is that the reference subspaces are learned as points on the Grassmann manifold, optimized with Riemannian stochastic gradient descent. This learning is stable, efficient and theoretically well-grounded. We demonstrate the effectiveness of our proposed method on hand shape recognition, face identification, and facial emotion recognition.
Discriminant analysis based on projection onto generalized difference subspace
Oct 30, 2019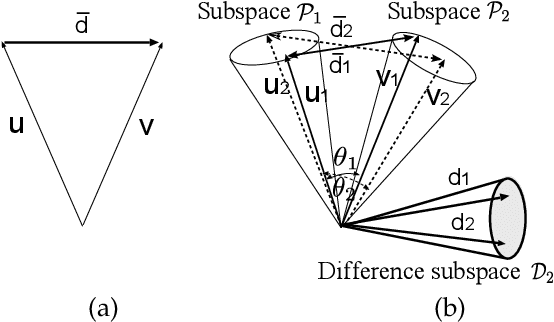

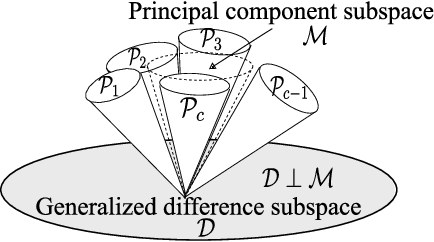
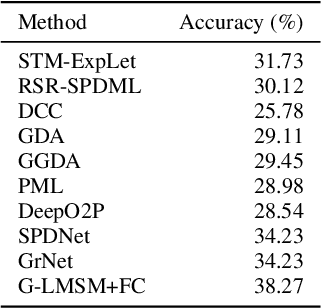
Abstract:This paper discusses a new type of discriminant analysis based on the orthogonal projection of data onto a generalized difference subspace (GDS). In our previous work, we have demonstrated that GDS projection works as the quasi-orthogonalization of class subspaces, which is an effective feature extraction for subspace based classifiers. Interestingly, GDS projection also works as a discriminant feature extraction through a similar mechanism to the Fisher discriminant analysis (FDA). A direct proof of the connection between GDS projection and FDA is difficult due to the significant difference in their formulations. To avoid the difficulty, we first introduce geometrical Fisher discriminant analysis (gFDA) based on a simplified Fisher criterion. Our simplified Fisher criterion is derived from a heuristic yet practically plausible principle: the direction of the sample mean vector of a class is in most cases almost equal to that of the first principal component vector of the class, under the condition that the principal component vectors are calculated by applying the principal component analysis (PCA) without data centering. gFDA can work stably even under few samples, bypassing the small sample size (SSS) problem of FDA. Next, we prove that gFDA is equivalent to GDS projection with a small correction term. This equivalence ensures GDS projection to inherit the discriminant ability from FDA via gFDA. Furthermore, to enhance the performances of gFDA and GDS projection, we normalize the projected vectors on the discriminant spaces. Extensive experiments using the extended Yale B+ database and the CMU face database show that gFDA and GDS projection have equivalent or better performance than the original FDA and its extensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge