Discriminant analysis based on projection onto generalized difference subspace

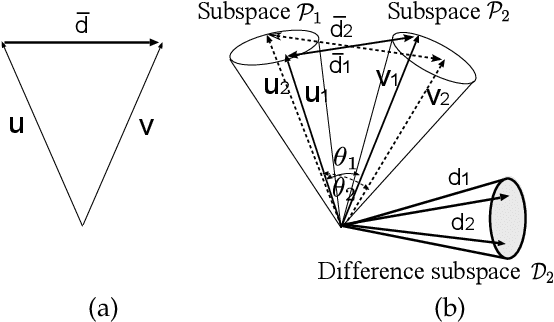
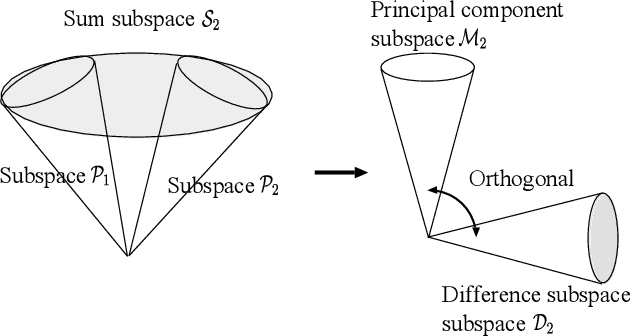
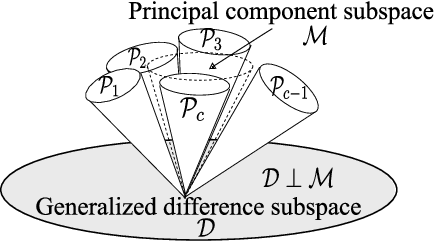
This paper discusses a new type of discriminant analysis based on the orthogonal projection of data onto a generalized difference subspace (GDS). In our previous work, we have demonstrated that GDS projection works as the quasi-orthogonalization of class subspaces, which is an effective feature extraction for subspace based classifiers. Interestingly, GDS projection also works as a discriminant feature extraction through a similar mechanism to the Fisher discriminant analysis (FDA). A direct proof of the connection between GDS projection and FDA is difficult due to the significant difference in their formulations. To avoid the difficulty, we first introduce geometrical Fisher discriminant analysis (gFDA) based on a simplified Fisher criterion. Our simplified Fisher criterion is derived from a heuristic yet practically plausible principle: the direction of the sample mean vector of a class is in most cases almost equal to that of the first principal component vector of the class, under the condition that the principal component vectors are calculated by applying the principal component analysis (PCA) without data centering. gFDA can work stably even under few samples, bypassing the small sample size (SSS) problem of FDA. Next, we prove that gFDA is equivalent to GDS projection with a small correction term. This equivalence ensures GDS projection to inherit the discriminant ability from FDA via gFDA. Furthermore, to enhance the performances of gFDA and GDS projection, we normalize the projected vectors on the discriminant spaces. Extensive experiments using the extended Yale B+ database and the CMU face database show that gFDA and GDS projection have equivalent or better performance than the original FDA and its extensions.