SED2AM: Solving Multi-Trip Time-Dependent Vehicle Routing Problem using Deep Reinforcement Learning

Deep reinforcement learning (DRL)-based frameworks, featuring Transformer-style policy networks, have demonstrated their efficacy across various vehicle routing problem (VRP) variants. However, the application of these methods to the multi-trip time-dependent vehicle routing problem (MTTDVRP) with maximum working hours constraints -- a pivotal element of urban logistics -- remains largely unexplored. This paper introduces a DRL-based method called the Simultaneous Encoder and Dual Decoder Attention Model (SED2AM), tailored for the MTTDVRP with maximum working hours constraints. The proposed method introduces a temporal locality inductive bias to the encoding module of the policy networks, enabling it to effectively account for the time-dependency in travel distance or time. The decoding module of SED2AM includes a vehicle selection decoder that selects a vehicle from the fleet, effectively associating trips with vehicles for functional multi-trip routing. Additionally, this decoding module is equipped with a trip construction decoder leveraged for constructing trips for the vehicles. This policy model is equipped with two classes of state representations, fleet state and routing state, providing the information needed for effective route construction in the presence of maximum working hours constraints. Experimental results using real-world datasets from two major Canadian cities not only show that SED2AM outperforms the current state-of-the-art DRL-based and metaheuristic-based baselines but also demonstrate its generalizability to solve larger-scale problems.

OBELiX: A Curated Dataset of Crystal Structures and Experimentally Measured Ionic Conductivities for Lithium Solid-State Electrolytes

Solid-state electrolyte batteries are expected to replace liquid electrolyte lithium-ion batteries in the near future thanks to their higher theoretical energy density and improved safety. However, their adoption is currently hindered by their lower effective ionic conductivity, a quantity that governs charge and discharge rates. Identifying highly ion-conductive materials using conventional theoretical calculations and experimental validation is both time-consuming and resource-intensive. While machine learning holds the promise to expedite this process, relevant ionic conductivity and structural data is scarce. Here, we present OBELiX, a domain-expert-curated database of $\sim$600 synthesized solid electrolyte materials and their experimentally measured room temperature ionic conductivities gathered from literature. Each material is described by their measured composition, space group and lattice parameters. A full-crystal description in the form of a crystallographic information file (CIF) is provided for ~320 structures for which atomic positions were available. We discuss various statistics and features of the dataset and provide training and testing splits that avoid data leakage. Finally, we benchmark seven existing ML models on the task of predicting ionic conductivity and discuss their performance. The goal of this work is to facilitate the use of machine learning for solid-state electrolyte materials discovery.

$f$-MICL: Understanding and Generalizing InfoNCE-based Contrastive Learning

In self-supervised contrastive learning, a widely-adopted objective function is InfoNCE, which uses the heuristic cosine similarity for the representation comparison, and is closely related to maximizing the Kullback-Leibler (KL)-based mutual information. In this paper, we aim at answering two intriguing questions: (1) Can we go beyond the KL-based objective? (2) Besides the popular cosine similarity, can we design a better similarity function? We provide answers to both questions by generalizing the KL-based mutual information to the $f$-Mutual Information in Contrastive Learning ($f$-MICL) using the $f$-divergences. To answer the first question, we provide a wide range of $f$-MICL objectives which share the nice properties of InfoNCE (e.g., alignment and uniformity), and meanwhile result in similar or even superior performance. For the second question, assuming that the joint feature distribution is proportional to the Gaussian kernel, we derive an $f$-Gaussian similarity with better interpretability and empirical performance. Finally, we identify close relationships between the $f$-MICL objective and several popular InfoNCE-based objectives. Using benchmark tasks from both vision and natural language, we empirically evaluate $f$-MICL with different $f$-divergences on various architectures (SimCLR, MoCo, and MoCo v3) and datasets. We observe that $f$-MICL generally outperforms the benchmarks and the best-performing $f$-divergence is task and dataset dependent.

SoftEdge: Regularizing Graph Classification with Random Soft Edges

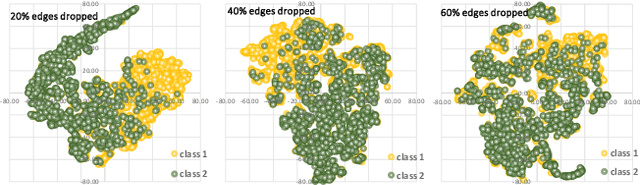
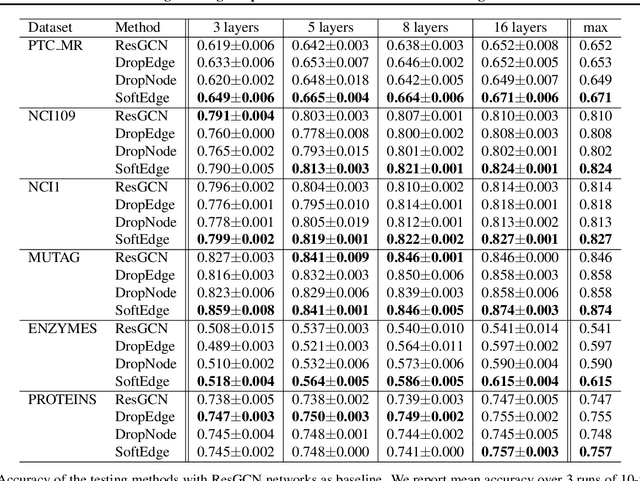
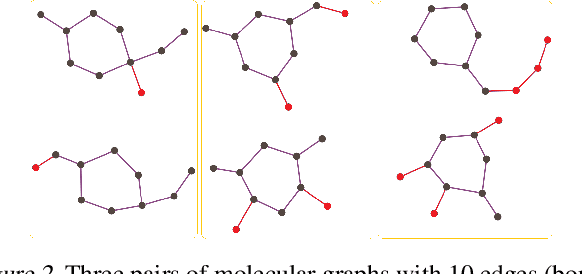
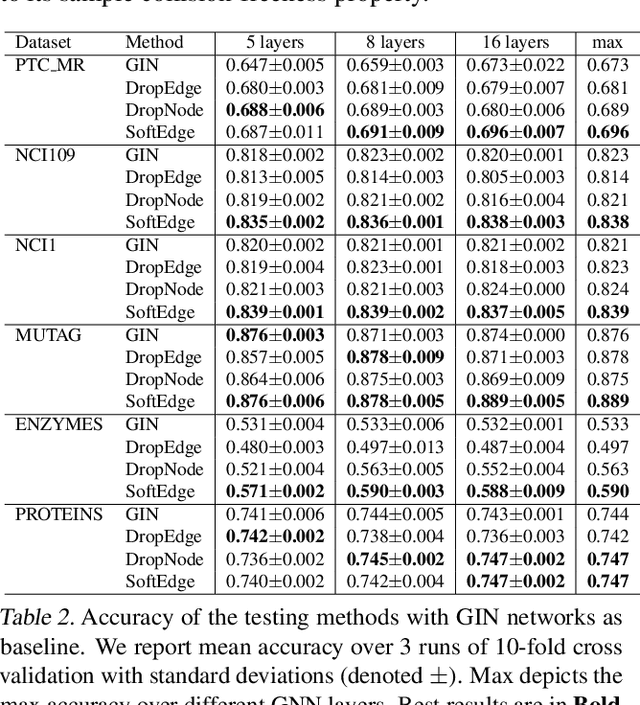
Graph data augmentation plays a vital role in regularizing Graph Neural Networks (GNNs), which leverage information exchange along edges in graphs, in the form of message passing, for learning. Due to their effectiveness, simple edge and node manipulations (e.g., addition and deletion) have been widely used in graph augmentation. In this paper, we identify a limitation in such a common augmentation technique. That is, simple edge and node manipulations can create graphs with an identical structure or indistinguishable structures to message passing GNNs but of conflict labels, leading to the sample collision issue and thus the degradation of model performance. To address this problem, we propose SoftEdge, which assigns random weights to a portion of the edges of a given graph to construct dynamic neighborhoods over the graph. We prove that SoftEdge creates collision-free augmented graphs. We also show that this simple method obtains superior accuracy to popular node and edge manipulation approaches and notable resilience to the accuracy degradation with the GNN depth.

Symmetric Wasserstein Autoencoders

Leveraging the framework of Optimal Transport, we introduce a new family of generative autoencoders with a learnable prior, called Symmetric Wasserstein Autoencoders (SWAEs). We propose to symmetrically match the joint distributions of the observed data and the latent representation induced by the encoder and the decoder. The resulting algorithm jointly optimizes the modelling losses in both the data and the latent spaces with the loss in the data space leading to the denoising effect. With the symmetric treatment of the data and the latent representation, the algorithm implicitly preserves the local structure of the data in the latent space. To further improve the quality of the latent representation, we incorporate a reconstruction loss into the objective, which significantly benefits both the generation and reconstruction. We empirically show the superior performance of SWAEs over the state-of-the-art generative autoencoders in terms of classification, reconstruction, and generation.