SIReN-VAE: Leveraging Flows and Amortized Inference for Bayesian Networks

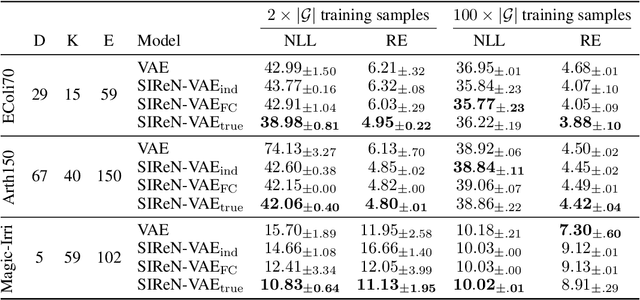
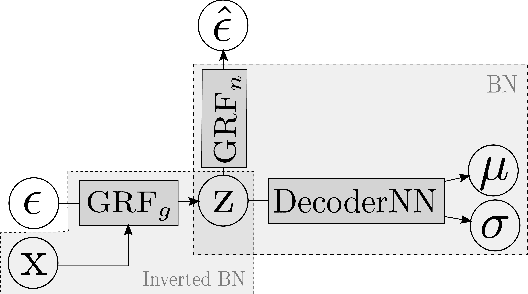
Initial work on variational autoencoders assumed independent latent variables with simple distributions. Subsequent work has explored incorporating more complex distributions and dependency structures: including normalizing flows in the encoder network allows latent variables to entangle non-linearly, creating a richer class of distributions for the approximate posterior, and stacking layers of latent variables allows more complex priors to be specified for the generative model. This work explores incorporating arbitrary dependency structures, as specified by Bayesian networks, into VAEs. This is achieved by extending both the prior and inference network with graphical residual flows - residual flows that encode conditional independence by masking the weight matrices of the flow's residual blocks. We compare our model's performance on several synthetic datasets and show its potential in data-sparse settings.

Graphical Residual Flows

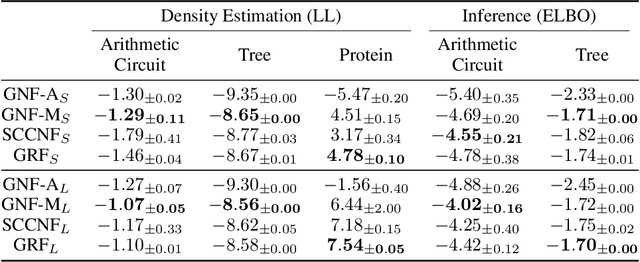
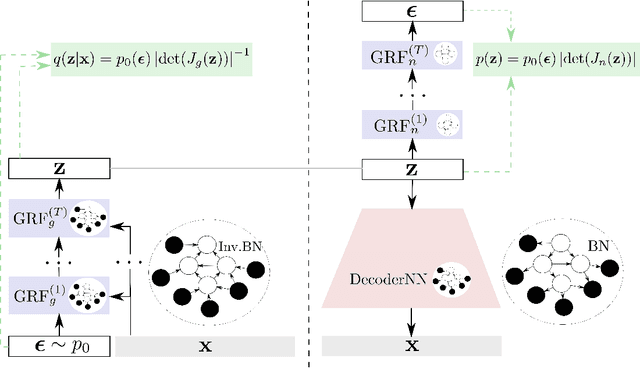
Graphical flows add further structure to normalizing flows by encoding non-trivial variable dependencies. Previous graphical flow models have focused primarily on a single flow direction: the normalizing direction for density estimation, or the generative direction for inference. However, to use a single flow to perform tasks in both directions, the model must exhibit stable and efficient flow inversion. This work introduces graphical residual flows, a graphical flow based on invertible residual networks. Our approach to incorporating dependency information in the flow, means that we are able to calculate the Jacobian determinant of these flows exactly. Our experiments confirm that graphical residual flows provide stable and accurate inversion that is also more time-efficient than alternative flows with similar task performance. Furthermore, our model provides performance competitive with other graphical flows for both density estimation and inference tasks.

Performance-Agnostic Fusion of Probabilistic Classifier Outputs

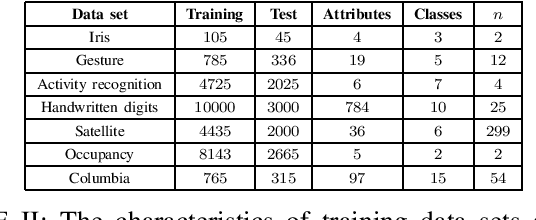
We propose a method for combining probabilistic outputs of classifiers to make a single consensus class prediction when no further information about the individual classifiers is available, beyond that they have been trained for the same task. The lack of relevant prior information rules out typical applications of Bayesian or Dempster-Shafer methods, and the default approach here would be methods based on the principle of indifference, such as the sum or product rule, which essentially weight all classifiers equally. In contrast, our approach considers the diversity between the outputs of the various classifiers, iteratively updating predictions based on their correspondence with other predictions until the predictions converge to a consensus decision. The intuition behind this approach is that classifiers trained for the same task should typically exhibit regularities in their outputs on a new task; the predictions of classifiers which differ significantly from those of others are thus given less credence using our approach. The approach implicitly assumes a symmetric loss function, in that the relative cost of various prediction errors are not taken into account. Performance of the model is demonstrated on different benchmark datasets. Our proposed method works well in situations where accuracy is the performance metric; however, it does not output calibrated probabilities, so it is not suitable in situations where such probabilities are required for further processing.

Stochastic Gradient Annealed Importance Sampling for Efficient Online Marginal Likelihood Estimation

We consider estimating the marginal likelihood in settings with independent and identically distributed (i.i.d.) data. We propose estimating the predictive distributions in a sequential factorization of the marginal likelihood in such settings by using stochastic gradient Markov Chain Monte Carlo techniques. This approach is far more efficient than traditional marginal likelihood estimation techniques such as nested sampling and annealed importance sampling due to its use of mini-batches to approximate the likelihood. Stability of the estimates is provided by an adaptive annealing schedule. The resulting stochastic gradient annealed importance sampling (SGAIS) technique, which is the key contribution of our paper, enables us to estimate the marginal likelihood of a number of models considerably faster than traditional approaches, with no noticeable loss of accuracy. An important benefit of our approach is that the marginal likelihood is calculated in an online fashion as data becomes available, allowing the estimates to be used for applications such as online weighted model combination.

Stabilising priors for robust Bayesian deep learning

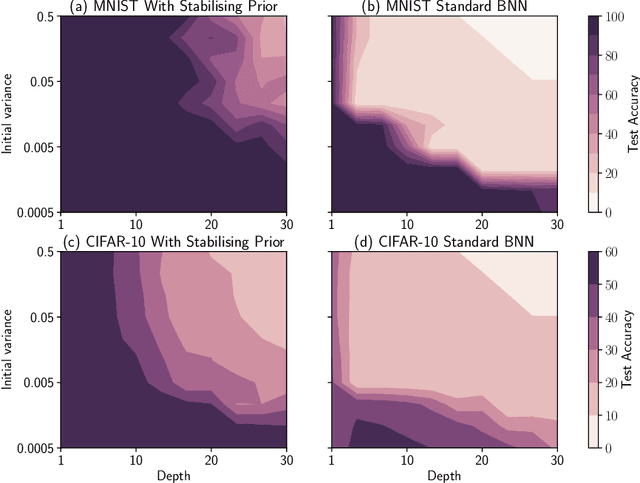
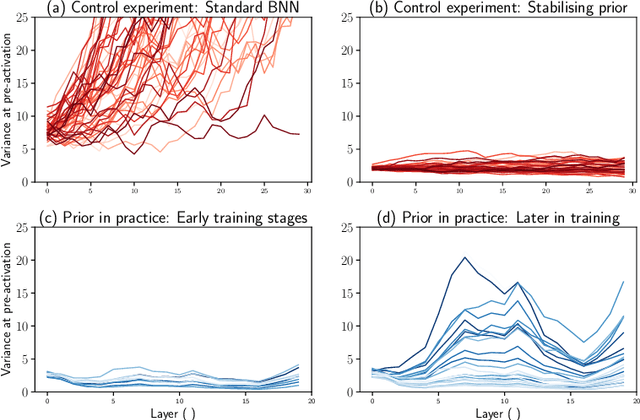
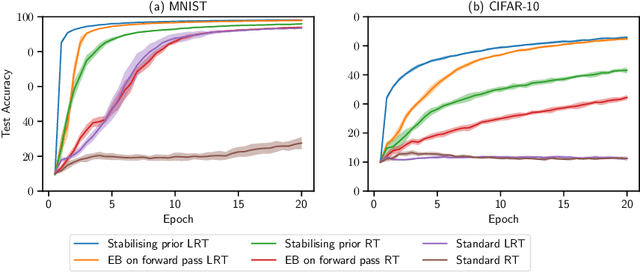
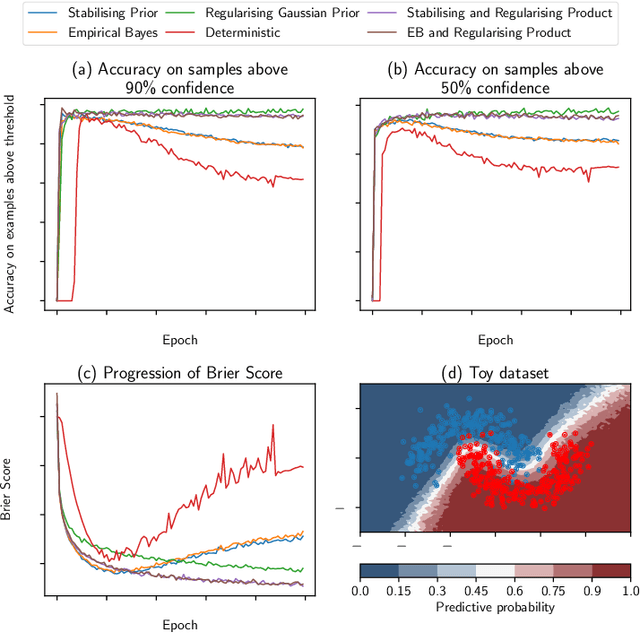
Bayesian neural networks (BNNs) have developed into useful tools for probabilistic modelling due to recent advances in variational inference enabling large scale BNNs. However, BNNs remain brittle and hard to train, especially: (1) when using deep architectures consisting of many hidden layers and (2) in situations with large weight variances. We use signal propagation theory to quantify these challenges and propose self-stabilising priors. This is achieved by a reformulation of the ELBO to allow the prior to influence network signal propagation. Then, we develop a stabilising prior, where the distributional parameters of the prior are adjusted before each forward pass to ensure stability of the propagating signal. This stabilised signal propagation leads to improved convergence and robustness making it possible to train deeper networks and in more noisy settings.

If dropout limits trainable depth, does critical initialisation still matter? A large-scale statistical analysis on ReLU networks

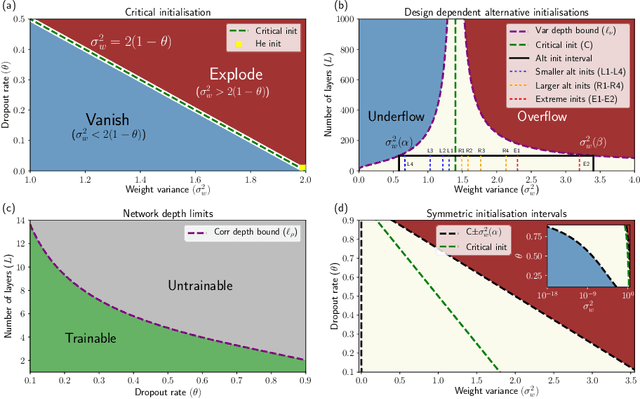
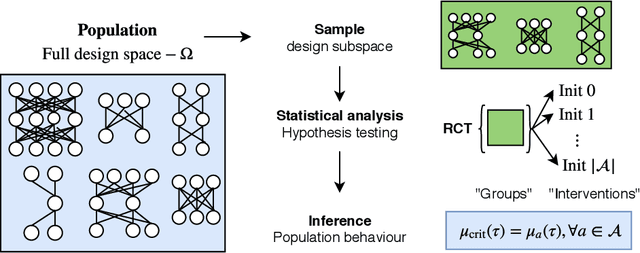
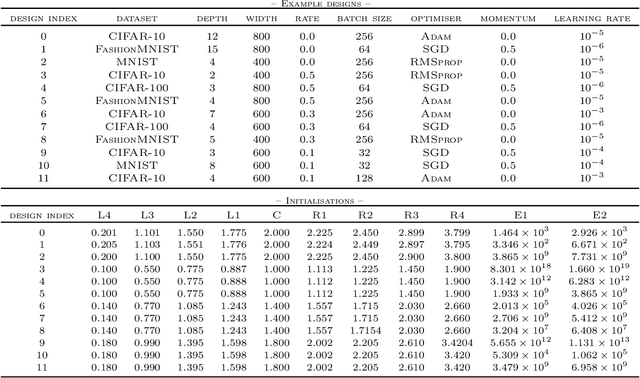
Recent work in signal propagation theory has shown that dropout limits the depth to which information can propagate through a neural network. In this paper, we investigate the effect of initialisation on training speed and generalisation for ReLU networks within this depth limit. We ask the following research question: given that critical initialisation is crucial for training at large depth, if dropout limits the depth at which networks are trainable, does initialising critically still matter? We conduct a large-scale controlled experiment, and perform a statistical analysis of over $12000$ trained networks. We find that (1) trainable networks show no statistically significant difference in performance over a wide range of non-critical initialisations; (2) for initialisations that show a statistically significant difference, the net effect on performance is small; (3) only extreme initialisations (very small or very large) perform worse than criticality. These findings also apply to standard ReLU networks of moderate depth as a special case of zero dropout. Our results therefore suggest that, in the shallow-to-moderate depth setting, critical initialisation provides zero performance gains when compared to off-critical initialisations and that searching for off-critical initialisations that might improve training speed or generalisation, is likely to be a fruitless endeavour.

On the expected behaviour of noise regularised deep neural networks as Gaussian processes

Recent work has established the equivalence between deep neural networks and Gaussian processes (GPs), resulting in so-called neural network Gaussian processes (NNGPs). The behaviour of these models depends on the initialisation of the corresponding network. In this work, we consider the impact of noise regularisation (e.g. dropout) on NNGPs, and relate their behaviour to signal propagation theory in noise regularised deep neural networks. For ReLU activations, we find that the best performing NNGPs have kernel parameters that correspond to a recently proposed initialisation scheme for noise regularised ReLU networks. In addition, we show how the noise influences the covariance matrix of the NNGP, producing a stronger prior towards simple functions away from the training points. We verify our theoretical findings with experiments on MNIST and CIFAR-10 as well as on synthetic data.

A Coordinated Search Strategy for Multiple Solitary Robots: An Extension

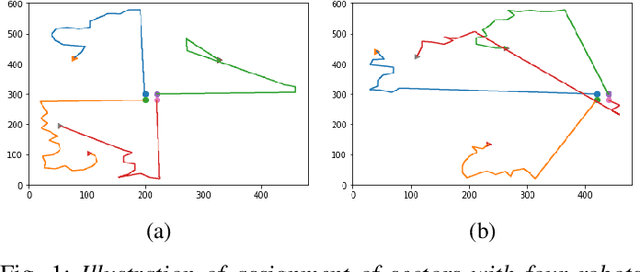
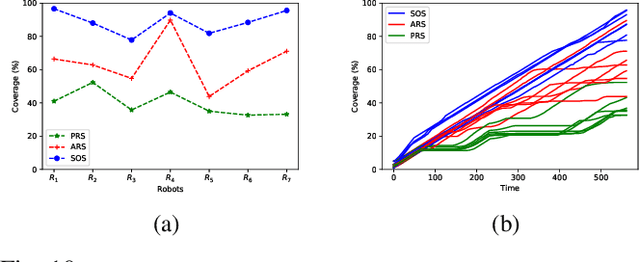
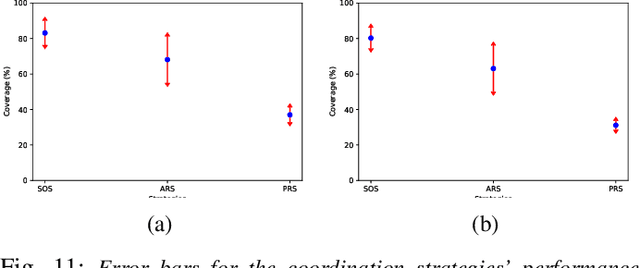
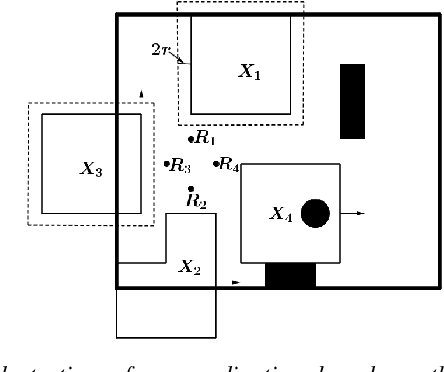
The problem of coordination without a priori information about the environment is important in robotics. Applications vary from formation control to search and rescue. This paper considers the problem of search by a group of solitary robots: self-interested robots without a priori knowledge about each other, and with restricted communication capacity. When the capacity of robots to communicate is limited, they may obliviously search in overlapping regions (i.e. be subject to interference). Interference hinders robot progress, and strategies have been proposed in the literature to mitigate interference [1], [2]. Interaction of solitary robots has attracted much interest in robotics, but the problem of mitigating interference when time for search is limited remains an important area of research. We propose a coordination strategy based on the method of cellular decomposition [3] where we employ the concept of soft obstacles: a robot considers cells assigned to other robots as obstacles. The performance of the proposed strategy is demonstrated by means of simulation experiments. Simulations indicate the utility of the strategy in situations where a known upper bound on the search time precludes search of the entire environment.

Critical initialisation for deep signal propagation in noisy rectifier neural networks

Stochastic regularisation is an important weapon in the arsenal of a deep learning practitioner. However, despite recent theoretical advances, our understanding of how noise influences signal propagation in deep neural networks remains limited. By extending recent work based on mean field theory, we develop a new framework for signal propagation in stochastic regularised neural networks. Our noisy signal propagation theory can incorporate several common noise distributions, including additive and multiplicative Gaussian noise as well as dropout. We use this framework to investigate initialisation strategies for noisy ReLU networks. We show that no critical initialisation strategy exists using additive noise, with signal propagation exploding regardless of the selected noise distribution. For multiplicative noise (e.g. dropout), we identify alternative critical initialisation strategies that depend on the second moment of the noise distribution. Simulations and experiments on real-world data confirm that our proposed initialisation is able to stably propagate signals in deep networks, while using an initialisation disregarding noise fails to do so. Furthermore, we analyse correlation dynamics between inputs. Stronger noise regularisation is shown to reduce the depth to which discriminatory information about the inputs to a noisy ReLU network is able to propagate, even when initialised at criticality. We support our theoretical predictions for these trainable depths with simulations, as well as with experiments on MNIST and CIFAR-10

Learning Dynamics of Linear Denoising Autoencoders

Denoising autoencoders (DAEs) have proven useful for unsupervised representation learning, but a thorough theoretical understanding is still lacking of how the input noise influences learning. Here we develop theory for how noise influences learning in DAEs. By focusing on linear DAEs, we are able to derive analytic expressions that exactly describe their learning dynamics. We verify our theoretical predictions with simulations as well as experiments on MNIST and CIFAR-10. The theory illustrates how, when tuned correctly, noise allows DAEs to ignore low variance directions in the inputs while learning to reconstruct them. Furthermore, in a comparison of the learning dynamics of DAEs to standard regularised autoencoders, we show that noise has a similar regularisation effect to weight decay, but with faster training dynamics. We also show that our theoretical predictions approximate learning dynamics on real-world data and qualitatively match observed dynamics in nonlinear DAEs.