Performance-Agnostic Fusion of Probabilistic Classifier Outputs
Paper and Code
Sep 01, 2020

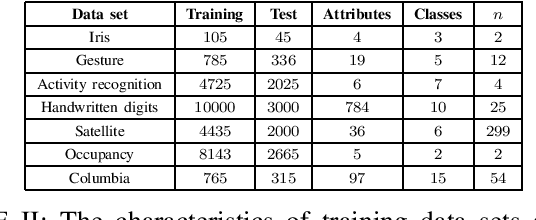
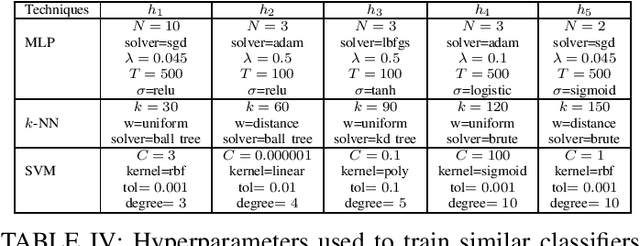
We propose a method for combining probabilistic outputs of classifiers to make a single consensus class prediction when no further information about the individual classifiers is available, beyond that they have been trained for the same task. The lack of relevant prior information rules out typical applications of Bayesian or Dempster-Shafer methods, and the default approach here would be methods based on the principle of indifference, such as the sum or product rule, which essentially weight all classifiers equally. In contrast, our approach considers the diversity between the outputs of the various classifiers, iteratively updating predictions based on their correspondence with other predictions until the predictions converge to a consensus decision. The intuition behind this approach is that classifiers trained for the same task should typically exhibit regularities in their outputs on a new task; the predictions of classifiers which differ significantly from those of others are thus given less credence using our approach. The approach implicitly assumes a symmetric loss function, in that the relative cost of various prediction errors are not taken into account. Performance of the model is demonstrated on different benchmark datasets. Our proposed method works well in situations where accuracy is the performance metric; however, it does not output calibrated probabilities, so it is not suitable in situations where such probabilities are required for further processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge