Stabilising priors for robust Bayesian deep learning
Paper and Code
Oct 23, 2019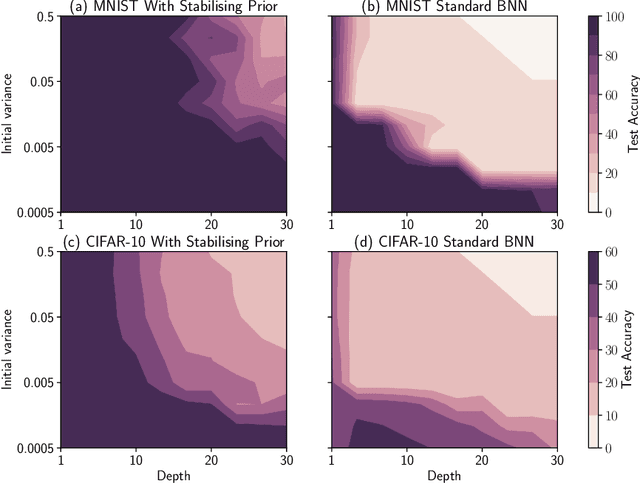
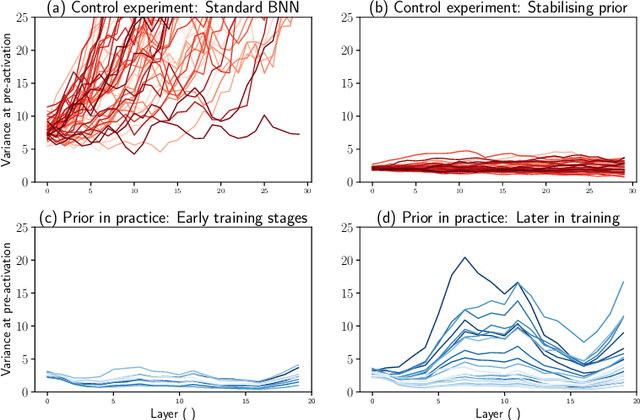
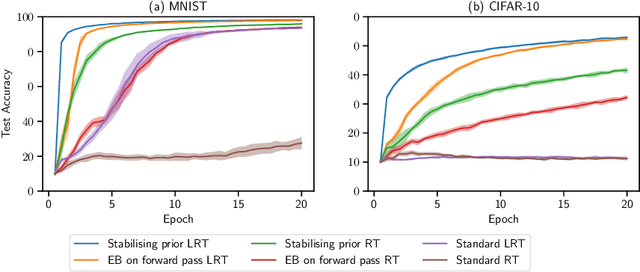
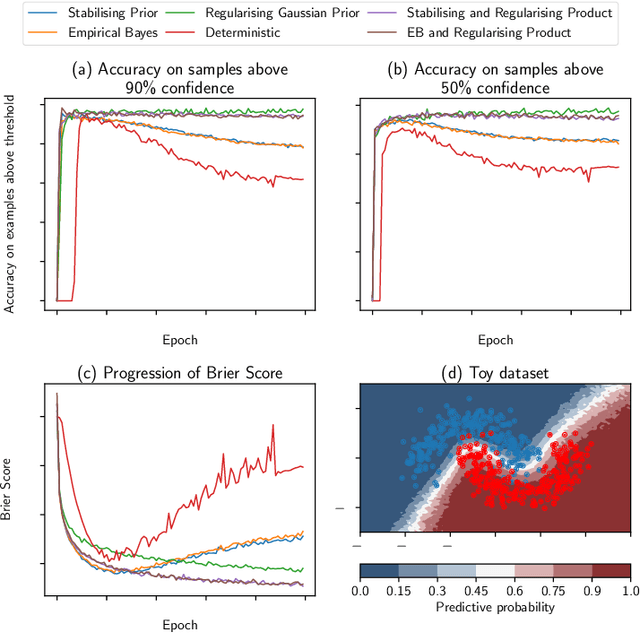
Bayesian neural networks (BNNs) have developed into useful tools for probabilistic modelling due to recent advances in variational inference enabling large scale BNNs. However, BNNs remain brittle and hard to train, especially: (1) when using deep architectures consisting of many hidden layers and (2) in situations with large weight variances. We use signal propagation theory to quantify these challenges and propose self-stabilising priors. This is achieved by a reformulation of the ELBO to allow the prior to influence network signal propagation. Then, we develop a stabilising prior, where the distributional parameters of the prior are adjusted before each forward pass to ensure stability of the propagating signal. This stabilised signal propagation leads to improved convergence and robustness making it possible to train deeper networks and in more noisy settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge