SIReN-VAE: Leveraging Flows and Amortized Inference for Bayesian Networks

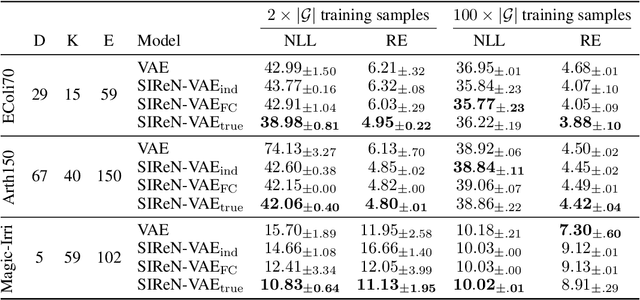
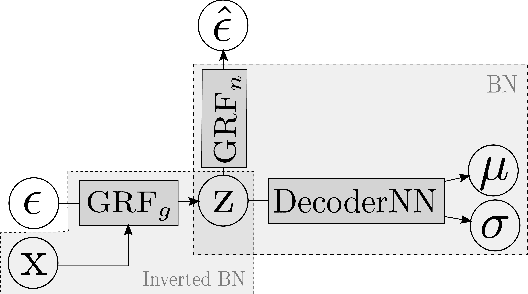
Initial work on variational autoencoders assumed independent latent variables with simple distributions. Subsequent work has explored incorporating more complex distributions and dependency structures: including normalizing flows in the encoder network allows latent variables to entangle non-linearly, creating a richer class of distributions for the approximate posterior, and stacking layers of latent variables allows more complex priors to be specified for the generative model. This work explores incorporating arbitrary dependency structures, as specified by Bayesian networks, into VAEs. This is achieved by extending both the prior and inference network with graphical residual flows - residual flows that encode conditional independence by masking the weight matrices of the flow's residual blocks. We compare our model's performance on several synthetic datasets and show its potential in data-sparse settings.

Graphical Residual Flows

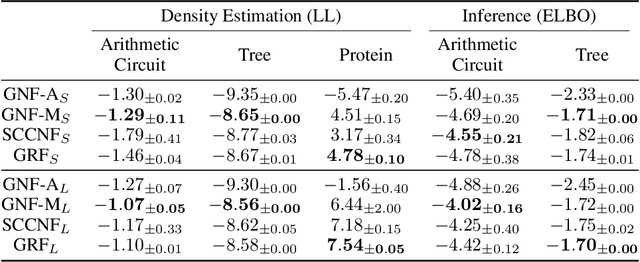
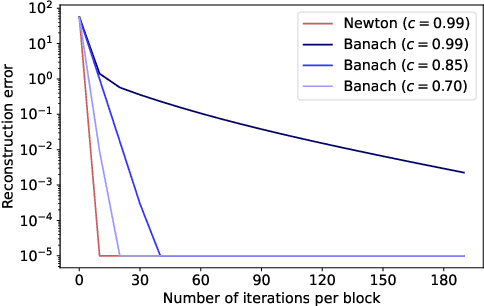
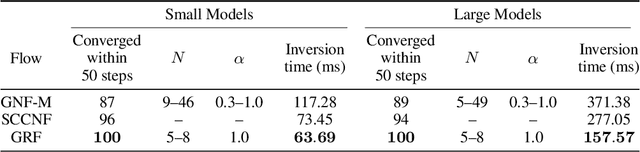
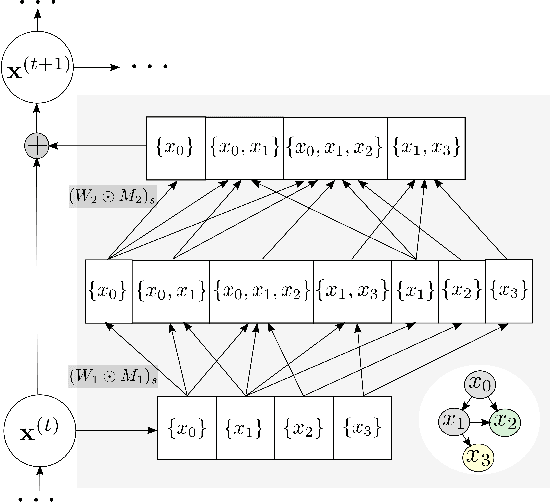
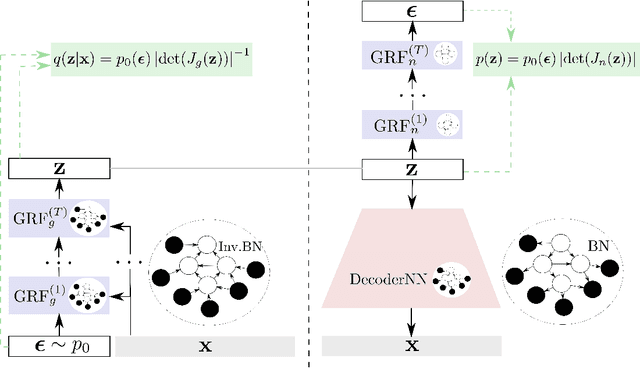
Graphical flows add further structure to normalizing flows by encoding non-trivial variable dependencies. Previous graphical flow models have focused primarily on a single flow direction: the normalizing direction for density estimation, or the generative direction for inference. However, to use a single flow to perform tasks in both directions, the model must exhibit stable and efficient flow inversion. This work introduces graphical residual flows, a graphical flow based on invertible residual networks. Our approach to incorporating dependency information in the flow, means that we are able to calculate the Jacobian determinant of these flows exactly. Our experiments confirm that graphical residual flows provide stable and accurate inversion that is also more time-efficient than alternative flows with similar task performance. Furthermore, our model provides performance competitive with other graphical flows for both density estimation and inference tasks.