Automated Discovery of Functional Actual Causes in Complex Environments

Reinforcement learning (RL) algorithms often struggle to learn policies that generalize to novel situations due to issues such as causal confusion, overfitting to irrelevant factors, and failure to isolate control of state factors. These issues stem from a common source: a failure to accurately identify and exploit state-specific causal relationships in the environment. While some prior works in RL aim to identify these relationships explicitly, they rely on informal domain-specific heuristics such as spatial and temporal proximity. Actual causality offers a principled and general framework for determining the causes of particular events. However, existing definitions of actual cause often attribute causality to a large number of events, even if many of them rarely influence the outcome. Prior work on actual causality proposes normality as a solution to this problem, but its existing implementations are challenging to scale to complex and continuous-valued RL environments. This paper introduces functional actual cause (FAC), a framework that uses context-specific independencies in the environment to restrict the set of actual causes. We additionally introduce Joint Optimization for Actual Cause Inference (JACI), an algorithm that learns from observational data to infer functional actual causes. We demonstrate empirically that FAC agrees with known results on a suite of examples from the actual causality literature, and JACI identifies actual causes with significantly higher accuracy than existing heuristic methods in a set of complex, continuous-valued environments.

SOPE: Spectrum of Off-Policy Estimators

Many sequential decision making problems are high-stakes and require off-policy evaluation (OPE) of a new policy using historical data collected using some other policy. One of the most common OPE techniques that provides unbiased estimates is trajectory based importance sampling (IS). However, due to the high variance of trajectory IS estimates, importance sampling methods based on state-action visitation distributions (SIS) have recently been adopted. Unfortunately, while SIS often provides lower variance estimates for long horizons, estimating the state-action distribution ratios can be challenging and lead to biased estimates. In this paper, we present a new perspective on this bias-variance trade-off and show the existence of a spectrum of estimators whose endpoints are SIS and IS. Additionally, we also establish a spectrum for doubly-robust and weighted version of these estimators. We provide empirical evidence that estimators in this spectrum can be used to trade-off between the bias and variance of IS and SIS and can achieve lower mean-squared error than both IS and SIS.

Distributional Depth-Based Estimation of Object Articulation Models

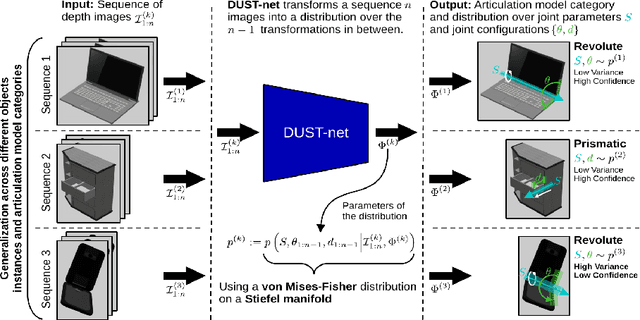
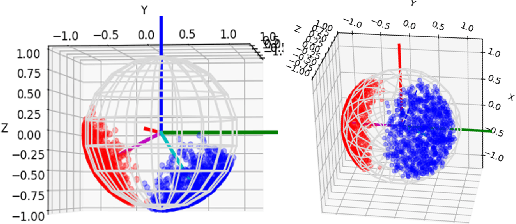
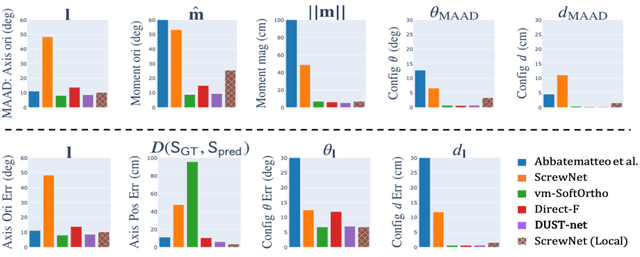
We propose a method that efficiently learns distributions over articulation model parameters directly from depth images without the need to know articulation model categories a priori. By contrast, existing methods that learn articulation models from raw observations typically only predict point estimates of the model parameters, which are insufficient to guarantee the safe manipulation of articulated objects. Our core contributions include a novel representation for distributions over rigid body transformations and articulation model parameters based on screw theory, von Mises-Fisher distributions, and Stiefel manifolds. Combining these concepts allows for an efficient, mathematically sound representation that implicitly satisfies the constraints that rigid body transformations and articulations must adhere to. Leveraging this representation, we introduce a novel deep learning based approach, DUST-net, that performs category-independent articulation model estimation while also providing model uncertainties. We evaluate our approach on several benchmarking datasets and real-world objects and compare its performance with two current state-of-the-art methods. Our results demonstrate that DUST-net can successfully learn distributions over articulation models for novel objects across articulation model categories, which generate point estimates with better accuracy than state-of-the-art methods and effectively capture the uncertainty over predicted model parameters due to noisy inputs.

A Manifold Approach to Learning Mutually Orthogonal Subspaces

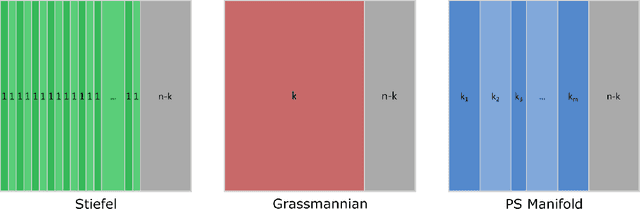
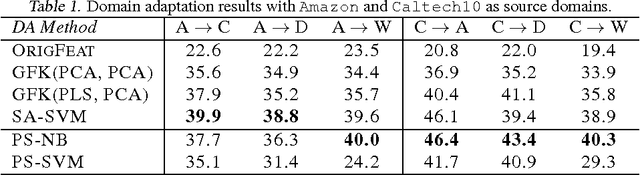
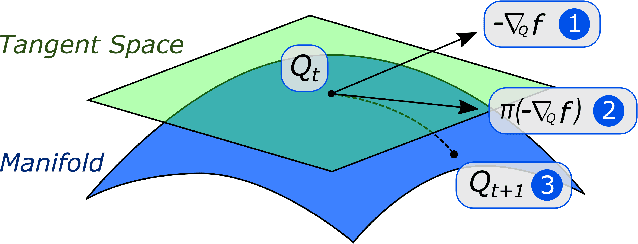
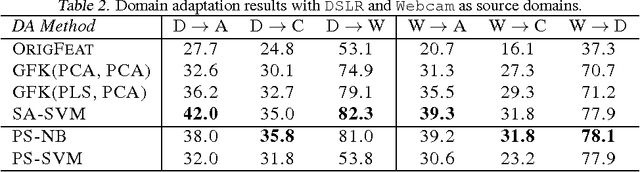
Although many machine learning algorithms involve learning subspaces with particular characteristics, optimizing a parameter matrix that is constrained to represent a subspace can be challenging. One solution is to use Riemannian optimization methods that enforce such constraints implicitly, leveraging the fact that the feasible parameter values form a manifold. While Riemannian methods exist for some specific problems, such as learning a single subspace, there are more general subspace constraints that offer additional flexibility when setting up an optimization problem, but have not been formulated as a manifold. We propose the partitioned subspace (PS) manifold for optimizing matrices that are constrained to represent one or more subspaces. Each point on the manifold defines a partitioning of the input space into mutually orthogonal subspaces, where the number of partitions and their sizes are defined by the user. As a result, distinct groups of features can be learned by defining different objective functions for each partition. We illustrate the properties of the manifold through experiments on multiple dataset analysis and domain adaptation.