A Manifold Approach to Learning Mutually Orthogonal Subspaces
Paper and Code
Mar 08, 2017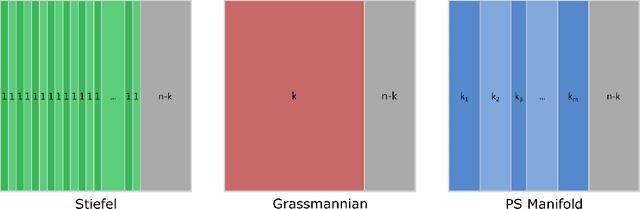
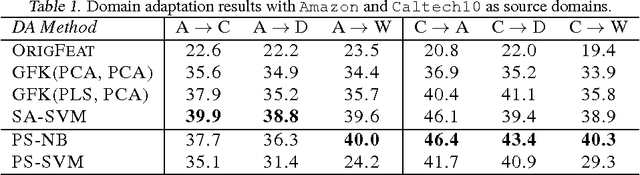
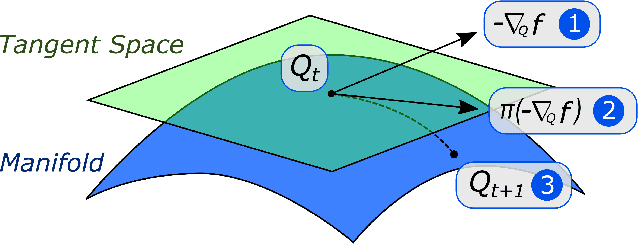
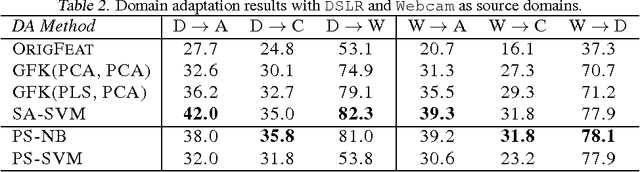
Although many machine learning algorithms involve learning subspaces with particular characteristics, optimizing a parameter matrix that is constrained to represent a subspace can be challenging. One solution is to use Riemannian optimization methods that enforce such constraints implicitly, leveraging the fact that the feasible parameter values form a manifold. While Riemannian methods exist for some specific problems, such as learning a single subspace, there are more general subspace constraints that offer additional flexibility when setting up an optimization problem, but have not been formulated as a manifold. We propose the partitioned subspace (PS) manifold for optimizing matrices that are constrained to represent one or more subspaces. Each point on the manifold defines a partitioning of the input space into mutually orthogonal subspaces, where the number of partitions and their sizes are defined by the user. As a result, distinct groups of features can be learned by defining different objective functions for each partition. We illustrate the properties of the manifold through experiments on multiple dataset analysis and domain adaptation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge