Industry Scale Semi-Supervised Learning for Natural Language Understanding

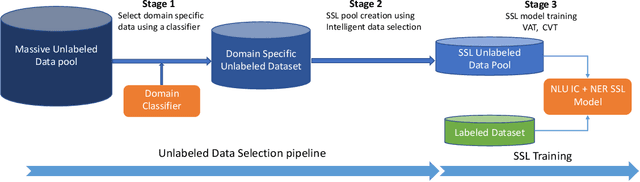
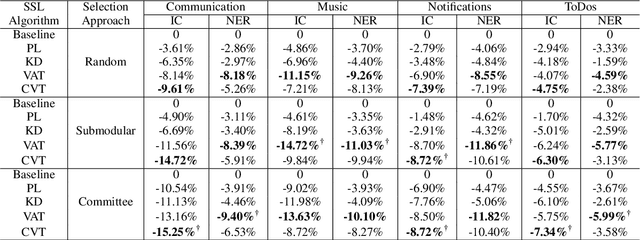
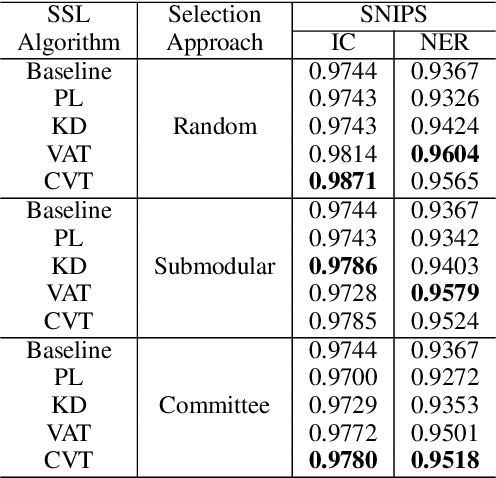
This paper presents a production Semi-Supervised Learning (SSL) pipeline based on the student-teacher framework, which leverages millions of unlabeled examples to improve Natural Language Understanding (NLU) tasks. We investigate two questions related to the use of unlabeled data in production SSL context: 1) how to select samples from a huge unlabeled data pool that are beneficial for SSL training, and 2) how do the selected data affect the performance of different state-of-the-art SSL techniques. We compare four widely used SSL techniques, Pseudo-Label (PL), Knowledge Distillation (KD), Virtual Adversarial Training (VAT) and Cross-View Training (CVT) in conjunction with two data selection methods including committee-based selection and submodular optimization based selection. We further examine the benefits and drawbacks of these techniques when applied to intent classification (IC) and named entity recognition (NER) tasks, and provide guidelines specifying when each of these methods might be beneficial to improve large scale NLU systems.

A Manifold Approach to Learning Mutually Orthogonal Subspaces

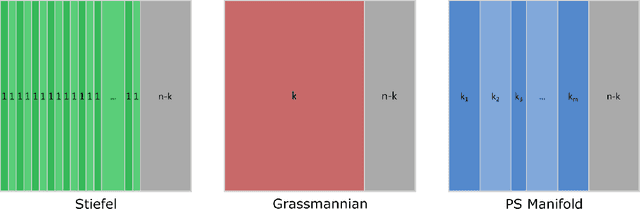
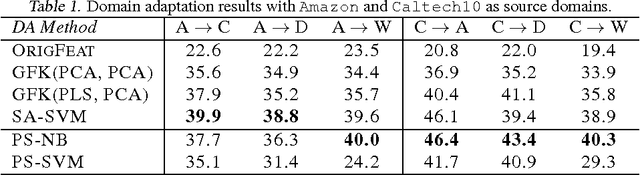
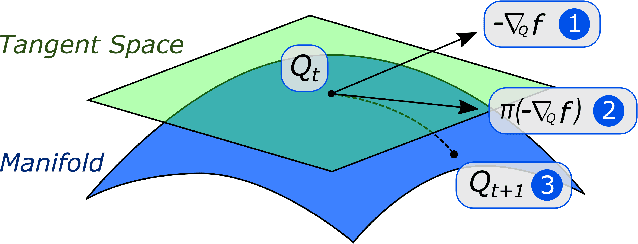
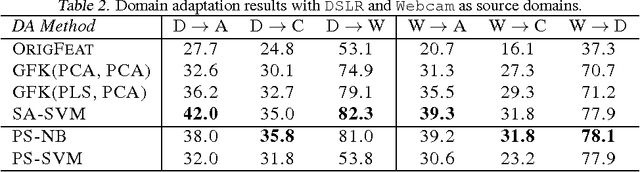
Although many machine learning algorithms involve learning subspaces with particular characteristics, optimizing a parameter matrix that is constrained to represent a subspace can be challenging. One solution is to use Riemannian optimization methods that enforce such constraints implicitly, leveraging the fact that the feasible parameter values form a manifold. While Riemannian methods exist for some specific problems, such as learning a single subspace, there are more general subspace constraints that offer additional flexibility when setting up an optimization problem, but have not been formulated as a manifold. We propose the partitioned subspace (PS) manifold for optimizing matrices that are constrained to represent one or more subspaces. Each point on the manifold defines a partitioning of the input space into mutually orthogonal subspaces, where the number of partitions and their sizes are defined by the user. As a result, distinct groups of features can be learned by defining different objective functions for each partition. We illustrate the properties of the manifold through experiments on multiple dataset analysis and domain adaptation.