One For All: LLM-based Heterogeneous Mission Planning in Precision Agriculture

Artificial intelligence is transforming precision agriculture, offering farmers new tools to streamline their daily operations. While these technological advances promise increased efficiency, they often introduce additional complexity and steep learning curves that are particularly challenging for non-technical users who must balance tech adoption with existing workloads. In this paper, we present a natural language (NL) robotic mission planner that enables non-specialists to control heterogeneous robots through a common interface. By leveraging large language models (LLMs) and predefined primitives, our architecture seamlessly translates human language into intermediate descriptions that can be executed by different robotic platforms. With this system, users can formulate complex agricultural missions without writing any code. In the work presented in this paper, we extend our previous system tailored for wheeled robot mission planning through a new class of experiments involving robotic manipulation and computer vision tasks. Our results demonstrate that the architecture is both general enough to support a diverse set of robots and powerful enough to execute complex mission requests. This work represents a significant step toward making robotic automation in precision agriculture more accessible to non-technical users.

Leveraging LLMs for Mission Planning in Precision Agriculture

Robotics and artificial intelligence hold significant potential for advancing precision agriculture. While robotic systems have been successfully deployed for various tasks, adapting them to perform diverse missions remains challenging, particularly because end users often lack technical expertise. In this paper, we present an end-to-end system that leverages large language models (LLMs), specifically ChatGPT, to enable users to assign complex data collection tasks to autonomous robots using natural language instructions. To enhance reusability, mission plans are encoded using an existing IEEE task specification standard, and are executed on robots via ROS2 nodes that bridge high-level mission descriptions with existing ROS libraries. Through extensive experiments, we highlight the strengths and limitations of LLMs in this context, particularly regarding spatial reasoning and solving complex routing challenges, and show how our proposed implementation overcomes them.

Solving Stochastic Orienteering Problems with Chance Constraints Using Monte Carlo Tree Search

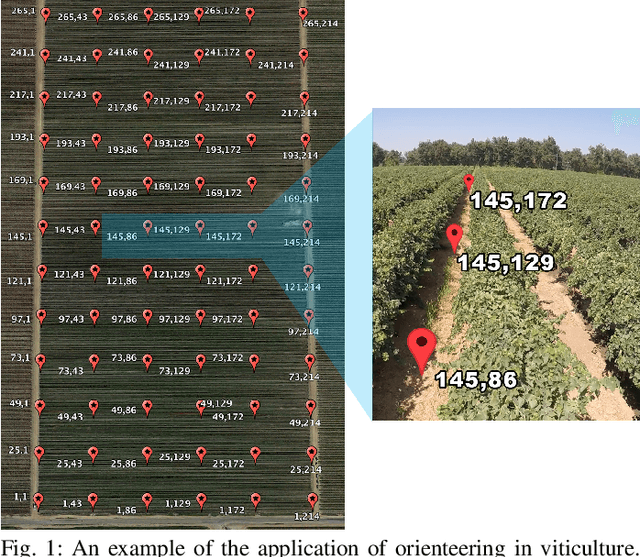
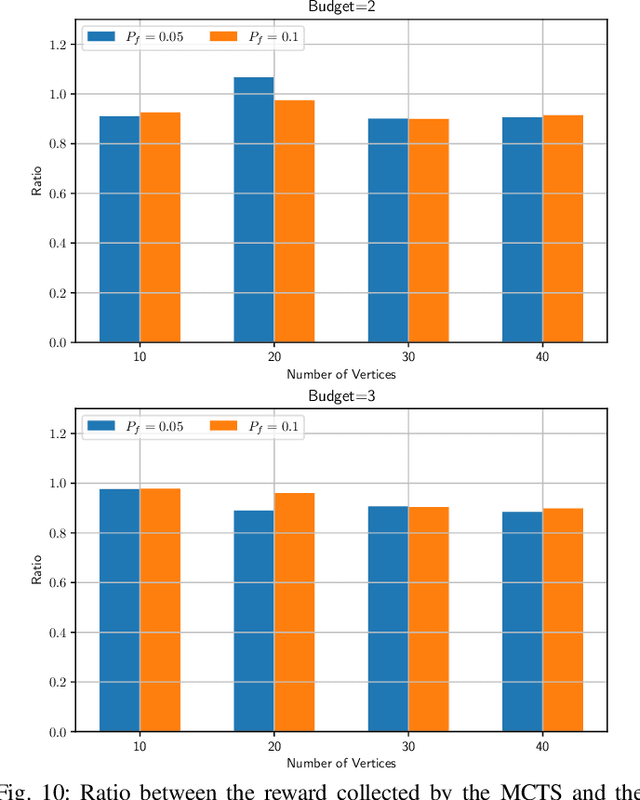
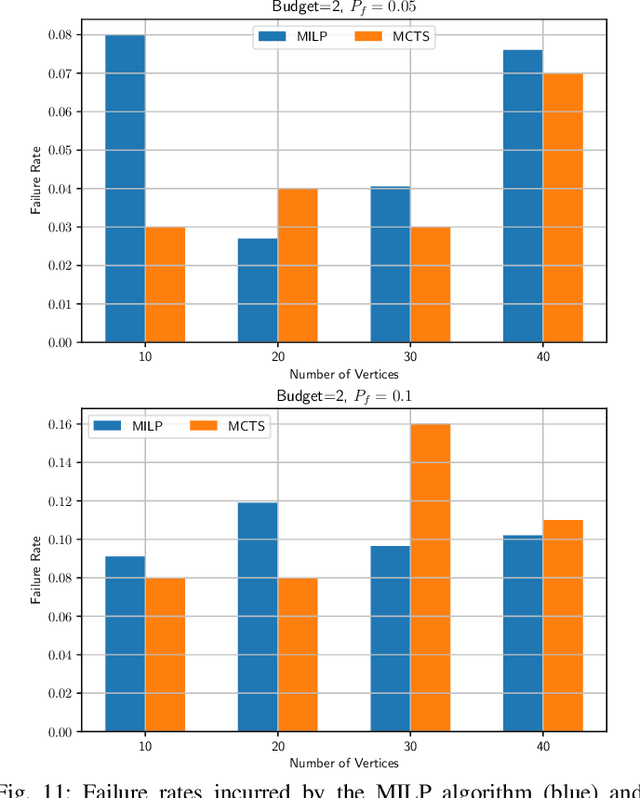
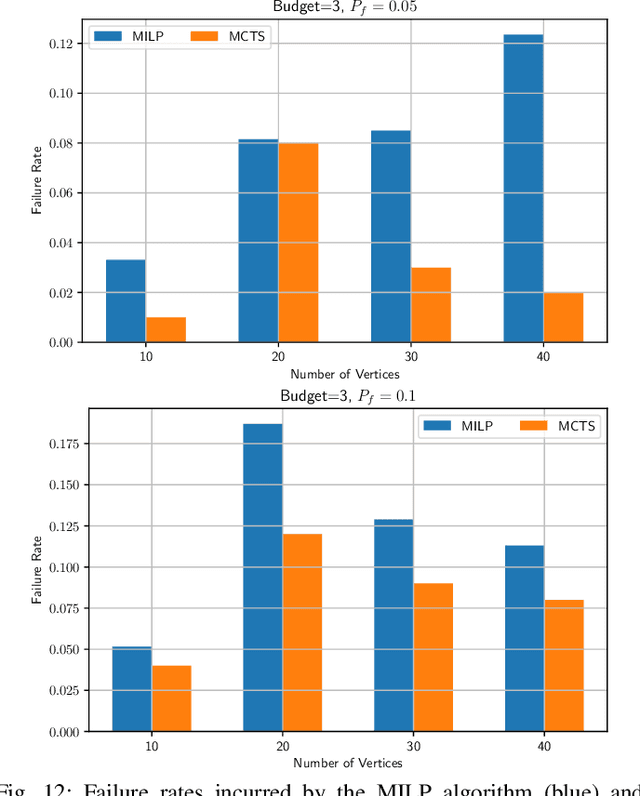
We present a new Monte Carlo Tree Search (MCTS) algorithm to solve the stochastic orienteering problem with chance constraints, i.e., a version of the problem where travel costs are random, and one is assigned a bound on the tolerable probability of exceeding the budget. The algorithm we present is online and anytime, i.e., it alternates planning and execution, and the quality of the solution it produces increases as the allowed computational time increases. Differently from most former MCTS algorithms, for each action available in a state the algorithm maintains estimates of both its value and the probability that its execution will eventually result in a violation of the chance constraint. Then, at action selection time, our proposed solution prunes away trajectories that are estimated to violate the failure probability. Extensive simulation results show that this approach can quickly produce high-quality solutions and is competitive with the optimal but time-consuming solution.

Distributed Multi-robot Online Sampling with Budget Constraints

In multi-robot informative path planning the problem is to find a route for each robot in a team to visit a set of locations that can provide the most useful data to reconstruct an unknown scalar field. In the budgeted version, each robot is subject to a travel budget limiting the distance it can travel. Our interest in this problem is motivated by applications in precision agriculture, where robots are used to collect measurements to estimate domain-relevant scalar parameters such as soil moisture or nitrates concentrations. In this paper, we propose an online, distributed multi-robot sampling algorithm based on Monte Carlo Tree Search (MCTS) where each robot iteratively selects the next sampling location through communication with other robots and considering its remaining budget. We evaluate our proposed method for varying team sizes and in different environments, and we compare our solution with four different baseline methods. Our experiments show that our solution outperforms the baselines when the budget is tight by collecting measurements leading to smaller reconstruction errors.

Improving the ROS 2 Navigation Stack with Real-Time Local Costmap Updates for Agricultural Applications

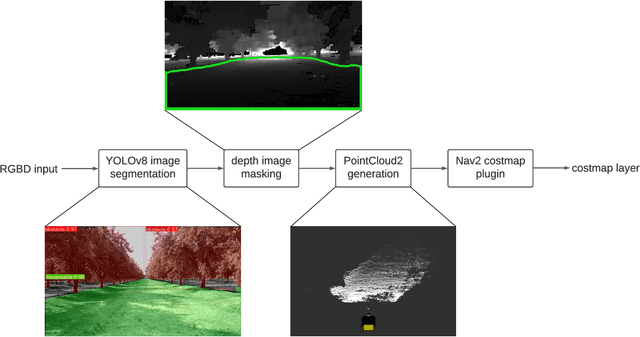
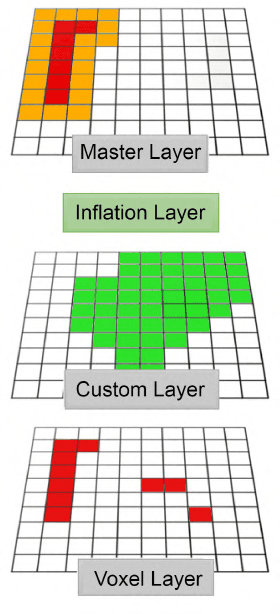
The ROS 2 Navigation Stack (Nav2) has emerged as a widely used software component providing the underlying basis to develop a variety of high-level functionalities. However, when used in outdoor environments such as orchards and vineyards, its functionality is notably limited by the presence of obstacles and/or situations not commonly found in indoor settings. One such example is given by tall grass and weeds that can be safely traversed by a robot, but that can be perceived as obstacles by LiDAR sensors, and then force the robot to take longer paths to avoid them, or abort navigation altogether. To overcome these limitations, domain specific extensions must be developed and integrated into the software pipeline. This paper presents a new, lightweight approach to address this challenge and improve outdoor robot navigation. Leveraging the multi-scale nature of the costmaps supporting Nav2, we developed a system that using a depth camera performs pixel level classification on the images, and in real time injects corrections into the local cost map, thus enabling the robot to traverse areas that would otherwise be avoided by the Nav2. Our approach has been implemented and validated on a Clearpath Husky and we demonstrate that with this extension the robot is able to perform navigation tasks that would be otherwise not practical with the standard components.

Informative path planning for scalar dynamic reconstruction using coregionalized Gaussian processes and a spatiotemporal kernel

The proliferation of unmanned vehicles offers many opportunities for solving environmental sampling tasks with applications in resource monitoring and precision agriculture. Informative path planning (IPP) includes a family of methods which offer improvements over traditional surveying techniques for suggesting locations for observation collection. In this work, we present a novel solution to the IPP problem by using a coregionalized Gaussian processes to estimate a dynamic scalar field that varies in space and time. Our method improves previous approaches by using a composite kernel accounting for spatiotemporal correlations and at the same time, can be readily incorporated in existing IPP algorithms. Through extensive simulations, we show that our novel modeling approach leads to more accurate estimations when compared with formerly proposed methods that do not account for the temporal dimension.

Speeding up Routing Schedules on Aisle-Graphs with Single Access

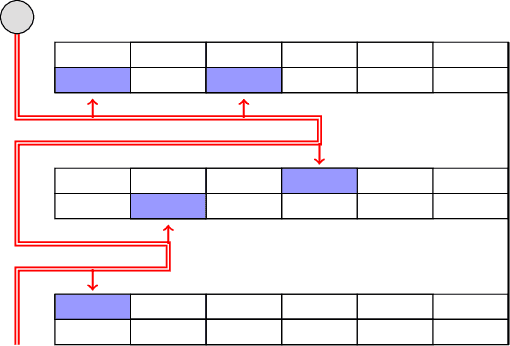
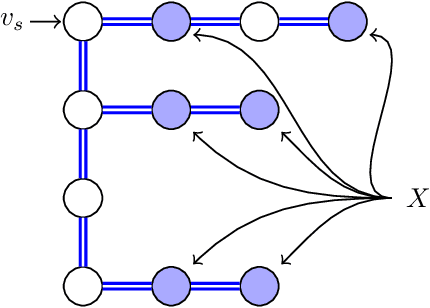
In this paper, we study the Orienteering Aisle-graphs Single-access Problem (OASP), a variant of the orienteering problem for a robot moving in a so-called single-access aisle-graph, i.e., a graph consisting of a set of rows that can be accessed from one side only. Aisle-graphs model, among others, vineyards or warehouses. Each aisle-graph vertex is associated with a reward that a robot obtains when visits the vertex itself. As the robot's energy is limited, only a subset of vertices can be visited with a fully charged battery. The objective is to maximize the total reward collected by the robot with a battery charge. We first propose an optimal algorithm that solves OASP in O(m^2 n^2) time for aisle-graphs with a single access consisting of m rows, each with n vertices. With the goal of designing faster solutions, we propose four greedy sub-optimal algorithms that run in at most O(mn (m+n)) time. For two of them, we guarantee an approximation ratio of 1/2(1-1/e), where e is the base of the natural logarithm, on the total reward by exploiting the well-known submodularity property. Experimentally, we show that these algorithms collect more than 80% of the optimal reward.

Task Planning on Stochastic Aisle Graphs for Precision Agriculture

This work addresses task planning under uncertainty for precision agriculture applications whereby task costs are uncertain and the gain of completing a task is proportional to resource consumption (such as water consumption in precision irrigation). The goal is to complete all tasks while prioritizing those that are more urgent, and subject to diverse budget thresholds and stochastic costs for tasks. To describe agriculture-related environments that incorporate stochastic costs to complete tasks, a new Stochastic-Vertex-Cost Aisle Graph (SAG) is introduced. Then, a task allocation algorithm, termed Next-Best-Action Planning (NBA-P), is proposed. NBA-P utilizes the underlying structure enabled by SAG, and tackles the task planning problem by simultaneously determining the optimal tasks to perform and an optimal time to exit (i.e. return to a base station), at run-time. The proposed approach is tested with both simulated data and real-world experimental datasets collected in a commercial vineyard, in both single- and multi-robot scenarios. In all cases, NBA-P outperforms other evaluated methods in terms of return per visited vertex, wasted resources resulting from aborted tasks (i.e. when a budget threshold is exceeded), and total visited vertices.

Optimal Routing Schedules for Robots Operating in Aisle-Structures

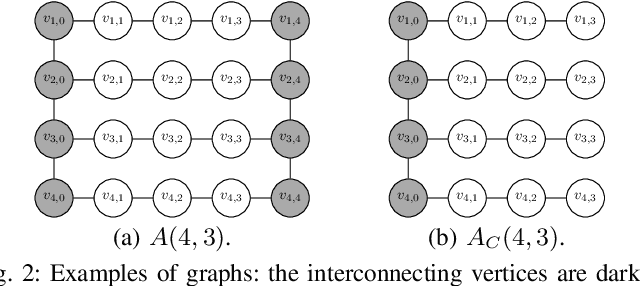
In this paper, we consider the Constant-cost Orienteering Problem (COP) where a robot, constrained by a limited travel budget, aims at selecting a path with the largest reward in an aisle-graph. The aisle-graph consists of a set of loosely connected rows where the robot can change lane only at either end, but not in the middle. Even when considering this special type of graphs, the orienteering problem is known to be NP-hard. We optimally solve in polynomial time two special cases, COP-FR where the robot can only traverse full rows, and COP-SC where the robot can access the rows only from one side. To solve the general COP, we then apply our special case algorithms as well as a new heuristic that suitably combines them. Despite its light computational complexity and being confined into a very limited class of paths, the optimal solutions for COP-FR turn out to be competitive even for COP in both real and synthetic scenarios. Furthermore, our new heuristic for the general case outperforms state-of-art algorithms, especially for input with highly unbalanced rewards.

Multi-Fingered Robotic Grasping: A Primer

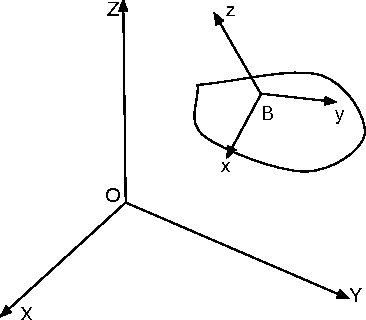
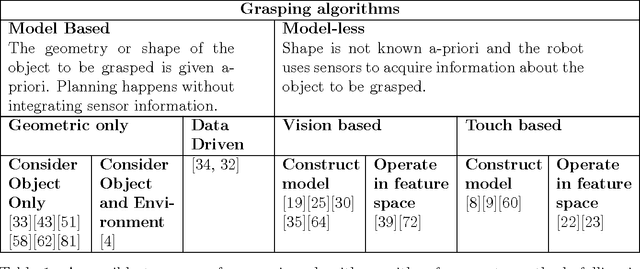
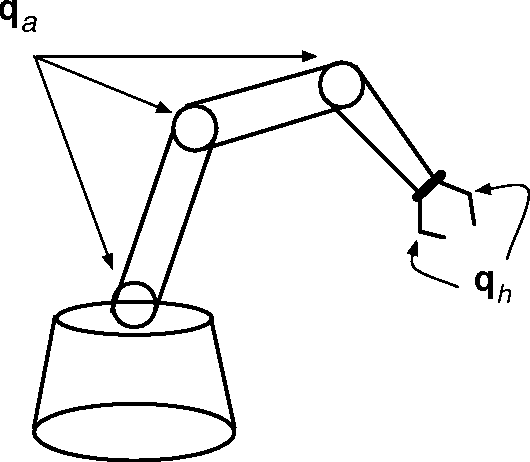
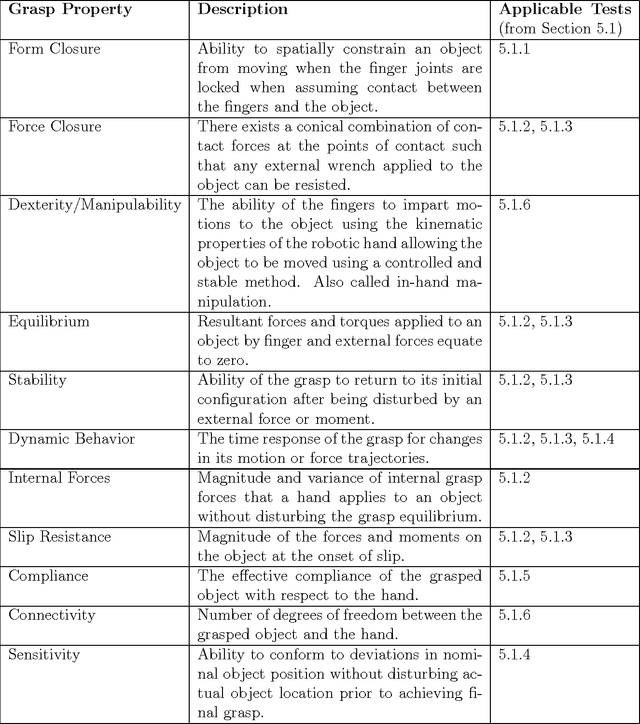
This technical report presents an introduction to different aspects of multi-fingered robot grasping. After having introduced relevant mathematical background for modeling, form and force closure are discussed. Next, we present an overview of various grasp planning algorithms with the objective of illustrating different approaches to solve this problem. Finally, we discuss grasp performance benchmarking.