A Novel Multi-Layer Framework for BVLoS Drone Operation: A Preliminary Study

Drones have become increasingly popular in a variety of fields, including agriculture, emergency response, and package delivery. However, most drone operations are currently limited to within Visual Line of Sight (vlos) due to safety concerns. Flying drones Beyond Visual Line of Sight (bvlos) presents new challenges and opportunities, but also requires new technologies and regulatory frameworks, not yet implemented, to ensure that the drone is constantly under the control of a remote operator. In this preliminary study, we assume to remotely control the drone using the available ground cellular network infrastructure. We propose to plan bvlos drone operations using a novel multi-layer framework that includes many layers of constraints that closely resemble real-world scenarios and challenges. These layers include information such as the potential ground risk in the event of a drone failure, the available ground cellular network infrastructure, and the presence of ground obstacles. From the multi-layer framework, a graph is constructed whose edges are weighted with a dependability score that takes into account the information of the multi-layer framework. Then, the planning of bvlos drone missions is equivalent to solving the Maximum Path Dependability Problem on the constructed graph, which turns out to be solvable by applying Dijkstra's algorithm.

A Comprehensive Investigation on Range-free Localization Algorithms with Mobile Anchors at Different Altitudes

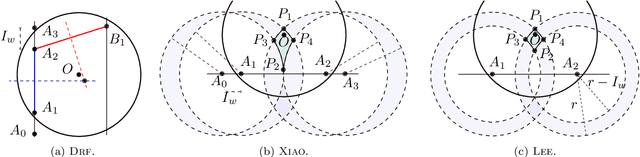
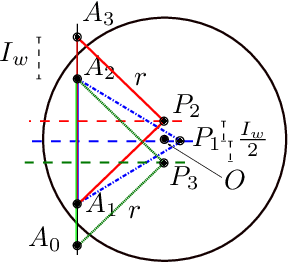
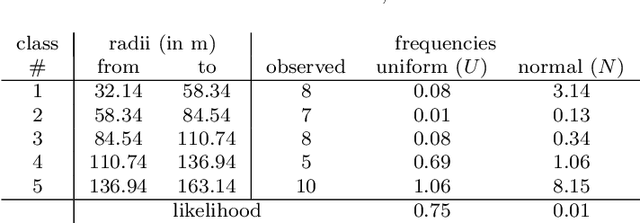
In this work, the problem of localizing ground devices (GDs) is studied comparing the performance of four range-free (RF) localization algorithms that use a mobile anchor (MA). All the investigated algorithms are based on the so-called heard/not-heard (HnH) method, which allows the GDs to detect the MA at the border of their antenna communication radius. Despite the simplicity of this method, its efficacy in terms of accuracy is poor because it relies on the antenna radius that continuously varies under different conditions. Usually, the antenna radius declared by the manufacturer does not fully characterize the actual antenna radiation pattern. In this paper, the radiation pattern of the commercial DecaWave DWM1001 Ultra-Wide-Band (UWB) antennas is observed in a real test-bed at different altitudes for collecting more information and insights on the antenna radius. The compared algorithms are then tested using both the observed and the manufacturer radii. The experimental accuracy is close to the expected theoretical one only when the antenna pattern is actually omnidirectional. However, typical antennas have strong pattern irregularities that decrease the accuracy. For improving the performance, we propose range-based (RB) variants of the compared algorithms in which, instead of using the observed or the manufacturer radii, the actual measured distances between the MA and the GD are used. The localization accuracy tremendously improves confirming that the knowledge of the exact antenna pattern is essential for any RF algorithm.

Speeding up Routing Schedules on Aisle-Graphs with Single Access

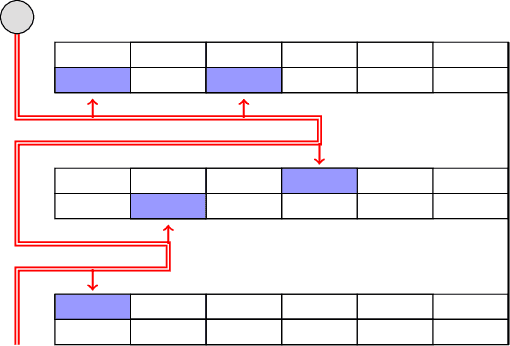
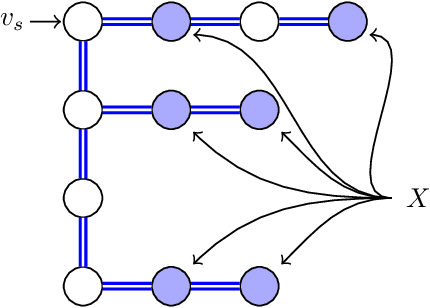
In this paper, we study the Orienteering Aisle-graphs Single-access Problem (OASP), a variant of the orienteering problem for a robot moving in a so-called single-access aisle-graph, i.e., a graph consisting of a set of rows that can be accessed from one side only. Aisle-graphs model, among others, vineyards or warehouses. Each aisle-graph vertex is associated with a reward that a robot obtains when visits the vertex itself. As the robot's energy is limited, only a subset of vertices can be visited with a fully charged battery. The objective is to maximize the total reward collected by the robot with a battery charge. We first propose an optimal algorithm that solves OASP in O(m^2 n^2) time for aisle-graphs with a single access consisting of m rows, each with n vertices. With the goal of designing faster solutions, we propose four greedy sub-optimal algorithms that run in at most O(mn (m+n)) time. For two of them, we guarantee an approximation ratio of 1/2(1-1/e), where e is the base of the natural logarithm, on the total reward by exploiting the well-known submodularity property. Experimentally, we show that these algorithms collect more than 80% of the optimal reward.

Heuristic Algorithms for Co-scheduling of Edge Analytics and Routes for UAV Fleet Missions

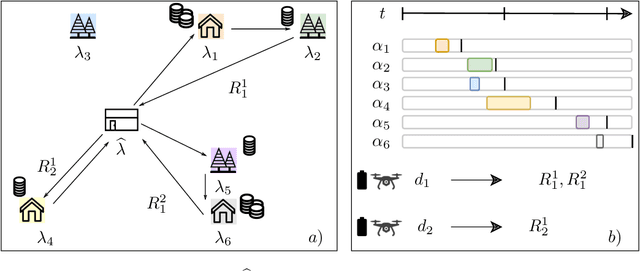
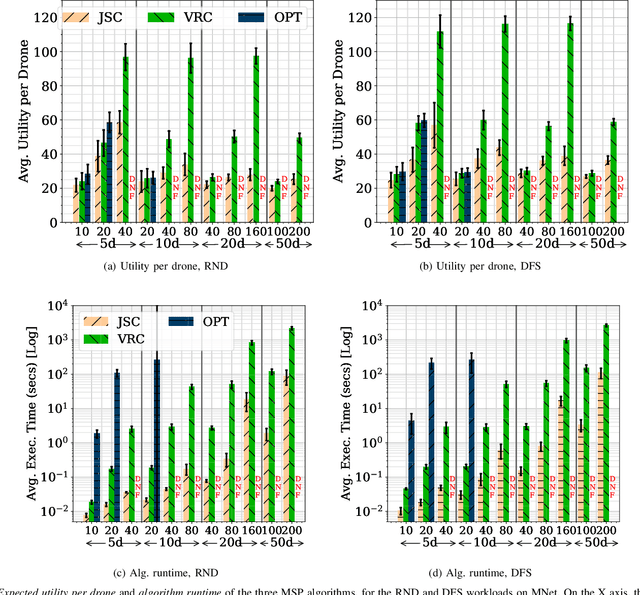
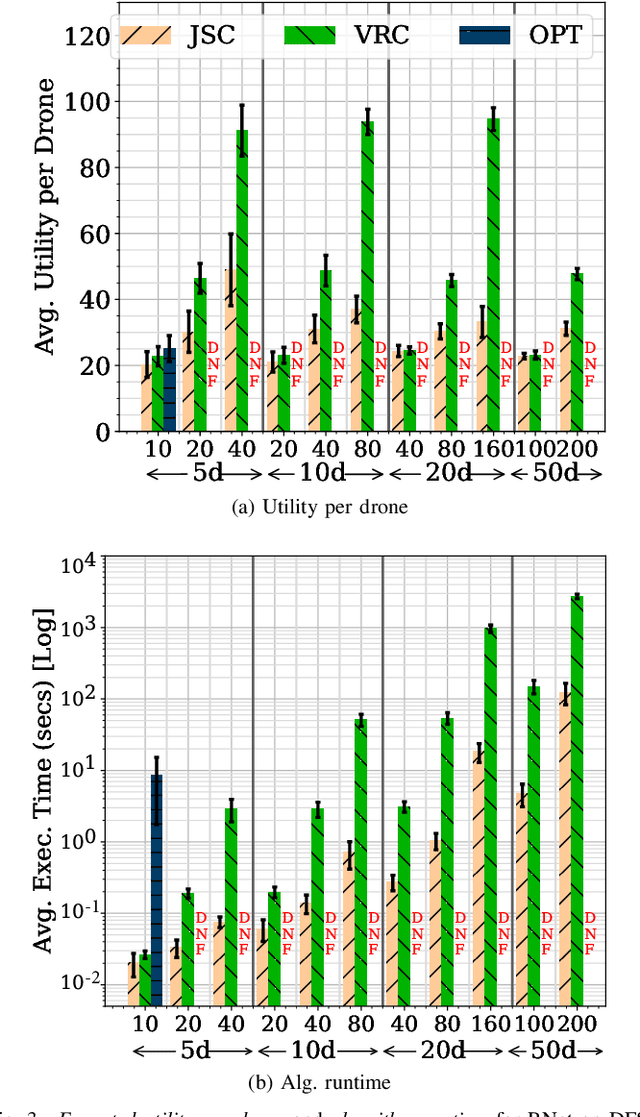
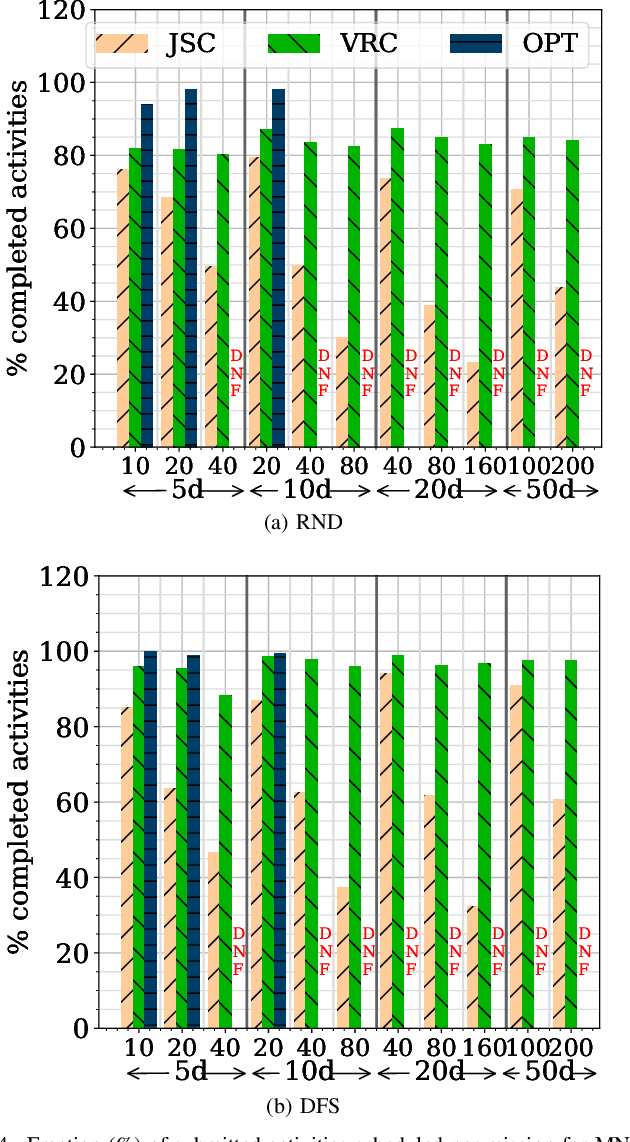
Unmanned Aerial Vehicles (UAVs) or drones are increasingly used for urban applications like traffic monitoring and construction surveys. Autonomous navigation allows drones to visit waypoints and accomplish activities as part of their mission. A common activity is to hover and observe a location using on-board cameras. Advances in Deep Neural Networks (DNNs) allow such videos to be analyzed for automated decision making. UAVs also host edge computing capability for on-board inferencing by such DNNs. To this end, for a fleet of drones, we propose a novel Mission Scheduling Problem (MSP) that co-schedules the flight routes to visit and record video at waypoints, and their subsequent on-board edge analytics. The proposed schedule maximizes the utility from the activities while meeting activity deadlines as well as energy and computing constraints. We first prove that MSP is NP-hard and then optimally solve it by formulating a mixed integer linear programming (MILP) problem. Next, we design two efficient heuristic algorithms, JSC and VRC, that provide fast sub-optimal solutions. Evaluation of these three schedulers using real drone traces demonstrate utility-runtime trade-offs under diverse workloads.

Energy-Constrained Delivery of Goods with Drones Under Varying Wind Conditions

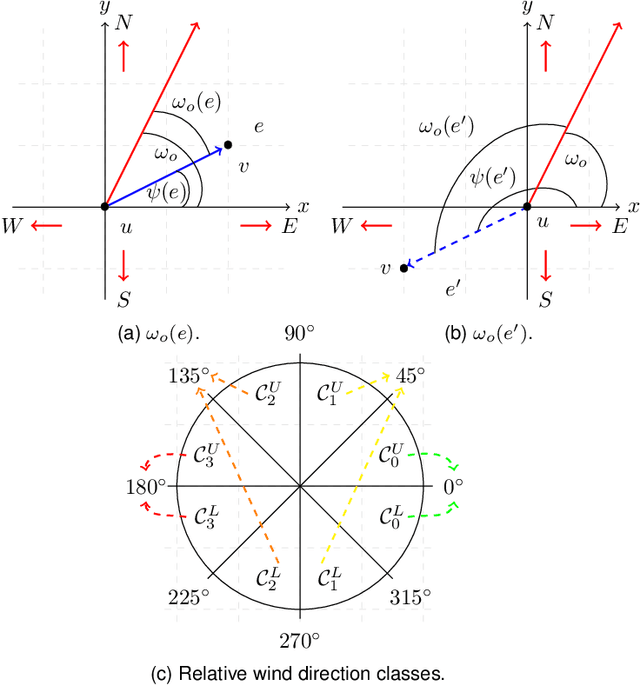
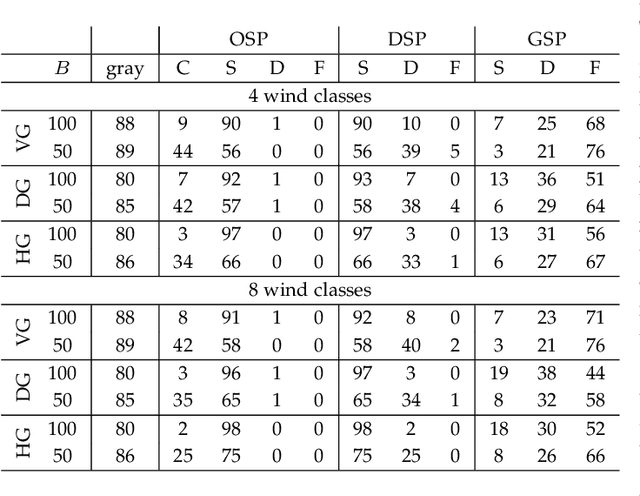
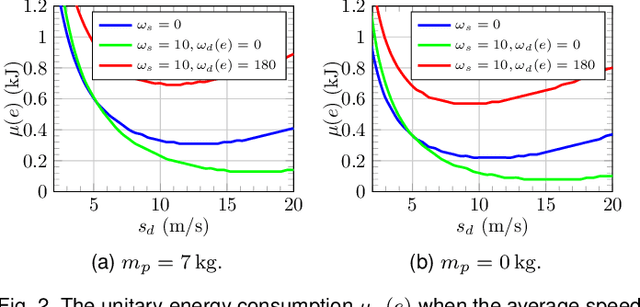
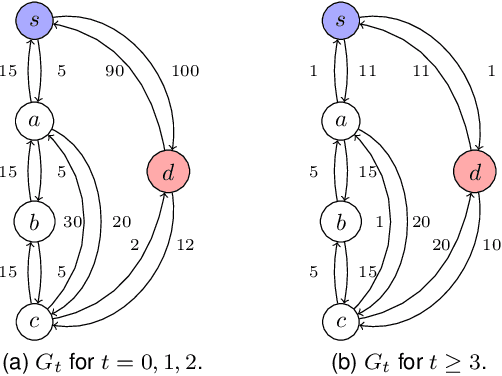
In this paper, we study the feasibility of sending drones to deliver goods from a depot to a customer by solving what we call the Mission-Feasibility Problem (MFP). Due to payload constraints, the drone can serve only one customer at a time. To this end, we propose a novel framework based on time-dependent cost graphs to properly model the MFP and tackle the delivery dynamics. When the drone moves in the delivery area, the global wind may change thereby affecting the drone's energy consumption, which in turn can increase or decrease. This issue is addressed by designing three algorithms, namely: (i) compute the route of minimum energy once, at the beginning of the mission, (ii) dynamically reconsider the most convenient trip towards the destination, and (iii) dynamically select only the best local choice. We evaluate the performance of our algorithms on both synthetic and real-world data. The changes in the drone's energy consumption are reflected by changes in the cost of the edges of the graphs. The algorithms receive the new costs every time the drone flies over a new vertex, and they have no full knowledge in advance of the weights. We compare them in terms of the percentage of missions that are completed with success (the drone delivers the goods and comes back to the depot), with delivered (the drone delivers the goods but cannot come back to the depot), and with failure (the drone neither delivers the goods nor comes back to the depot).

Optimal Routing Schedules for Robots Operating in Aisle-Structures

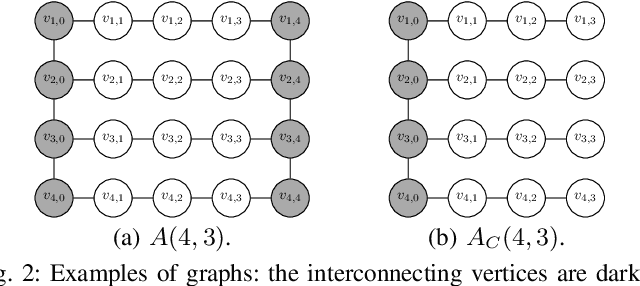
In this paper, we consider the Constant-cost Orienteering Problem (COP) where a robot, constrained by a limited travel budget, aims at selecting a path with the largest reward in an aisle-graph. The aisle-graph consists of a set of loosely connected rows where the robot can change lane only at either end, but not in the middle. Even when considering this special type of graphs, the orienteering problem is known to be NP-hard. We optimally solve in polynomial time two special cases, COP-FR where the robot can only traverse full rows, and COP-SC where the robot can access the rows only from one side. To solve the general COP, we then apply our special case algorithms as well as a new heuristic that suitably combines them. Despite its light computational complexity and being confined into a very limited class of paths, the optimal solutions for COP-FR turn out to be competitive even for COP in both real and synthetic scenarios. Furthermore, our new heuristic for the general case outperforms state-of-art algorithms, especially for input with highly unbalanced rewards.