Rate, Explain and Cite (REC): Enhanced Explanation and Attribution in Automatic Evaluation by Large Language Models

LLMs have demonstrated impressive proficiency in generating coherent and high-quality text, making them valuable across a range of text-generation tasks. However, rigorous evaluation of this generated content is crucial, as ensuring its quality remains a significant challenge due to persistent issues such as factual inaccuracies and hallucinations. This paper introduces two fine-tuned general-purpose LLM autoevaluators, REC-12B and REC-70B, specifically designed to evaluate generated text across several dimensions: faithfulness, instruction following, coherence, and completeness. These models not only provide ratings for these metrics but also offer detailed explanations and verifiable citations, thereby enhancing trust in the content. Moreover, the models support various citation modes, accommodating different requirements for latency and granularity. Extensive evaluations on diverse benchmarks demonstrate that our general-purpose LLM auto-evaluator, REC-70B, outperforms state-of-the-art LLMs, excelling in content evaluation by delivering better quality explanations and citations with minimal bias. It achieves Rank \#1 as a generative model on the RewardBench leaderboard\footnote{\url{https://huggingface.co/spaces/allenai/reward-bench}} under the model name \texttt{TextEval-Llama3.1-70B}. Our REC dataset and models are released at \url{https://github.com/adelaidehsu/REC}.

A Comprehensive Survey of LLM Alignment Techniques: RLHF, RLAIF, PPO, DPO and More

With advancements in self-supervised learning, the availability of trillions tokens in a pre-training corpus, instruction fine-tuning, and the development of large Transformers with billions of parameters, large language models (LLMs) are now capable of generating factual and coherent responses to human queries. However, the mixed quality of training data can lead to the generation of undesired responses, presenting a significant challenge. Over the past two years, various methods have been proposed from different perspectives to enhance LLMs, particularly in aligning them with human expectation. Despite these efforts, there has not been a comprehensive survey paper that categorizes and details these approaches. In this work, we aim to address this gap by categorizing these papers into distinct topics and providing detailed explanations of each alignment method, thereby helping readers gain a thorough understanding of the current state of the field.

On Lipschitz Continuity and Smoothness of Loss Functions in Learning to Rank

In binary classification and regression problems, it is well understood that Lipschitz continuity and smoothness of the loss function play key roles in governing generalization error bounds for empirical risk minimization algorithms. In this paper, we show how these two properties affect generalization error bounds in the learning to rank problem. The learning to rank problem involves vector valued predictions and therefore the choice of the norm with respect to which Lipschitz continuity and smoothness are defined becomes crucial. Choosing the $\ell_\infty$ norm in our definition of Lipschitz continuity allows us to improve existing bounds. Furthermore, under smoothness assumptions, our choice enables us to prove rates that interpolate between $1/\sqrt{n}$ and $1/n$ rates. Application of our results to ListNet, a popular learning to rank method, gives state-of-the-art performance guarantees.

Online Learning to Rank with Top-k Feedback

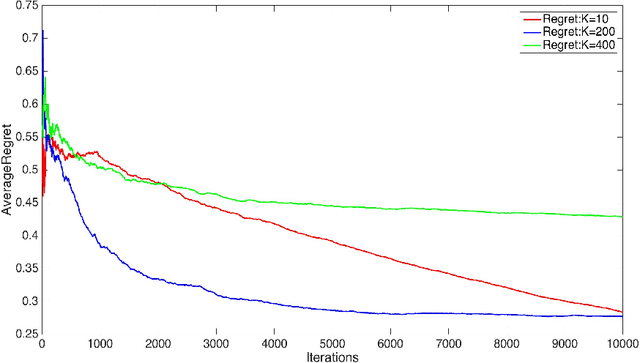
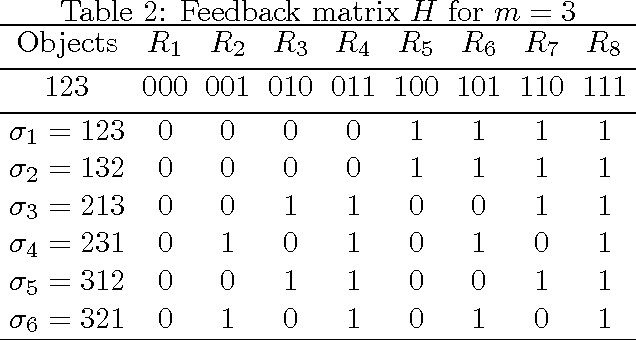
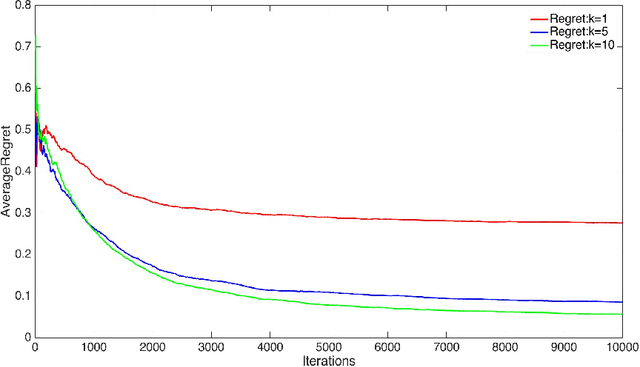
We consider two settings of online learning to rank where feedback is restricted to top ranked items. The problem is cast as an online game between a learner and sequence of users, over $T$ rounds. In both settings, the learners objective is to present ranked list of items to the users. The learner's performance is judged on the entire ranked list and true relevances of the items. However, the learner receives highly restricted feedback at end of each round, in form of relevances of only the top $k$ ranked items, where $k \ll m$. The first setting is \emph{non-contextual}, where the list of items to be ranked is fixed. The second setting is \emph{contextual}, where lists of items vary, in form of traditional query-document lists. No stochastic assumption is made on the generation process of relevances of items and contexts. We provide efficient ranking strategies for both the settings. The strategies achieve $O(T^{2/3})$ regret, where regret is based on popular ranking measures in first setting and ranking surrogates in second setting. We also provide impossibility results for certain ranking measures and a certain class of surrogates, when feedback is restricted to the top ranked item, i.e. $k=1$. We empirically demonstrate the performance of our algorithms on simulated and real world datasets.

Phased Exploration with Greedy Exploitation in Stochastic Combinatorial Partial Monitoring Games

Partial monitoring games are repeated games where the learner receives feedback that might be different from adversary's move or even the reward gained by the learner. Recently, a general model of combinatorial partial monitoring (CPM) games was proposed \cite{lincombinatorial2014}, where the learner's action space can be exponentially large and adversary samples its moves from a bounded, continuous space, according to a fixed distribution. The paper gave a confidence bound based algorithm (GCB) that achieves $O(T^{2/3}\log T)$ distribution independent and $O(\log T)$ distribution dependent regret bounds. The implementation of their algorithm depends on two separate offline oracles and the distribution dependent regret additionally requires existence of a unique optimal action for the learner. Adopting their CPM model, our first contribution is a Phased Exploration with Greedy Exploitation (PEGE) algorithmic framework for the problem. Different algorithms within the framework achieve $O(T^{2/3}\sqrt{\log T})$ distribution independent and $O(\log^2 T)$ distribution dependent regret respectively. Crucially, our framework needs only the simpler "argmax" oracle from GCB and the distribution dependent regret does not require existence of a unique optimal action. Our second contribution is another algorithm, PEGE2, which combines gap estimation with a PEGE algorithm, to achieve an $O(\log T)$ regret bound, matching the GCB guarantee but removing the dependence on size of the learner's action space. However, like GCB, PEGE2 requires access to both offline oracles and the existence of a unique optimal action. Finally, we discuss how our algorithm can be efficiently applied to a CPM problem of practical interest: namely, online ranking with feedback at the top.

Perceptron like Algorithms for Online Learning to Rank

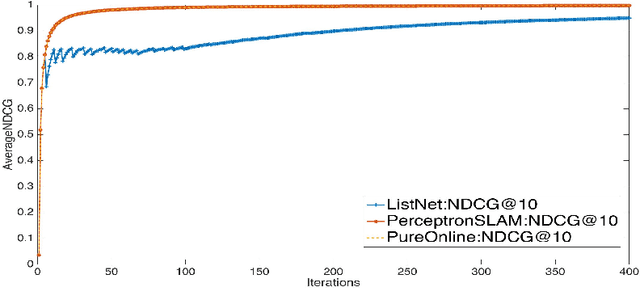
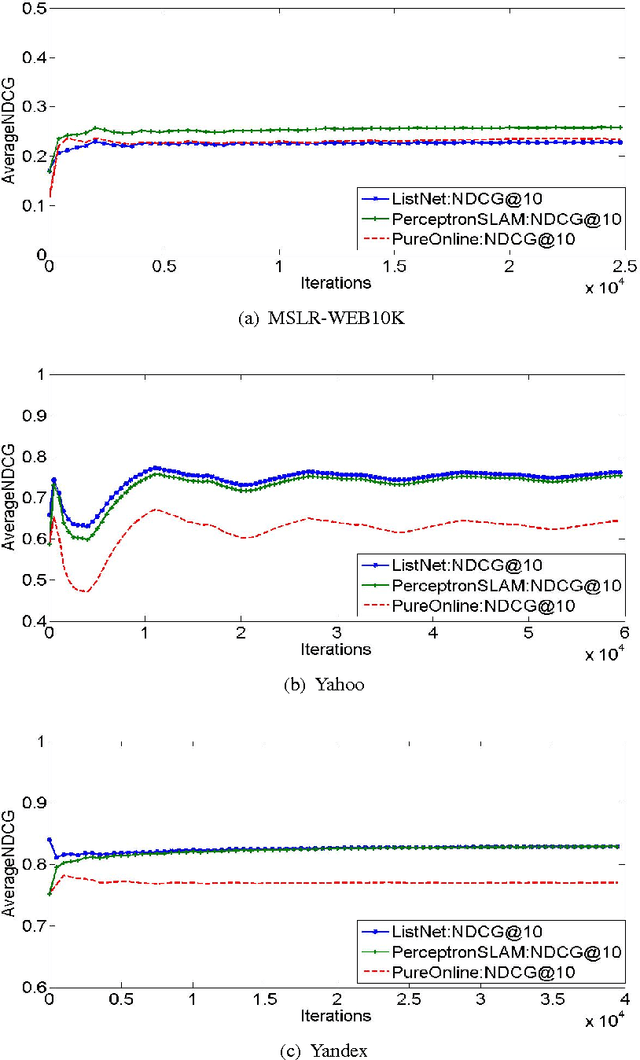
Perceptron is a classic online algorithm for learning a classification function. In this paper, we provide a novel extension of the perceptron algorithm to the learning to rank problem in information retrieval. We consider popular listwise performance measures such as Normalized Discounted Cumulative Gain (NDCG) and Average Precision (AP). A modern perspective on perceptron for classification is that it is simply an instance of online gradient descent (OGD), during mistake rounds, using the hinge loss function. Motivated by this interpretation, we propose a novel family of listwise, large margin ranking surrogates. Members of this family can be thought of as analogs of the hinge loss. Exploiting a certain self-bounding property of the proposed family, we provide a guarantee on the cumulative NDCG (or AP) induced loss incurred by our perceptron-like algorithm. We show that, if there exists a perfect oracle ranker which can correctly rank each instance in an online sequence of ranking data, with some margin, the cumulative loss of perceptron algorithm on that sequence is bounded by a constant, irrespective of the length of the sequence. This result is reminiscent of Novikoff's convergence theorem for the classification perceptron. Moreover, we prove a lower bound on the cumulative loss achievable by any deterministic algorithm, under the assumption of existence of perfect oracle ranker. The lower bound shows that our perceptron bound is not tight, and we propose another, \emph{purely online}, algorithm which achieves the lower bound. We provide empirical results on simulated and large commercial datasets to corroborate our theoretical results.

Online Ranking with Top-1 Feedback

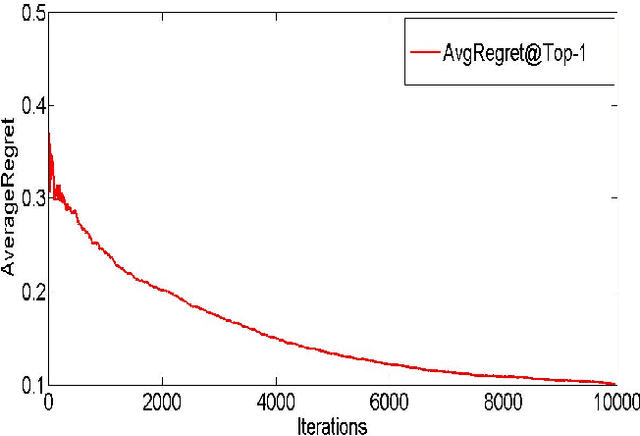
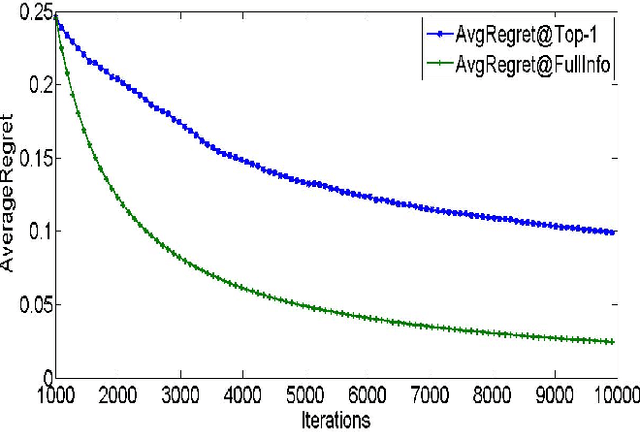
We consider a setting where a system learns to rank a fixed set of $m$ items. The goal is produce good item rankings for users with diverse interests who interact online with the system for $T$ rounds. We consider a novel top-$1$ feedback model: at the end of each round, the relevance score for only the top ranked object is revealed. However, the performance of the system is judged on the entire ranked list. We provide a comprehensive set of results regarding learnability under this challenging setting. For PairwiseLoss and DCG, two popular ranking measures, we prove that the minimax regret is $\Theta(T^{2/3})$. Moreover, the minimax regret is achievable using an efficient strategy that only spends $O(m \log m)$ time per round. The same efficient strategy achieves $O(T^{2/3})$ regret for Precision@$k$. Surprisingly, we show that for normalized versions of these ranking measures, i.e., AUC, NDCG \& MAP, no online ranking algorithm can have sublinear regret.

Personalized Advertisement Recommendation: A Ranking Approach to Address the Ubiquitous Click Sparsity Problem

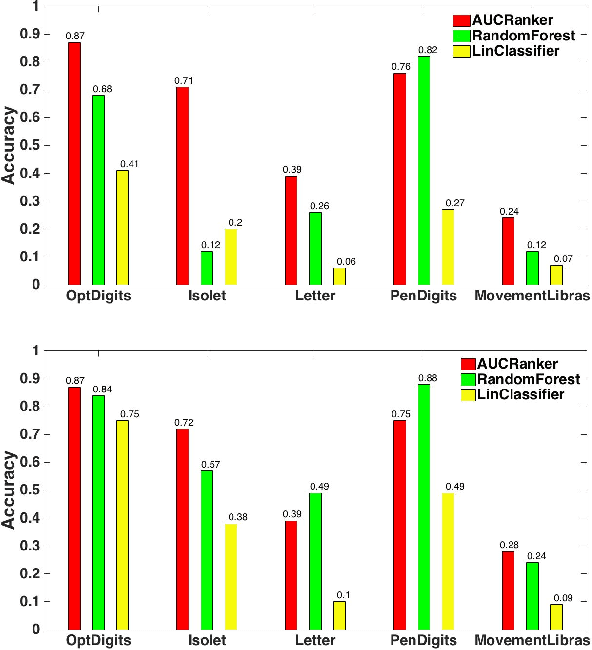
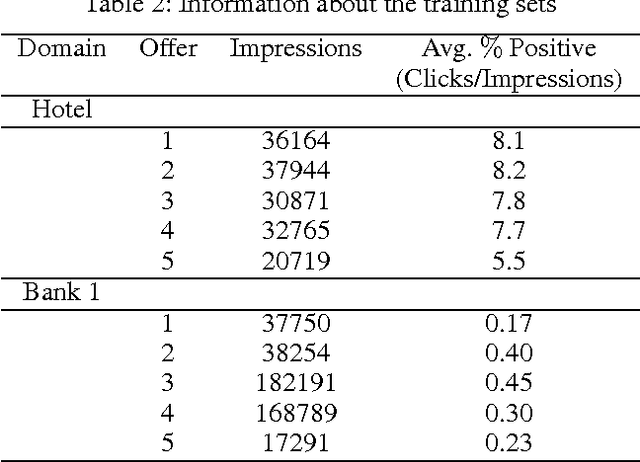
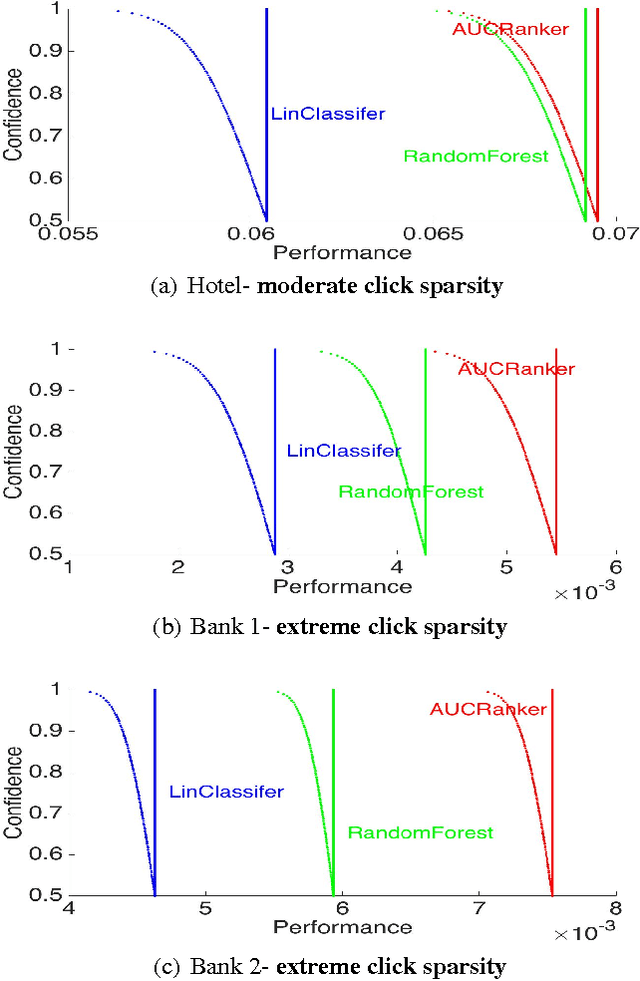
We study the problem of personalized advertisement recommendation (PAR), which consist of a user visiting a system (website) and the system displaying one of $K$ ads to the user. The system uses an internal ad recommendation policy to map the user's profile (context) to one of the ads. The user either clicks or ignores the ad and correspondingly, the system updates its recommendation policy. PAR problem is usually tackled by scalable \emph{contextual bandit} algorithms, where the policies are generally based on classifiers. A practical problem in PAR is extreme click sparsity, due to very few users actually clicking on ads. We systematically study the drawback of using contextual bandit algorithms based on classifier-based policies, in face of extreme click sparsity. We then suggest an alternate policy, based on rankers, learnt by optimizing the Area Under the Curve (AUC) ranking loss, which can significantly alleviate the problem of click sparsity. We conduct extensive experiments on public datasets, as well as three industry proprietary datasets, to illustrate the improvement in click-through-rate (CTR) obtained by using the ranker-based policy over classifier-based policies.

Generalization error bounds for learning to rank: Does the length of document lists matter?

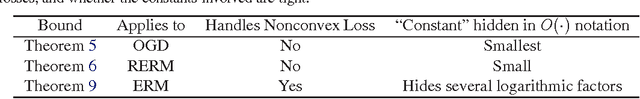
We consider the generalization ability of algorithms for learning to rank at a query level, a problem also called subset ranking. Existing generalization error bounds necessarily degrade as the size of the document list associated with a query increases. We show that such a degradation is not intrinsic to the problem. For several loss functions, including the cross-entropy loss used in the well known ListNet method, there is \emph{no} degradation in generalization ability as document lists become longer. We also provide novel generalization error bounds under $\ell_1$ regularization and faster convergence rates if the loss function is smooth.

Online Learning to Rank with Feedback at the Top

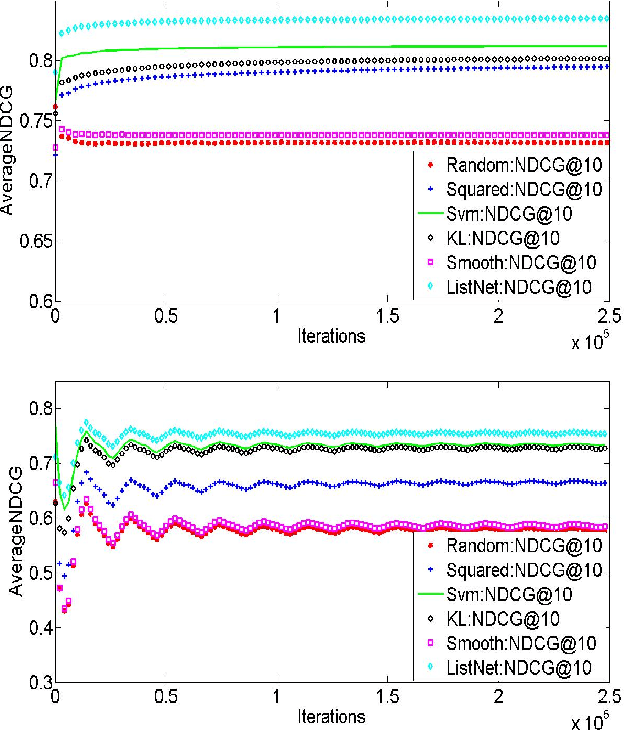
We consider an online learning to rank setting in which, at each round, an oblivious adversary generates a list of $m$ documents, pertaining to a query, and the learner produces scores to rank the documents. The adversary then generates a relevance vector and the learner updates its ranker according to the feedback received. We consider the setting where the feedback is restricted to be the relevance levels of only the top $k$ documents in the ranked list for $k \ll m$. However, the performance of learner is judged based on the unrevealed full relevance vectors, using an appropriate learning to rank loss function. We develop efficient algorithms for well known losses in the pointwise, pairwise and listwise families. We also prove that no online algorithm can have sublinear regret, with top-1 feedback, for any loss that is calibrated with respect to NDCG. We apply our algorithms on benchmark datasets demonstrating efficient online learning of a ranking function from highly restricted feedback.