Generalization error bounds for learning to rank: Does the length of document lists matter?
Paper and Code
Mar 06, 2016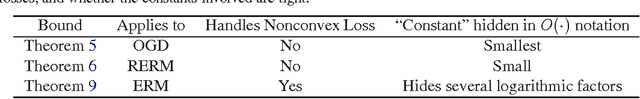
We consider the generalization ability of algorithms for learning to rank at a query level, a problem also called subset ranking. Existing generalization error bounds necessarily degrade as the size of the document list associated with a query increases. We show that such a degradation is not intrinsic to the problem. For several loss functions, including the cross-entropy loss used in the well known ListNet method, there is \emph{no} degradation in generalization ability as document lists become longer. We also provide novel generalization error bounds under $\ell_1$ regularization and faster convergence rates if the loss function is smooth.
* ICML 2015, volume 37 of JMLR Workshop and Conference Proceedings,
pg.- 315-323, 2015 * Appeared in ICML 2015. arXiv admin note: substantial text overlap
with arXiv:1405.0586
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge