Perceptron like Algorithms for Online Learning to Rank
Paper and Code
Aug 23, 2016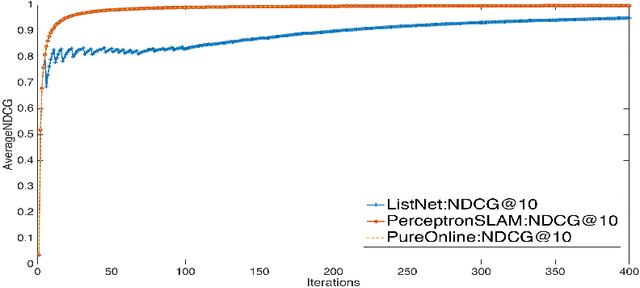
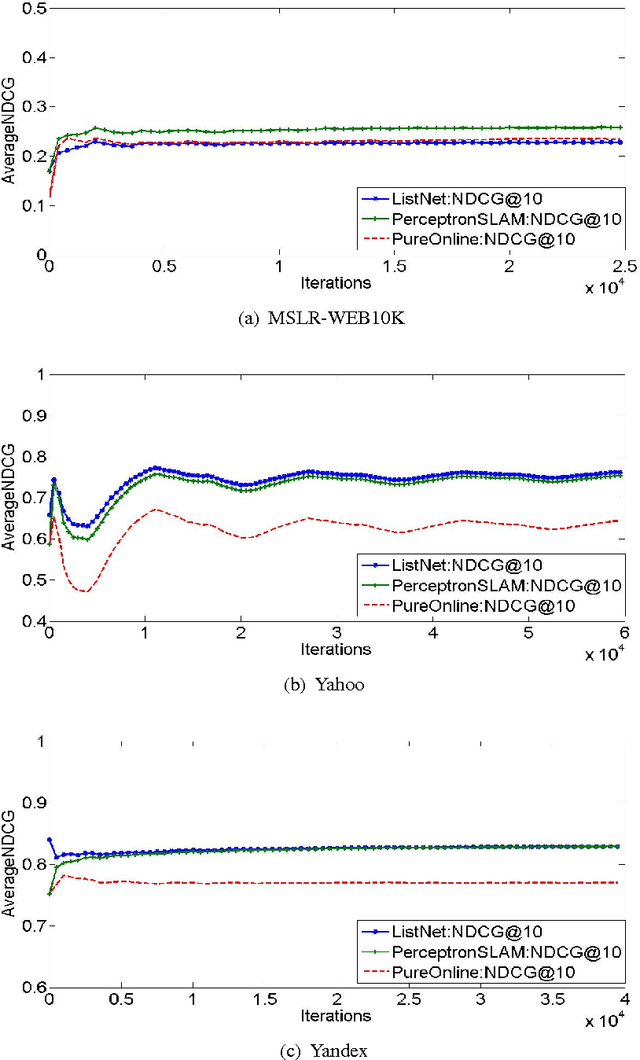
Perceptron is a classic online algorithm for learning a classification function. In this paper, we provide a novel extension of the perceptron algorithm to the learning to rank problem in information retrieval. We consider popular listwise performance measures such as Normalized Discounted Cumulative Gain (NDCG) and Average Precision (AP). A modern perspective on perceptron for classification is that it is simply an instance of online gradient descent (OGD), during mistake rounds, using the hinge loss function. Motivated by this interpretation, we propose a novel family of listwise, large margin ranking surrogates. Members of this family can be thought of as analogs of the hinge loss. Exploiting a certain self-bounding property of the proposed family, we provide a guarantee on the cumulative NDCG (or AP) induced loss incurred by our perceptron-like algorithm. We show that, if there exists a perfect oracle ranker which can correctly rank each instance in an online sequence of ranking data, with some margin, the cumulative loss of perceptron algorithm on that sequence is bounded by a constant, irrespective of the length of the sequence. This result is reminiscent of Novikoff's convergence theorem for the classification perceptron. Moreover, we prove a lower bound on the cumulative loss achievable by any deterministic algorithm, under the assumption of existence of perfect oracle ranker. The lower bound shows that our perceptron bound is not tight, and we propose another, \emph{purely online}, algorithm which achieves the lower bound. We provide empirical results on simulated and large commercial datasets to corroborate our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge