Online Learning to Rank with Top-k Feedback
Paper and Code
Aug 23, 2016
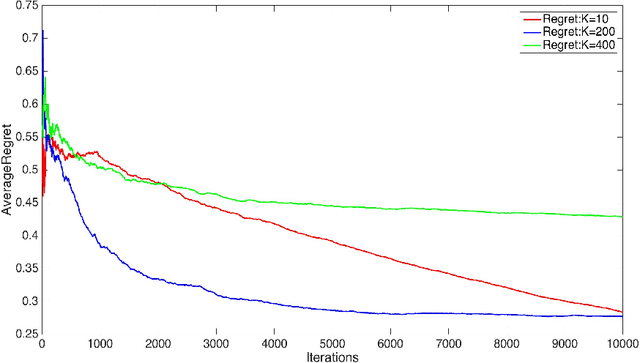
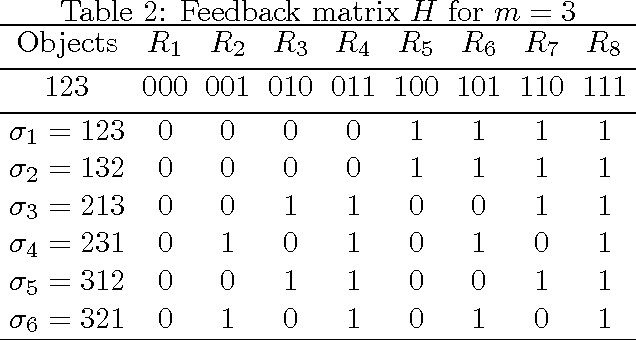
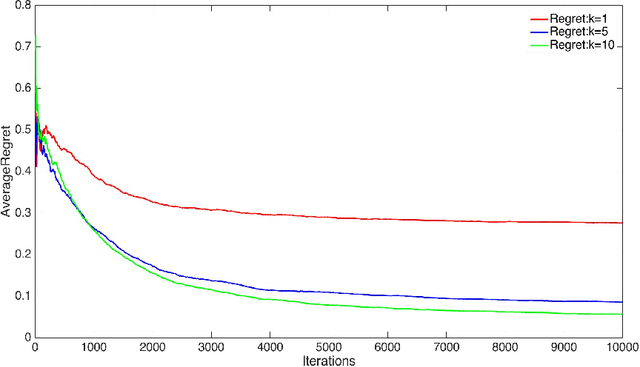
We consider two settings of online learning to rank where feedback is restricted to top ranked items. The problem is cast as an online game between a learner and sequence of users, over $T$ rounds. In both settings, the learners objective is to present ranked list of items to the users. The learner's performance is judged on the entire ranked list and true relevances of the items. However, the learner receives highly restricted feedback at end of each round, in form of relevances of only the top $k$ ranked items, where $k \ll m$. The first setting is \emph{non-contextual}, where the list of items to be ranked is fixed. The second setting is \emph{contextual}, where lists of items vary, in form of traditional query-document lists. No stochastic assumption is made on the generation process of relevances of items and contexts. We provide efficient ranking strategies for both the settings. The strategies achieve $O(T^{2/3})$ regret, where regret is based on popular ranking measures in first setting and ranking surrogates in second setting. We also provide impossibility results for certain ranking measures and a certain class of surrogates, when feedback is restricted to the top ranked item, i.e. $k=1$. We empirically demonstrate the performance of our algorithms on simulated and real world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge