Online Learning to Rank with Feedback at the Top
Paper and Code
Mar 06, 2016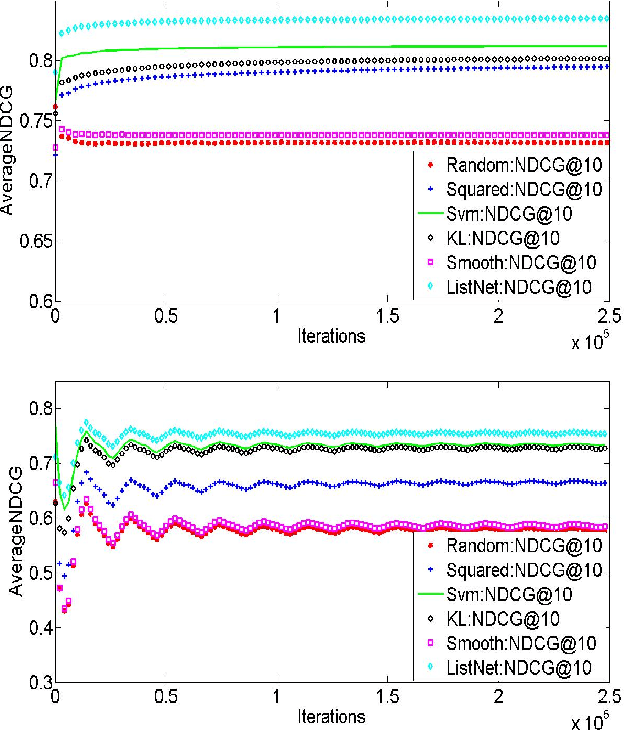

We consider an online learning to rank setting in which, at each round, an oblivious adversary generates a list of $m$ documents, pertaining to a query, and the learner produces scores to rank the documents. The adversary then generates a relevance vector and the learner updates its ranker according to the feedback received. We consider the setting where the feedback is restricted to be the relevance levels of only the top $k$ documents in the ranked list for $k \ll m$. However, the performance of learner is judged based on the unrevealed full relevance vectors, using an appropriate learning to rank loss function. We develop efficient algorithms for well known losses in the pointwise, pairwise and listwise families. We also prove that no online algorithm can have sublinear regret, with top-1 feedback, for any loss that is calibrated with respect to NDCG. We apply our algorithms on benchmark datasets demonstrating efficient online learning of a ranking function from highly restricted feedback.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge