Online Ranking with Top-1 Feedback
Paper and Code
Mar 06, 2016
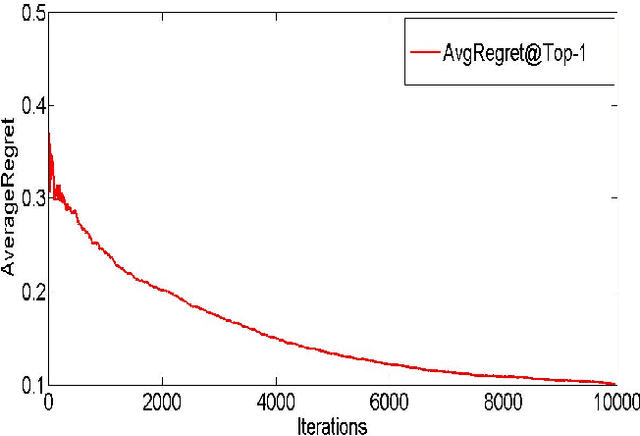

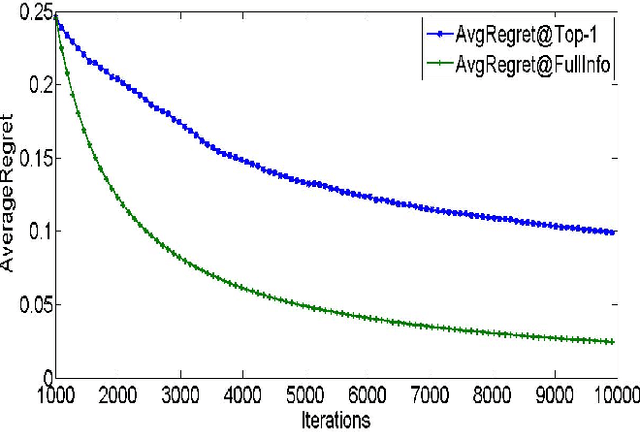
We consider a setting where a system learns to rank a fixed set of $m$ items. The goal is produce good item rankings for users with diverse interests who interact online with the system for $T$ rounds. We consider a novel top-$1$ feedback model: at the end of each round, the relevance score for only the top ranked object is revealed. However, the performance of the system is judged on the entire ranked list. We provide a comprehensive set of results regarding learnability under this challenging setting. For PairwiseLoss and DCG, two popular ranking measures, we prove that the minimax regret is $\Theta(T^{2/3})$. Moreover, the minimax regret is achievable using an efficient strategy that only spends $O(m \log m)$ time per round. The same efficient strategy achieves $O(T^{2/3})$ regret for Precision@$k$. Surprisingly, we show that for normalized versions of these ranking measures, i.e., AUC, NDCG \& MAP, no online ranking algorithm can have sublinear regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge